[题解] Codeforces Round 976 (Div. 2) A ~ E
A. Find Minimum Operations
签到.
void solve() {int n, k;cin >> n >> k;if (k == 1) {cout << n << endl;return;}int ans = 0;while (n) {ans += n % k;n /= k;}cout << ans << endl;
}
B. Brightness Begins
打表发现, 翻转完后的序列为: 011011110111111011111111. 每组 3 , 5 , 7 , 9... 3,5,7,9... 3,5,7,9... 个数.
直接用等差数列公式求出前缀中 1 1 1 的个数, 二分 check 答案
(赛时代码, 也不知道炸不炸 ll, 反正无脑套 __int128)
#define int long long
#define i128 __int128i128 f(i128 x) { // 求 x 组前缀中 1 的个数return ((2 * x + 1) + 3) * x / 2 - x;
}
i128 ff(i128 x) { // 求 x 组前缀中0和1的个数return ((2 * x + 1) + 3) * x / 2;
}
int solve(int _) {int k; cin >> k;i128 l = 0, r = 1e9;while (l < r) {int mid = (l + r + 1) >> 1;if (f(mid) > k)r = mid - 1;else if (f(mid) < k)l = mid;else return ff(mid);}return ff(l) + k - f(l) + 1;
}
C. Bitwise Balancing
先列出 a, b, c, d 每 bit 位的运算结果:
eg; fk, 赛时这个表画错了, 半天才发现
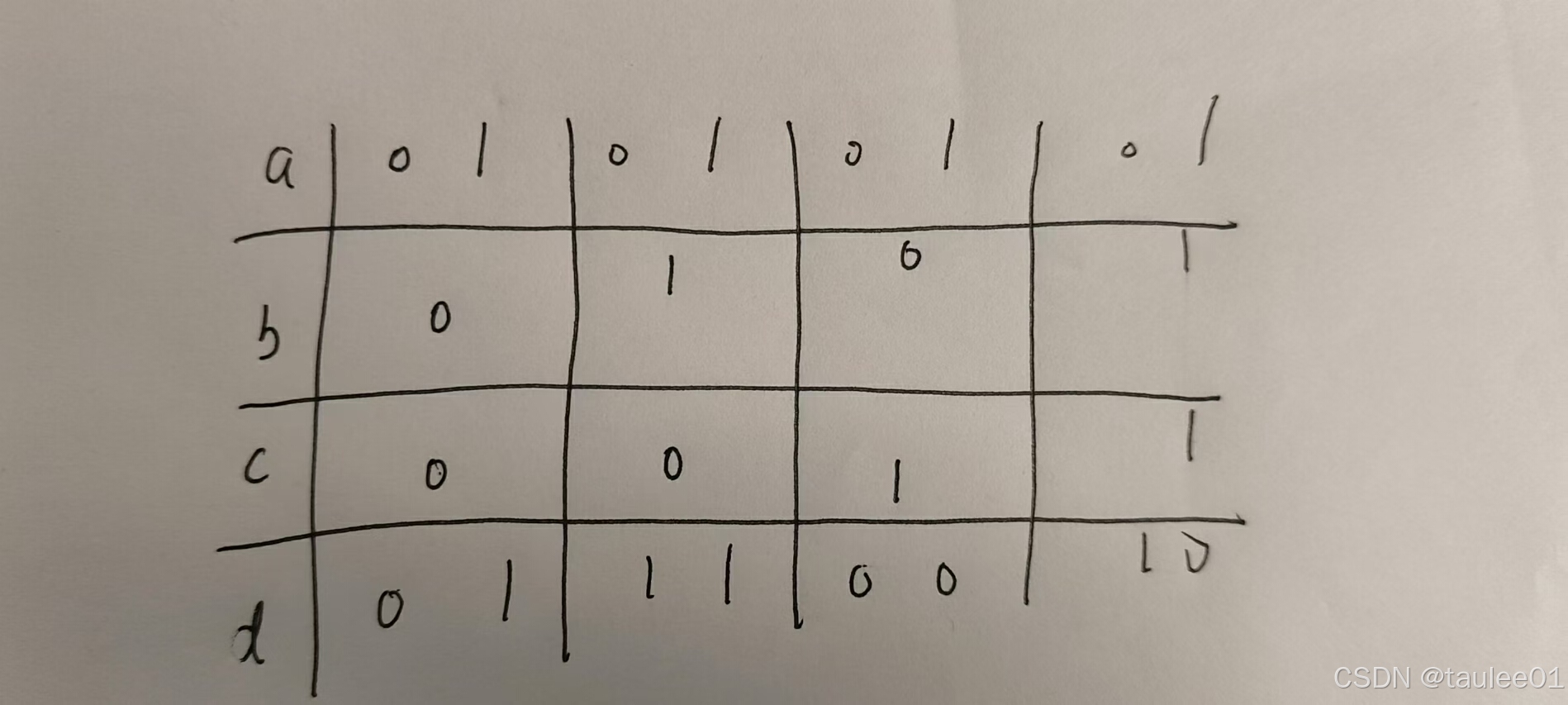
发现, 运算结果不会有负数. 于是每位就自能顾得上自己, 只需要按位检查, 一旦有一位满足不了, 就输出 -1.
#define int long longbool aa(int x, int i) {return (x >> i) & 1;}
int solve(int _) {int a, b, c, d;cin >> b >> c >> d;a = 0;for (int i = 0; i < 61; ++i) {if (aa(b, i)) {if (aa(c, i)) { //11if (!aa(d, i)) {a += 1ll << i;;}}else { // 10if (aa(d, i)) {a += 1ll << i;}else {return -1;}}}else {if (aa(c, i)) { // 01if (aa(d, i)) {return -1;}}else { // 00if (aa(d, i)) {a += 1ll << i;}}}}return a;
}
D. Connect the Dots
首先考虑用并查集维护两个点的连通块所属关系. 但是操作太多, 会 tle.
d 最大为 10, 于是对于 a[i], 考虑继承前 10 个节点往后跳跃的情况, 更新到 a[i] 上, 同时继承过来的跳跃次数减一. 这样每个点只用往前跳跃最多 10 次.
int n, m, a, d, k, fa[200010], ma[200010][15];
int find(int x) {if (fa[x] == x)return x;return fa[x] = find(fa[x]); //并查集路径压缩
}
int solve(int _) {cin >> n >> m;for (int i = 1; i <= n; ++i) {fa[i] = i;for (int j = 1; j <= 10; ++j) {ma[i][j] = 0;}}for (int i = 1; i <= m; ++i) {cin >> a >> d >> k;ma[a][d] = max(ma[a][d], k);}for (int i = 1; i <= n; ++i) {for (int j = 1; j <= 10; ++j) {if (i - j < 1)break;if (ma[i - j][j])fa[find(i)] = find(i - j); //从前面跳过来, 更新一下并查集}for (int j = 1; j <= 10; ++j) {if (ma[i][j] > 1 && i + j <= n)ma[i + j][j] = max(ma[i + j][j], ma[i][j] - 1); //继承全面没跳跃完的 k}}set<int>se;for (int i = 1; i <= n; ++i) {se.emplace(find(i));}return se.size();
}
E. Expected Power
状压 DP.
a 最大为 1023. 故所有数的异或结果最多 0~1023, 共 1024 种状态.
dp[i][j] 表示前 i 位选取某些异或到一起答案是 j 的概率. 就很好转移了. 见代码. 记得滚动数组优化一下空间.
eg: jiangly 的取模机真好用 ! !
eg: 赛后过题真痛苦, 就差几分钟…
//------取模机------//
using i64 = long long;
template<class T>
constexpr T power(T a, i64 b) {T res {1};for (; b; b /= 2, a *= a) {if (b % 2) {res *= a;}}return res;
} // 快速幂constexpr i64 mul(i64 a, i64 b, i64 p) {i64 res = a * b - i64(1.L * a * b / p) * p;res %= p;if (res < 0) {res += p;}return res;
} // 取模乘template<i64 P>
struct MInt {i64 x;constexpr MInt() : x {0} {}constexpr MInt(i64 x) : x {norm(x % getMod())} {}static i64 Mod;constexpr static i64 getMod() {if (P > 0) {return P;} else {return Mod;}}constexpr static void setMod(i64 Mod_) {Mod = Mod_;}//只有P<=0, setMod才生效constexpr i64 norm(i64 x) const {if (x < 0) {x += getMod();}if (x >= getMod()) {x -= getMod();}return x;}constexpr i64 val() const {return x;}constexpr MInt operator-() const {MInt res;res.x = norm(getMod() - x);return res;}constexpr MInt inv() const {return power(*this, getMod() - 2);}constexpr MInt &operator*=(MInt rhs) & {if (getMod() < (1ULL << 31)) {x = x * rhs.x % int(getMod());} else {x = mul(x, rhs.x, getMod());}return *this;}constexpr MInt &operator+=(MInt rhs) & {x = norm(x + rhs.x);return *this;}constexpr MInt &operator-=(MInt rhs) & {x = norm(x - rhs.x);return *this;}constexpr MInt &operator/=(MInt rhs) & {return *this *= rhs.inv();}friend constexpr MInt operator*(MInt lhs, MInt rhs) {MInt res = lhs;res *= rhs;return res;}friend constexpr MInt operator+(MInt lhs, MInt rhs) {MInt res = lhs;res += rhs;return res;}friend constexpr MInt operator-(MInt lhs, MInt rhs) {MInt res = lhs;res -= rhs;return res;}friend constexpr MInt operator/(MInt lhs, MInt rhs) {MInt res = lhs;res /= rhs;return res;}friend constexpr std::istream &operator>>(std::istream &is, MInt &a) {i64 v;is >> v;a = MInt(v);return is;}friend constexpr std::ostream &operator<<(std::ostream &os, const MInt &a) {return os << a.val();}friend constexpr bool operator==(MInt lhs, MInt rhs) {return lhs.val() == rhs.val();}friend constexpr bool operator!=(MInt lhs, MInt rhs) {return lhs.val() != rhs.val();}friend constexpr bool operator<(MInt lhs, MInt rhs) {return lhs.val() < rhs.val();}
};template<>
i64 MInt<0>::Mod = 1e9 + 7; //只有P<=0, Mod才生效constexpr int P = 1e9 + 7; //在这设置要用的模数
using Z = MInt<P>;
//------取模机------//i64 n, a[200010];
Z dp[2][1024], p[200010];
int solve(int _) {cin >> n;for (int i = 1; i <= n; ++i) cin >> a[i];for (int i = 1; i <= n; ++i) {cin >> p[i]; p[i] /= 1e4;}Z ans = 0;dp[0][0] = 1;for (int i = 1; i < 1024; ++i) {dp[0][i] = 0;}for (int i = 1; i <= n; ++i) {int tis = i % 2;int last = tis ^ 1;for (int j = 0; j < 1024; ++j) dp[tis][j] = 0;for (int j = 0; j < 1024; ++j) {dp[tis][j ^ a[i]] += dp[last][j] * p[i];dp[tis][j] += dp[last][j] * (1 - p[i]);}}for (int i = 0; i < 1024; ++i) {ans += dp[n % 2][i] * i * i;}return ans.val();
}
相关文章:

[题解] Codeforces Round 976 (Div. 2) A ~ E
A. Find Minimum Operations 签到. void solve() {int n, k;cin >> n >> k;if (k 1) {cout << n << endl;return;}int ans 0;while (n) {ans n % k;n / k;}cout << ans << endl; }B. Brightness Begins 打表发现, 翻转完后的序列为: 0…...
【零基础入门产品经理】学习准备篇 | 需要学一些什么呢?
前言: 零实习转行产品经理经验分享01-学习准备篇_哔哩哔哩_bilibili 该篇内容主要是对bilibili这个视频的观后笔记~谢谢美丽滴up主友情分享。 全文摘要:如何在0实习且没有任何产品相关经验下,如何上岸产品经理~ 目录 一、想清楚为什么…...

第四届机器人、自动化与智能控制国际会议(ICRAIC 2024)征稿
第四届机器人、自动化与智能控制国际会议(ICRAIC 2024)由湖南第一师范学院主办,南京师范大学、山东女子学院、爱迩思出版社(ELSP)协办。 大会将专注于机器人、数字化、自动化、人工智能等技术的开发和融合,…...
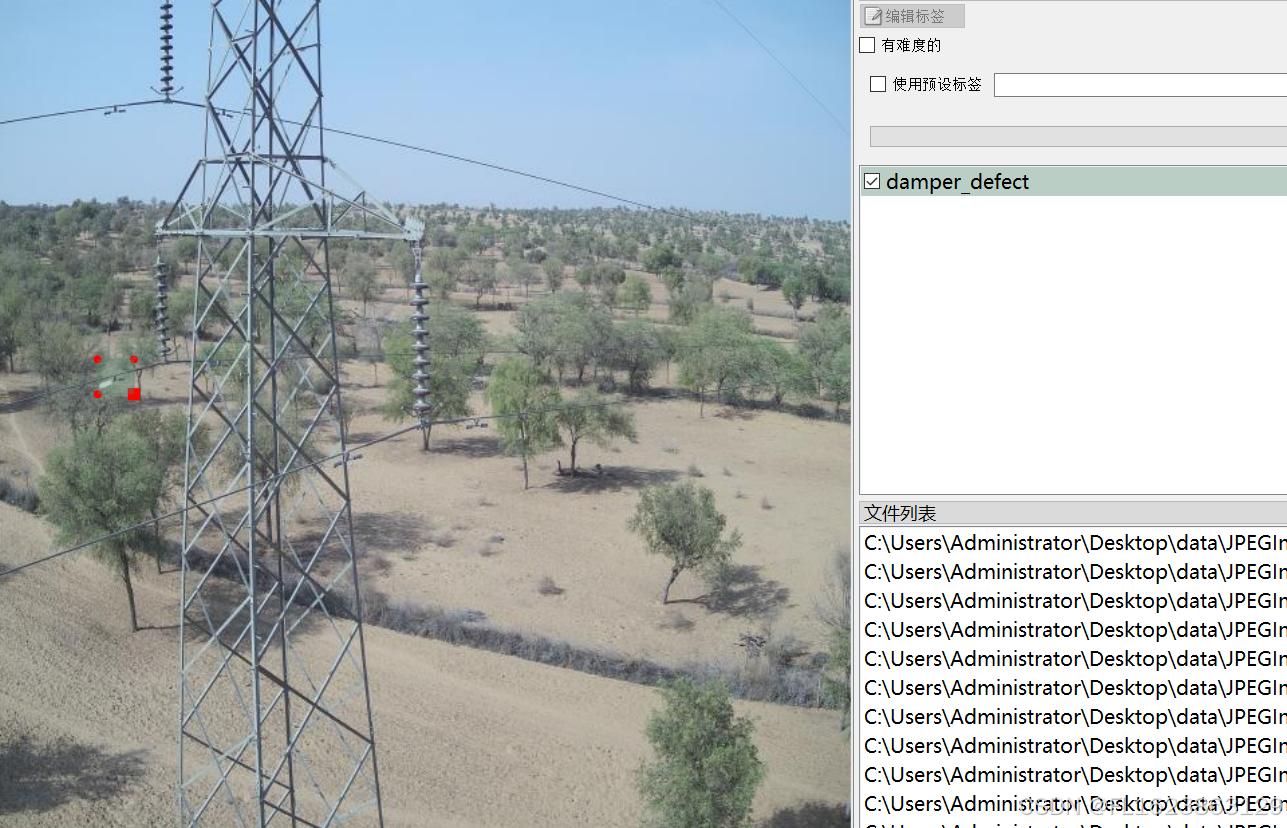
[数据集][目标检测]电力场景防震锤缺陷检测数据集VOC+YOLO格式705张1类别
重要说明:防震锤缺陷图片太难找,数据集里面存在大量单一场景图片,请仔细查看图片预览谨慎下载,此外数据集均为小目标检测,如果训练map偏低属于正常现象 数据集格式:Pascal VOC格式YOLO格式(不包含分割路径…...

【SpringBoot】
目录 一、Spring Boot概要 1. SpringBoot介绍 2. SpringBoot优点 3. SpringBoot缺点 4. 时代背景-微服务 二、Spring Boot 核心配置 1. Spring Boot配置文件分类 1.1 application.properties 1.2 application.yml 1.3 小结 2. YAML概述 3. YAML基础语法 3.1 注意事…...
Linux操作系统中MongoDB
1、什么是MongoDB 1、非关系型数据库 NoSQL,泛指非关系型的数据库。随着互联网web2.0网站的兴起,传统的关系数据库在处理web2.0网站,特别是超大规模和高并发的SNS类型的web2.0纯动态网站已经显得力不从心,出现了很多难以克服的问…...

2、.Net 前端框架:OpenAuth.Net - .Net宣传系列文章
OpenAuth.Net 是一个开源的身份验证框架,由开发者 Yubaolee 创建,它旨在简化 Web 应用和服务的安全授权过程。这个框架以其强大的功能和易用性,为开发人员提供了一种高效的方式来处理用户认证和授权问题。 OpenAuth.Net 的关键特性包括&#…...
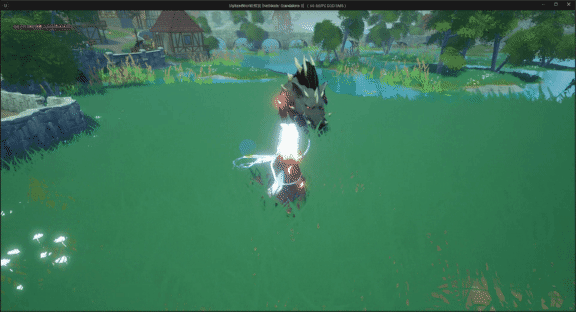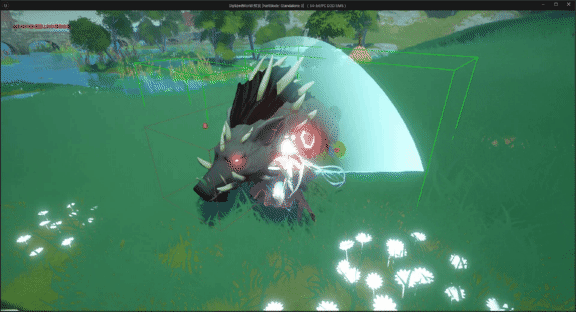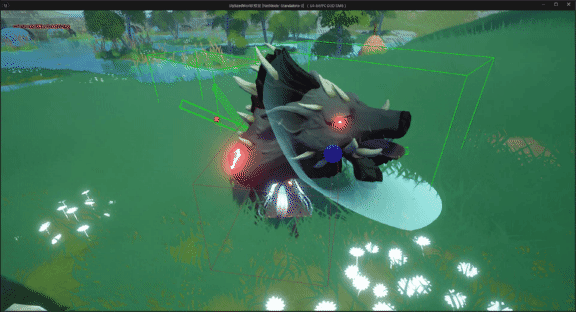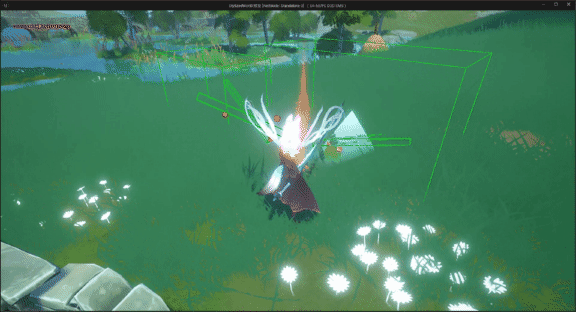
unreal engine5制作动作类游戏时,我们使用刀剑等武器攻击怪物或敌方单位时,发现攻击特效、伤害等没有触发
UE5系列文章目录 文章目录 UE5系列文章目录前言一、问题分析二、解决方法1. 添加项目设置碰撞检测通道2.玩家角色碰撞设置3.怪物角色碰撞预设 最终效果 前言 在使用unreal engine5制作动作类游戏时,我们使用刀剑等武器攻击怪物或敌方单位时,发现攻击特效…...
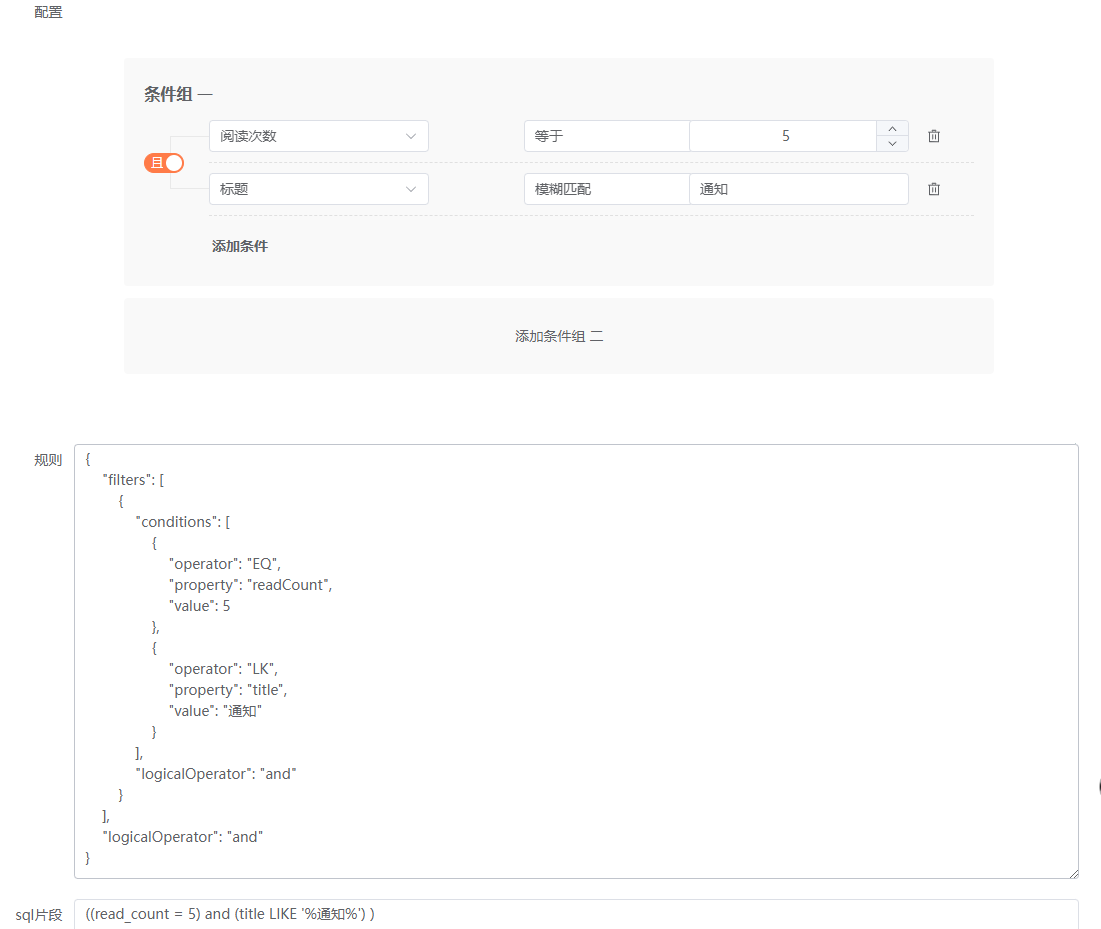
数据权限的设计与实现系列11——前端筛选器组件Everright-filter集成功能完善2
筛选条件数据类型完善 文本类 筛选器组件给了一个文本类操作的范例,如下: Text: [{label: 等于,en_label: Equal,style: noop},{label: 等于其中之一,en_label: Equal to one of,value: one_of,style: tags},{label: 不等于,en_label: Not equal,v…...

C++ 游戏开发
C游戏开发 C 是一种高效、灵活且功能强大的编程语言,因其性能和控制能力而在游戏开发中被广泛应用。许多著名的游戏引擎,如 Unreal Engine、CryEngine 和 Godot 等,都依赖于 C 进行核心开发。本文将详细介绍 C 在游戏开发中的应用࿰…...
)
【历年CSP-S复赛第一题】暴力解法与正解合集(2019-2022)
P5657 [CSP-S2019] 格雷码P7076 [CSP-S2020] 动物园P7913 [CSP-S 2021] 廊桥分配P8817 [CSP-S 2022] 假期计划 P5657 [CSP-S2019] 格雷码 暴力50分 #include<bits/stdc.h> #define IOS ios::sync_with_stdio(false),cin.tie(0),cout.tie(0) #define int long long #d…...

基于PyQt5和SQLite的数据库操作程序
基于PyQt5和SQLite的数据库操作程序:功能解析 在现代办公和数据处理中,数据库操作是不可或缺的一部分。然而,传统的数据库管理工具往往界面复杂,操作繁琐,对于非专业人士来说存在一定的学习曲线。为了解决这个问题,我们开发了一款基于PyQt5和SQLite的数据库操作程序。该…...
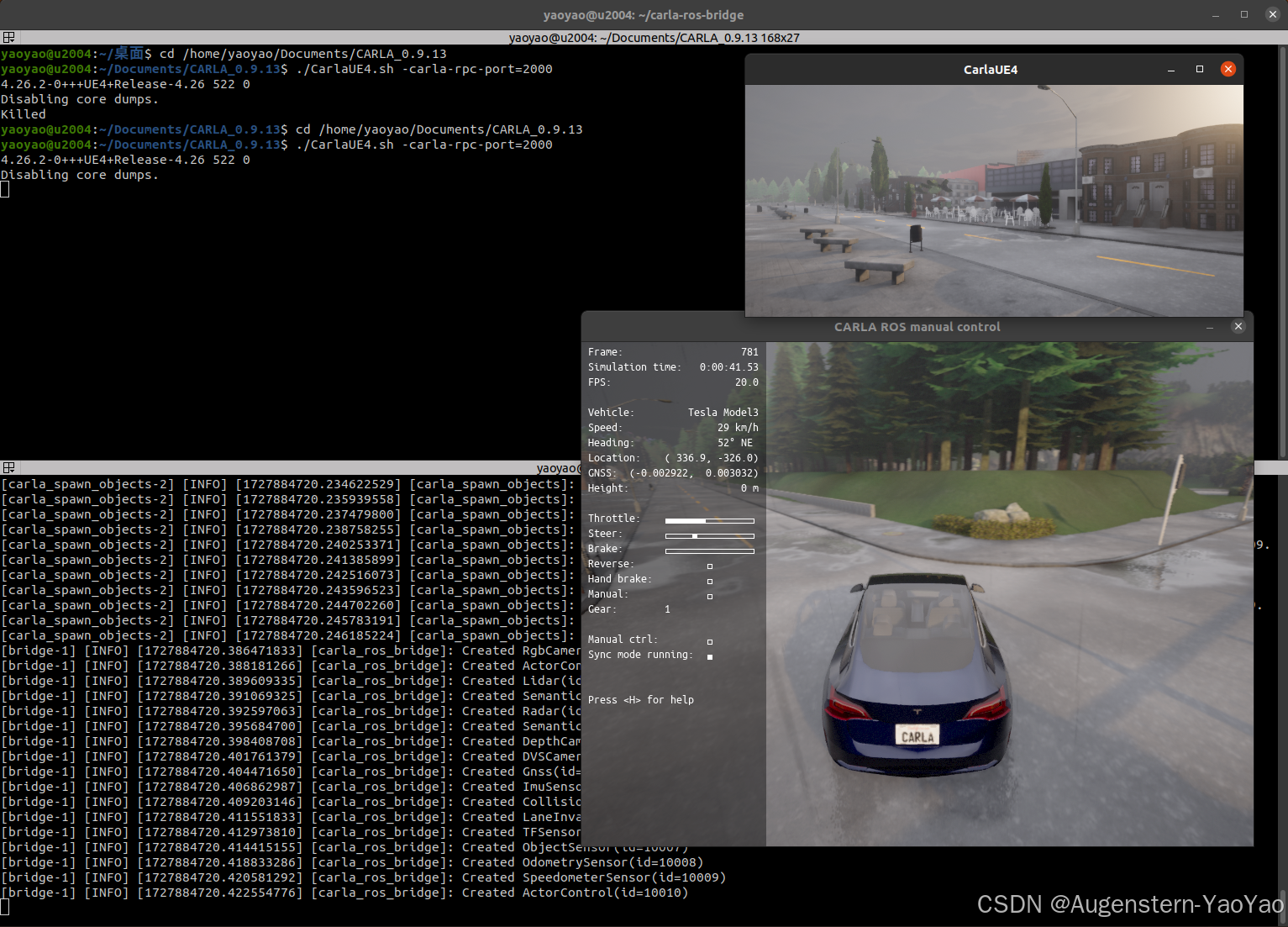
在Ubuntu 20.04中安装CARLA
0. 引言 CARLA (Car Learning to Act) 是一款开源自动驾驶模拟器,其支持自动驾驶系统全管线的开发、训练和验证(Development, Training, and Validation of autonomous driving systems)。Carla提供了丰富的数字资产,例如城市布局…...
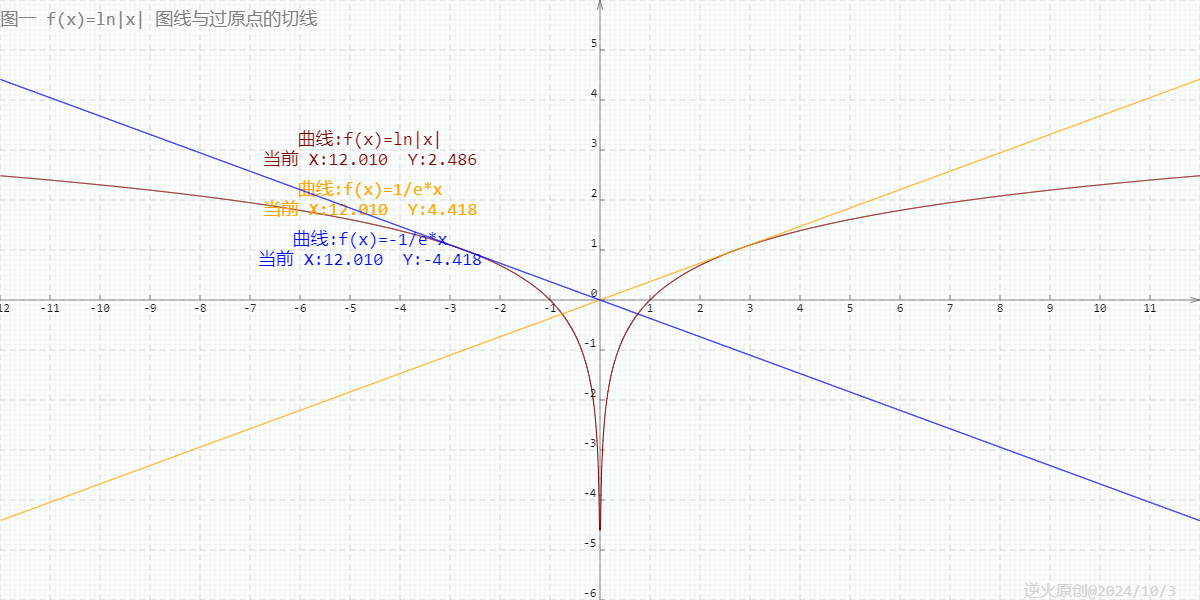
【高中数学/对数/导数】曲线y=ln|x|过坐标原点的两切线方程为?
【问题】 曲线yln|x|过坐标原点的两切线方程为?(高考真题) 【出处】 《高考数学 函数与导数题型解题研究》P5第8题 中原教研工作室编著 【解答】 yln|x|的图线分两部分,y轴左边的部分是ylnx的镜像 所以知ylnx上切线过原点的…...

Qt CMake
使用 CMake 构建 CMake 是一款用于简化跨不同平台开发项目的构建流程的工具。 CMake 可自动生成构建系统,如 Makefile 和 Visual Studio 项目文件。 CMake 是一个第三方工具,有自己的文档。 本主题介绍如何在 Qt 5 中使用 CMake 3.1.0。 开始使用 CMak…...
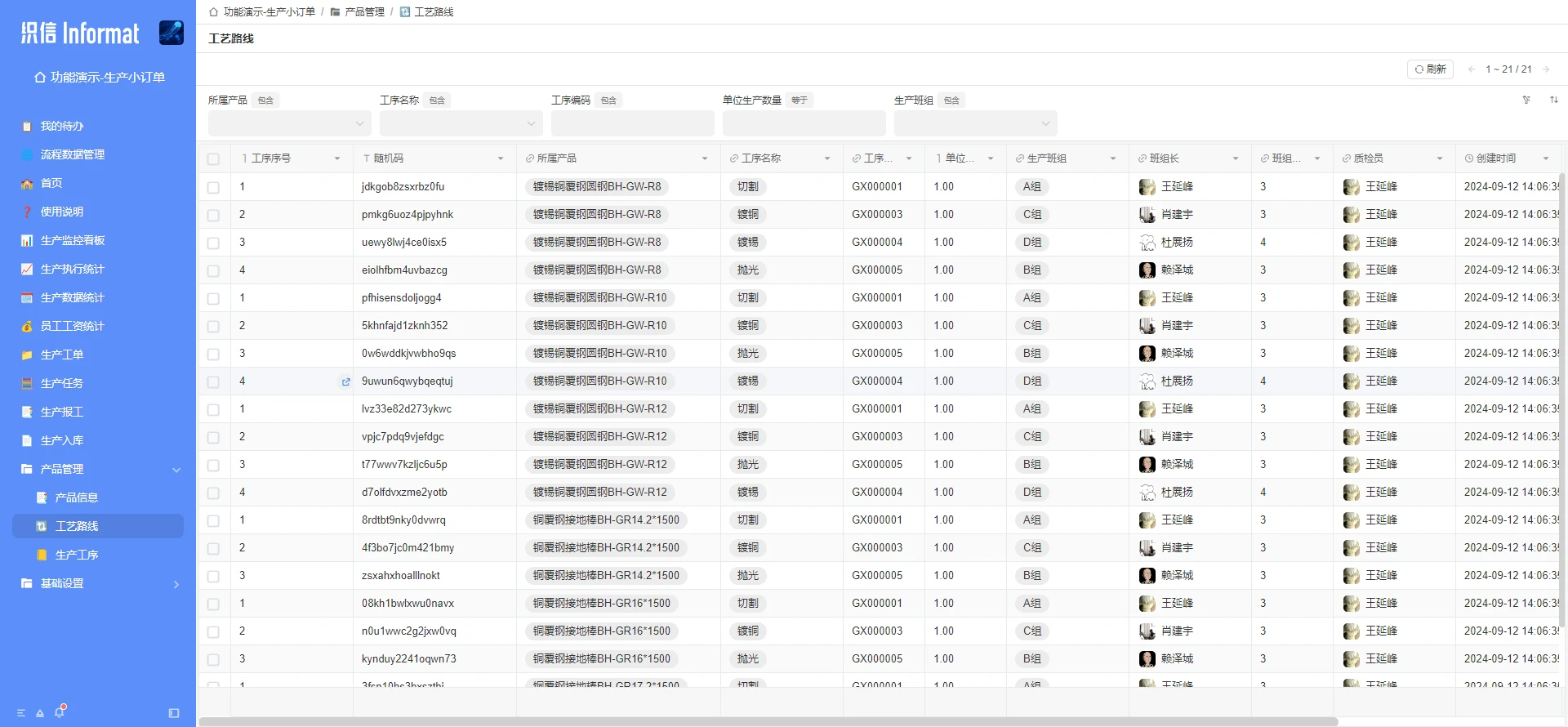
制造企业各部门如何参与生产成本控制与管理?
国内制造业的分量可不轻,从日常生活用品到高端工业设备,中国制造几乎涵盖了各个领域。 不过很多制造业企业在管理方面确实存在一些难题:成本控制不容易,产品质量并不稳定,生产周期也常常较长。 一、中国制造业生产管…...
FireRedTTS - 小红书最新开源AI语音克隆合成系统 免训练一键音频克隆 本地一键整合包下载
小红书技术团队FireRed最近推出了一款名为FireRedTTS的先进语音合成系统,该系统能够基于少量参考音频快速模仿任意音色和说话风格,实现独特的音频内容创造。 FireRedTTS 只需要给定文本和几秒钟参考音频,无需训练,就可模仿任意音色…...
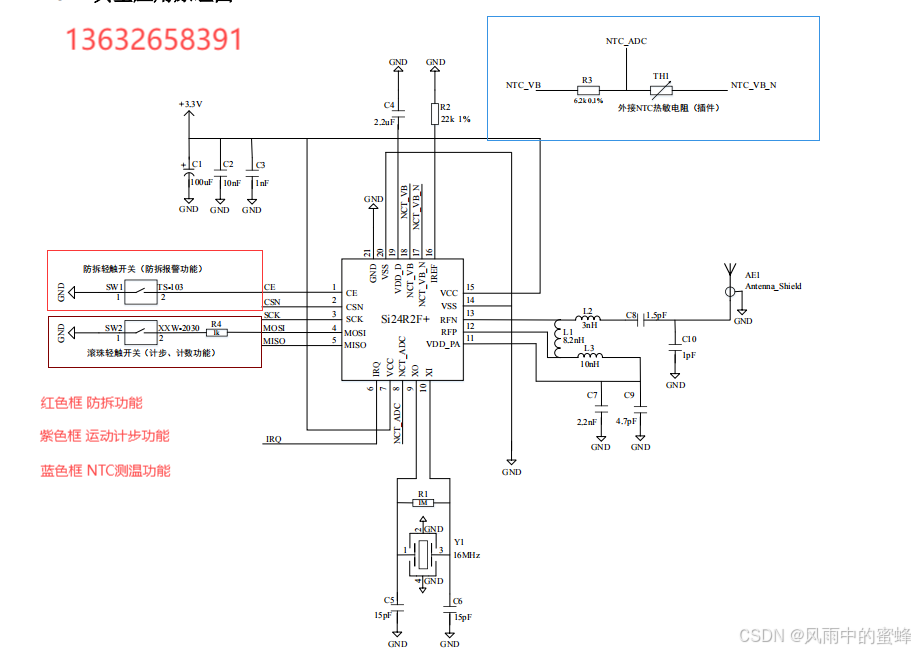
活体检测标签之2.4G有源RFID--SI24R2F+
首先从客户对食品安全和可追溯性的关注切入,引出活体标签这个解决方案。接着分别阐述活体标签在动物养殖和植物产品方面的应用,强调其像 “身份证” 一样记录重要信息,让客户能够了解食品的来源和成长历程,从而放心食用。最后呼吁…...
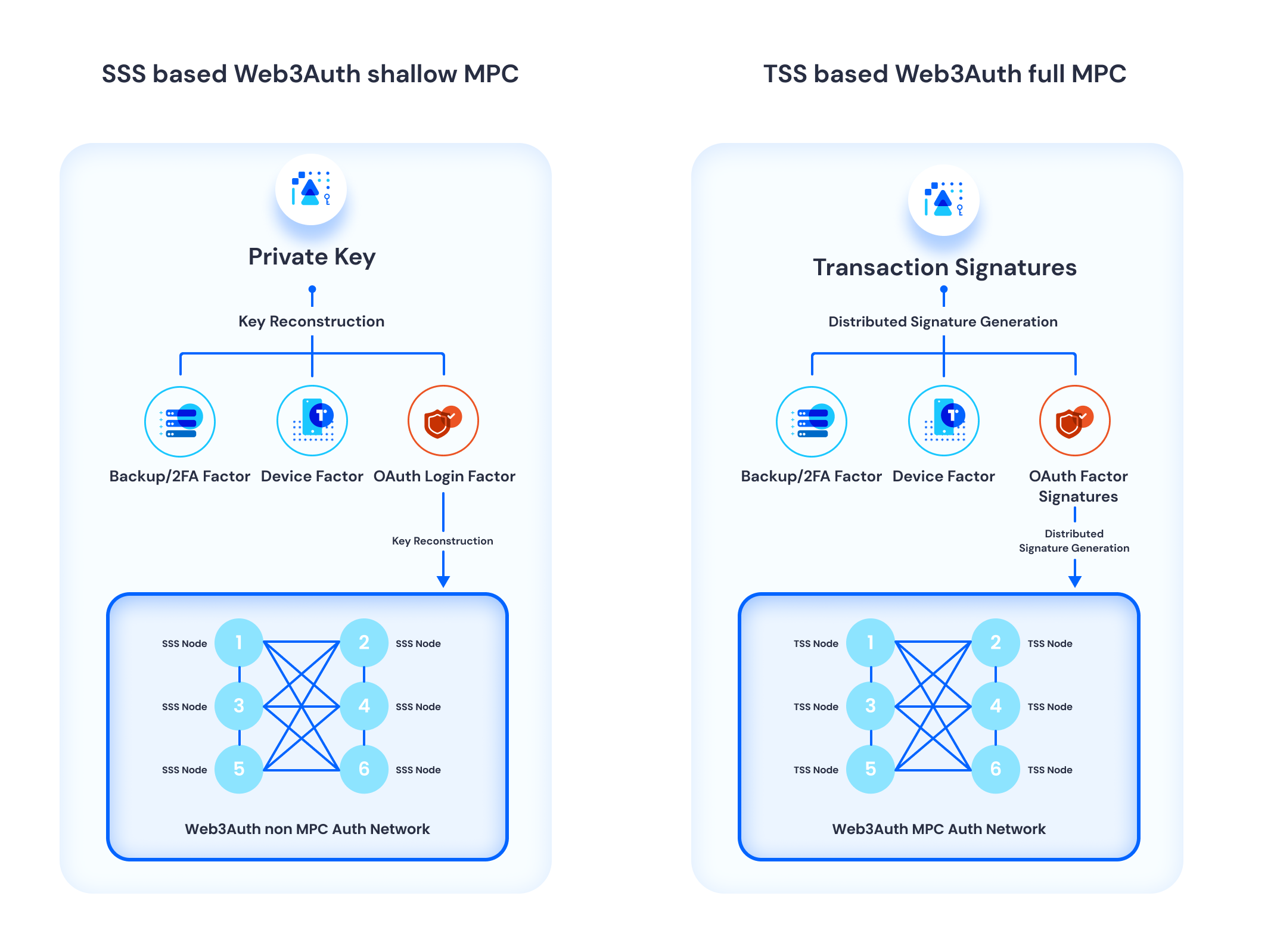
Web3Auth 如何工作?
Web3Auth 用作钱包基础设施,为去中心化应用程序 (dApp) 和区块链钱包提供增强的灵活性和安全性。在本文档中,我们将探索 Web3Auth 的功能,展示它如何为每个用户和应用程序生成唯一的加密密钥提供程序。 高级架构 Web3Auth SDK 完全存在于用…...

问:SQL中join语法的差异?
在SQL中,JOIN语法用于结合来自两个或多个表的数据。不同类型的JOIN会基于不同的条件来合并表中的数据。以下是几种常见的JOIN及其差异: 假设我们有两个表:employees 和 departments。 employees 表: employee_idnamedepartment_id1Alice10…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...
