常见排序算法以及冒泡排序的基础使用方法
众所周知,冒泡排序是编程中最经典也是最简单的一种排序方法,它是通过重复访问对两个相邻的值进行比较,由于在互换的过程中,最大 (或最小) 的那个值会慢慢的交换到顶部,像汽水一样,故名“冒泡排序”。
-
let arr = [3,9,5,1,8,2,14,10]//arr的长度为8,需要确定7个值,外循环arr.length- 1 for(let i = 0; i < arr.length - 1; i++) { for(let j = 0;j < arr.length - 1 - i;j++){//第一轮循环,需要对比6次,内循环arr.length - 1 -i if (arr[j] > arr[j+1]){ let num = arr[j]; arr[j] = arr[j+1]; arr[j+1] = num; } } } console.log(arr); // 最终结果:1 2 3 5 8 9 10 14冒泡比较消耗性能,因为说白了他是将一个数字与所有数字都进行一次比较,然后来确定位置,在进行下一个数字与所有数字进行比较,所以经常不建议使用.
毕竟排序的方法有多种:1.冒泡排序
算法描述
比较相邻的元素。如果第一个比第二个大,就交换它们两个;
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
针对所有的元素重复以上的步骤,除了最后一个;
重复步骤1~3,直到排序完成2.选择排序
算法分析
表现最稳定的排序算法之一,因为无论什么数据进去都是O(n2)的时间复杂度,所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。理论上讲,选择排序可能也是平时排序一般人想到的最多的排序方法了吧3.插入排序
算法分析
插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间4.归并排序
算法分析
归并排序是一种稳定的排序方法。和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(nlogn)的时间复杂度。代价是需要额外的内存空间5.快速排序
算法描述
快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。具体算法描述如下:
从数列中挑出一个元素,称为 “基准”(pivot) ; (相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序我就不一一列举了,常用的排序方法还有“希尔排序”,“堆排序”,“计数排序”,“桶排序”...
相关文章:

常见排序算法以及冒泡排序的基础使用方法
众所周知,冒泡排序是编程中最经典也是最简单的一种排序方法,它是通过重复访问对两个相邻的值进行比较,由于在互换的过程中,最大 (或最小) 的那个值会慢慢的交换到顶部,像汽水一样,故名“冒泡排序”。 let a…...
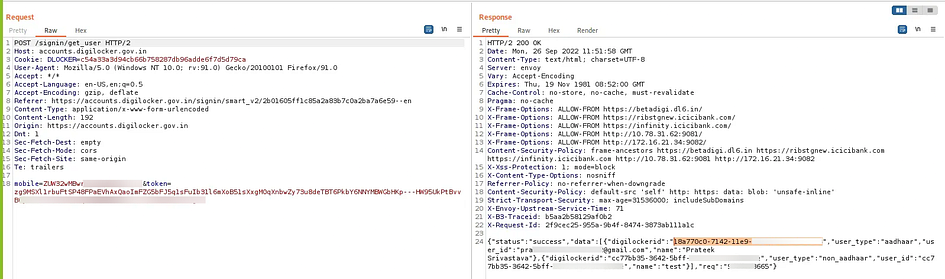
【网络安全】Cookie与ID未强绑定导致账户接管
未经许可,不得转载。 文章目录 前言正文前言 DigiLocker 是一项在线服务,旨在为公民提供一个安全的数字平台,用于存储和访问重要的文档,如 Aadhaar 卡、PAN 卡和成绩单等。DigiLocker 通过多因素身份验证(MFA)来保护用户账户安全,通常包括 6 位数的安全 PIN 和一次性密…...

Ansible Playbook原理与实践(Principles and Practice of Ansible Playbook)
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 本人主要分享计算机核心技…...

解决OpenCV保存视频 视频全部为绿色的bug
目录 项目场景: 问题描述 原因分析: 解决方案: 项目场景: 使用OpenCV-Python 保存视频,视频为numpy array格式,保存的视频全部为无意义的绿色。 问题描述 用opencv 保存的视频会出现全部为绿色的情况&…...

手机使用指南:如何在没有备份的情况下从 Android 设备恢复已删除的联系人
在本指南中,您将了解如何从 Android 手机内存中恢复已删除的联系人。Android 诞生、见证并征服了 80% 的智能手机行业。有些人可能将此称为“非常大胆的宣言”,但最近的统计数据完全支持我们的说法。灵活性、高度改进的可用性和快速性是 Android 操作系统…...
:函数)
TS系列(6):函数
你好,我是沐爸,欢迎点赞、收藏、评论和关注。 TS系列(1):TS是什么?如何使用? TS系列(2):类型声明、类型推断和类型总览 TS系列(3)&…...

网盘能否作为FTP替代产品?企业该如何进行FTP国产化替代?
近年来,信创的概念引入和高效实践落地让更多的行业企业自发性地进行国产化替代,目前信创国产化替代还多发生在操作系统和应用层面,软件工具等目前还在下一阶段规划,但很多企业未雨绸缪,已经在做调研和尝试。 FTP作为世…...

Python操作MongoDB
一、Python链接MongoDB 1、安装pymongo包 使用包管理器安装 pip3 insatll pymongo 2、连接MongoDB 首先需要导入pymongo包: from pymongo import MongoClient 创建MongoClient对象: from pymongo import MongoClient #创建MongoClient对象&#…...

Redis --- 第二讲 --- 特性和安装
一、背景知识 Redis特性: Redis是一个在内存中存储数据的中间件,用于作为数据库,作为缓存,在分布式系统中能够大展拳脚。Redis的一些特性造就了现在的Redis。 在内存中存储数据,通过一系列的数据结构。MySQL主要是通…...

基于单片机的两轮直立平衡车的设计
本设计基于单片机设计的两轮自平衡小车,其中机械部分包括车体、车轮、直流电机、锂电池等部件。控制电路板采用STC12C5A60S2作为主控制器,采用6轴姿态传感器MPU6050测量小车倾角,采用TB6612FNG芯片驱动电机。通过模块化编程完成了平衡车系统软…...

828华为云征文|部署个人知识管理系统 SiyuanNote
828华为云征文|部署个人知识管理系统 SiyuanNote 一、Flexus云服务器X实例介绍二、Flexus云服务器X实例配置2.1 重置密码2.2 服务器连接2.3 安全组配置2.4 Docker 环境搭建 三、Flexus云服务器X实例部署 SiyuanNote3.1 SiyuanNote 介绍3.2 SiyuanNote 部署3.3 Siyua…...

MATLAB中pcg函数用法
目录 语法 说明 示例 线性系统的迭代解 使用指定了预条件子的 pcg 提供初始估计值 使用函数句柄代替数值矩阵 pcg函数的功能是求解线性系统 - 预条件共轭梯度法。 语法 x pcg(A,b) x pcg(A,b,tol) x pcg(A,b,tol,maxit) x pcg(A,b,tol,maxit,M) x pcg(A,b,tol,ma…...

Veritus netbackup 管理控制台无法连接:未知错误
节假日停电,netbackup服务器意外停机后重新开机,使用netbackup管理控制台无法连接,提示未知错误。 ssh连接到服务器,操作系统正常,那应该是应用有问题,先试一下重启服务器看看。重新正常关机,重…...

安全中心 (SOC) 与 网络运营中心 (NOC)
NOC 和 SOC 之间的区别 网络运营中心 (NOC) 负责维护公司计算机系统的技术基础设施,而安全运营中心 (SOC) 则负责保护组织免受网络威胁。 NOC 专注于防止自然灾害、停电和互联网中断等自然原因造成的网络干扰,而 SOC 则从事监控、管理和保护。 NOC 提…...

WPS使用越来越卡顿
UOS统信wps频繁的使用后出现卡顿问题,通过删除或重命名kingsoft文件缓存目录。 文章目录 一、问题描述二、问题原因三、解决方案步骤一步骤二步骤三 一、问题描述 用户在频繁的使用wps处理工作,在使用一段时间后,用户反馈wps打开速度慢&…...

吴恩达深度学习笔记:卷积神经网络(Foundations of Convolutional Neural Networks)2.5-2.6
目录 第四门课 卷积神经网络(Convolutional Neural Networks)第二周 深度卷积网络:实例探究(Deep convolutional models: case studies)2.5 网络中的网络以及 11 卷积(Network in Network and 11 convoluti…...

C# 解决Excel边框样式无法复制问题及实现格式刷功能
目录 问题现象 范例运行环境 解决方案 剪贴板加特殊粘贴 自定义样式 直接赋值 完美方案 小结 问题现象 在运行数据表数据导出到 EXCEL 数据输出时遇到了一个问题,开发者设计了单行细线下边框的输出模板,如下图设计: 其中 <%syst…...

前端组件化开发
假设这个页面是vue开发的,如果一整个页面都是编写在一个vue文件里面,后期不好维护,会特别的庞大,那么如何这个时候需要进行组件化开发。组件化开发后必然会带来一个问题需要进行组件之间的通信。组要是父子组件之间通信࿰…...

异步操作实现线程池
文章目录 futureasyncpromisepackage task C11线程池实现 future 在C11标准库中,提供了一个future的模板类,它表示的是一个异步操作的结果,当在多线程编程中使用异步任务的时候,使用这个类可以帮助在需要的时候获取到对应的数据处…...

长期提供APX515/B原装二手APX525/B音频分析仪
Audio Precision APx515 是一款针对生产测试而优化的高性能音频分析仪。它因其速度、性能、自动化和易用性而成为一流的仪器。它具有卓越的性能,具有 –106 dB 的典型 THDN、1M 点 FFT 和 192k 数字 I/O,以及所有 APx 系列音频分析仪的一键式自动化和易用…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
