云计算SLA响应时间的matlab模拟与仿真
目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
5.完整程序
1.程序功能描述
用matlab模拟,一个排队理论。输入一堆包,经过buffer(一个或者几个都行)传给server,这些包会在buffer里面进行排队,采取FIFO的排序方法。

本课题用到了一个公式
q(t)=max(0,q(t-1)+a(t)-1)
意思是现在在buffer里面排队的数据包的个数 是等于 前一时间排队的数据包的个数加上新到达的数据包的个数,减去离开的也就是被处理的数据包的个数。值随时间变化。
在传输的过程中,要用Poisson Random Variable的公式生成随机的traffic。
最后输出的结果要求是q(t)的柱状图,主要结果是要比较最开始每个包之间的时间,和经过buffer还有traffic影响之后到达的每个包之间的时间差。
2.测试软件版本以及运行结果展示
MATLAB2022A版本运行








(完整程序运行后无水印)
3.核心程序
%绘制每一个时刻下,FIFO中的数据包的数量q(t)的函数变化
figure;
subplot(211);
bar(FIFO_DATA);
grid on;
legend('Q(t)整体显示效果');
axis([1,10000,0,1.2*max(FIFO_DATA)]);
title('显示某一次的仿真结果');
subplot(212);
bar(FIFO_DATA);
grid on;
legend('Q(t)局部显示效果');
axis([4000,4050,0,1.2*max(FIFO_DATA(4000:4050))]);
title('显示某一次的仿真结果');%比较最开始每个包之间的时间,和经过buffer还有traffic影响之后到达的每个包之间的时间差。
figure
plot(0:Num_FIFO_Package,[0 abs(Package_Infor(1,Package_Index)-Package_Infor(4,Package_Index))]);
ylabel('The time');
xlabel('The Package');
legend('时间差');
grid on;title('显示某一次的仿真结果');%显示整体的平均效果
%显示整体的平均效果
%首先计算平均值
for i = 1:size(Package_Infor,1)for j = 1:size(Package_Infor,2)for m = 1:SIMU_NUMtmps1(i,j,m) = Package_Infor_Montecarlo{m}(i,j); endend
end
Package_Infor_Montecarlo_avg = zeros(size(Package_Infor,1),size(Package_Infor,2));
for j = 1:size(Package_Infor,2)Package_Infor_Montecarlo_avg(1,j) = mean(tmps1(1,j,:));Package_Infor_Montecarlo_avg(2,j) = mean(tmps1(2,j,:));Package_Infor_Montecarlo_avg(3,j) = mean(tmps1(3,j,:));Package_Infor_Montecarlo_avg(4,j) = mean(tmps1(4,j,:));Package_Infor_Montecarlo_avg(5,j) = mean(tmps1(5,j,:));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i = 1:length(Package_Index)for m = 1:SIMU_NUMtmps2(i,m) = Package_Index_Montecarlo{m}(i); end
end
for i = 1:length(Package_Index)Package_Index_Montecarlo_avg(i) = mean(tmps2(i,:));
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i = 1:length(FIFO_DATA)for m = 1:SIMU_NUMtmps3(i,m) = FIFO_DATA_Montecarlo{m}(i); end
end
for i = 1:length(FIFO_DATA)FIFO_DATA_Montecarlo_avg(i) = mean(tmps3(i,:));
endfigure
subplot(121);
plot([0 Package_Infor_Montecarlo_avg(1,Package_Index_Montecarlo_avg)],0:Num_FIFO_Package);
hold on;
plot([0 Package_Infor_Montecarlo_avg(4,Package_Index_Montecarlo_avg)],0:Num_FIFO_Package,'r-.');
hold off;
xlabel('The time');
ylabel('The Package');
legend('到达时间','离开时间');
grid on;
axis square;
title('显示整体的平均效果');subplot(122);
plot([0 Package_Infor_Montecarlo_avg(1,Package_Index_Montecarlo_avg)],0:Num_FIFO_Package);
hold on;
plot([0 Package_Infor_Montecarlo_avg(4,Package_Index_Montecarlo_avg)],0:Num_FIFO_Package,'r-.');
hold off;
axis([40,45,3500,4000]);
xlabel('The time');
ylabel('The Package');
legend('到达时间(局部显示效果)','离开时间(局部显示效果)');
grid on;
axis square;
title('显示整体的平均效果');figure;
subplot(121);
plot(1:Num_FIFO_Package,Package_Infor_Montecarlo_avg(3,Package_Index_Montecarlo_avg),'r-*');
hold on;
plot(1:Num_FIFO_Package,Package_Infor_Montecarlo_avg(2,Package_Index_Montecarlo_avg)+Package_Infor_Montecarlo_avg(3,Package_Index_Montecarlo_avg),'k-');
hold off;
legend('等待时间','处理所需要的时间');
grid on;
axis square;
title('显示整体的平均效果');subplot(122);
plot(1:Num_FIFO_Package,Package_Infor_Montecarlo_avg(3,Package_Index_Montecarlo_avg),'r-*');
hold on;
plot(1:Num_FIFO_Package,Package_Infor_Montecarlo_avg(2,Package_Index_Montecarlo_avg)+Package_Infor_Montecarlo_avg(3,Package_Index_Montecarlo_avg),'k-');
hold off;
axis([4000,4200,0,1.2*max(Package_Infor_Montecarlo_avg(3,4000:4200))]);
legend('等待时间(局部显示效果)','处理所需要的时间(局部显示效果)');
grid on;
axis square;
title('显示整体的平均效果');%绘制每一个时刻下,FIFO中的数据包的数量q(t)的函数变化
figure;
subplot(211);
bar(FIFO_DATA_Montecarlo_avg);
grid on;
legend('Q(t)整体显示效果');
axis([1,10000,0,1.2*max(FIFO_DATA_Montecarlo_avg)]);
title('显示整体的平均效果');
subplot(212);
bar(FIFO_DATA_Montecarlo_avg);
grid on;
legend('Q(t)局部显示效果');
axis([4000,4050,0,1.2*max(FIFO_DATA_Montecarlo_avg(4000:4050))]);
title('显示整体的平均效果');%比较最开始每个包之间的时间,和经过buffer还有traffic影响之后到达的每个包之间的时间差。
figure
plot(0:Num_FIFO_Package,[0 abs(Package_Infor_Montecarlo_avg(1,Package_Index_Montecarlo_avg)-Package_Infor_Montecarlo_avg(4,Package_Index_Montecarlo_avg))]);
ylabel('The time');
xlabel('The Package');
legend('时间差');
grid on;title('显示某一次的仿真结果');
30_001m4.本算法原理
服务级别协议(Service Level Agreement, SLA)是云服务提供商与其客户之间达成的一种正式协议,定义了服务质量的各种指标,如可用性、性能、支持等。其中,响应时间是指从用户发起请求到收到响应的时间间隔,它是衡量用户体验和系统性能的关键指标之一。在云计算环境中,确保快速且一致的响应时间对于维持高质量的服务至关重要。
响应时间受多种因素影响,包括但不限于:
网络延迟:数据在网络中传输所需的时间。
处理时间:服务器处理请求所需的时间。
队列等待时间:如果存在多个并发请求,新请求可能需要排队等待。
资源利用率:CPU、内存等硬件资源的使用情况直接影响处理速度。
软件效率:应用程序的设计和实现也会影响其执行效率。
为了更准确地理解和预测响应时间,可以采用一些数学模型来进行分析。这里介绍两种常用的模型:M/M/1排队模型和Little's Law。
M/M/1排队模型是一种经典的排队论模型,适用于描述具有单个服务台且到达和服务过程均服从泊松分布的情况。假设以下参数:

Little's Law 是排队论中的一个基本定理,它提供了一个简单但强大的工具来关联三个关键变量:L(系统中的平均请求数量)、λ(到达率)以及 W(每个请求在系统中的平均停留时间)。其表达式为:

综上所述,云计算SLA中的响应时间是一个涉及众多因素的综合性问题。通过对相关数学模型的研究与应用,不仅可以帮助我们深入理解系统行为,还能指导实践操作以达到最优效果。随着技术进步及市场需求变化,未来还将有更多创新方法被提出以进一步提升云计算服务质量。
5.完整程序
VVV
相关文章:

云计算SLA响应时间的matlab模拟与仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 5.完整程序 1.程序功能描述 用matlab模拟,一个排队理论。输入一堆包,经过buffer(一个或者几个都行)传给server,这些包会在buffer里…...
ARTS Week 42
Algorithm 本周的算法题为 2283. 判断一个数的数字计数是否等于数位的值 给你一个下标从 0 开始长度为 n 的字符串 num ,它只包含数字。 如果对于 每个 0 < i < n 的下标 i ,都满足数位 i 在 num 中出现了 num[i]次,那么请你返回 true …...

10.2学习
1.IOC控制反转 IoC(Inverse of Control:控制反转)是⼀种设计思想,就是将原本在程序中⼿动创建对象的控制权,交由Spring框架来管理。 IoC 在其他语⾔中也有应⽤,并⾮ Spring 特有。 IoC 容器是 Spring⽤来实现 IoC …...

【数一线性代数】021入门
Index 推荐阅读:https://blog.csdn.net/weixin_60702024/article/details/141729949分析实现总结 推荐阅读:https://blog.csdn.net/weixin_60702024/article/details/141729949 给定二叉树的根节点root,计算其叶节点的个数。 分析实现 类似…...
kubernetes中ConfigMap和Secret)
(k8s)kubernetes中ConfigMap和Secret
转载:ConfigMap 一、ConfigMap介绍 ConfigMap是一种API对象,用来将非机密性的数据保存到键值对中。使用时,Pod可以将其用作环境变量、命令行参数或存储卷中的配置文件。 ConfigMap将你的环境配置信息和容器镜像解耦,便于应用配置…...

stm32四足机器人(标准库)
项目技术要求 PWM波形的学习 参考文章stm32 TIM输出比较(PWM驱动LED呼吸灯&&PWM驱动舵机&&PWM驱动直流电机)_ttl pwm 驱动激光头区别-CSDN博客 舵机的学习 参考文章 stm32 TIM输出比较(PWM驱动LED呼吸灯&&PWM驱动舵机&&PWM驱动直流电机)…...

基于Hive和Hadoop的共享单车分析系统
本项目是一个基于大数据技术的共享单车分析系统,旨在为用户提供全面的单车使用信息和深入的出行行为分析。系统采用 Hadoop 平台进行大规模数据存储和处理,利用 MapReduce 进行数据分析和处理,通过 Sqoop 实现数据的导入导出,以 S…...

基于SSM和vue的机票订购管理系统
👉文末查看项目功能视频演示获取源码sql脚本视频导入教程视频 1 、功能描述 基于SSM和vue的机票订购管理系统2拥有两种角色 管理员:用户管理、机票管理、订票管理、公告管理、广告管理、系统管理、添加机票等 用户:登录注册、订票、查看公…...

【rCore OS 开源操作系统】Rust 练习题题解: Enums
【rCore OS 开源操作系统】Rust 练习题题解: Enums 摘要 rCore OS 开源操作系统训练营学习中的代码练习部分。 在此记录下自己学习过程中的产物,以便于日后更有“收获感”。 后续还会继续完成其他章节的练习题题解。 正文 enums1 题目 // enums1.rs // // No hi…...

VPN简述
文章目录 VPNVPN基础VPN类型 VPN VPN隧道安全 VPN基础 背景: 在网络传输中,绝大部分数据内容都是明文传输,存在很多安全隐患(窃听、篡改、冒充) 总部、分公司、办事处、出差人员、合作单位等需要访问总部网络资源 Vi…...
)
【Kubernetes】常见面试题汇总(四十九)
目录 110.假设一家公司希望通过采用新技术来优化其工作负载的分配。公司如何有效地实现这种资源分配? 111.考虑一家拼车公司希望通过同时扩展其平台来增加服务器数量。您认为公司将如何处理服务器及其安装? 特别说明: 题目 1-68 属于【…...

常见排序算法以及冒泡排序的基础使用方法
众所周知,冒泡排序是编程中最经典也是最简单的一种排序方法,它是通过重复访问对两个相邻的值进行比较,由于在互换的过程中,最大 (或最小) 的那个值会慢慢的交换到顶部,像汽水一样,故名“冒泡排序”。 let a…...
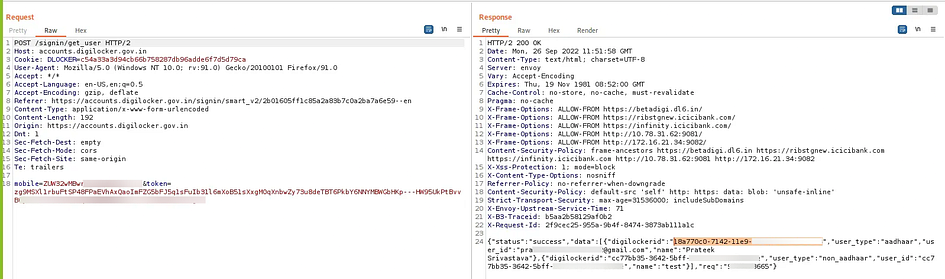
【网络安全】Cookie与ID未强绑定导致账户接管
未经许可,不得转载。 文章目录 前言正文前言 DigiLocker 是一项在线服务,旨在为公民提供一个安全的数字平台,用于存储和访问重要的文档,如 Aadhaar 卡、PAN 卡和成绩单等。DigiLocker 通过多因素身份验证(MFA)来保护用户账户安全,通常包括 6 位数的安全 PIN 和一次性密…...

Ansible Playbook原理与实践(Principles and Practice of Ansible Playbook)
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 本人主要分享计算机核心技…...

解决OpenCV保存视频 视频全部为绿色的bug
目录 项目场景: 问题描述 原因分析: 解决方案: 项目场景: 使用OpenCV-Python 保存视频,视频为numpy array格式,保存的视频全部为无意义的绿色。 问题描述 用opencv 保存的视频会出现全部为绿色的情况&…...

手机使用指南:如何在没有备份的情况下从 Android 设备恢复已删除的联系人
在本指南中,您将了解如何从 Android 手机内存中恢复已删除的联系人。Android 诞生、见证并征服了 80% 的智能手机行业。有些人可能将此称为“非常大胆的宣言”,但最近的统计数据完全支持我们的说法。灵活性、高度改进的可用性和快速性是 Android 操作系统…...
:函数)
TS系列(6):函数
你好,我是沐爸,欢迎点赞、收藏、评论和关注。 TS系列(1):TS是什么?如何使用? TS系列(2):类型声明、类型推断和类型总览 TS系列(3)&…...

网盘能否作为FTP替代产品?企业该如何进行FTP国产化替代?
近年来,信创的概念引入和高效实践落地让更多的行业企业自发性地进行国产化替代,目前信创国产化替代还多发生在操作系统和应用层面,软件工具等目前还在下一阶段规划,但很多企业未雨绸缪,已经在做调研和尝试。 FTP作为世…...

Python操作MongoDB
一、Python链接MongoDB 1、安装pymongo包 使用包管理器安装 pip3 insatll pymongo 2、连接MongoDB 首先需要导入pymongo包: from pymongo import MongoClient 创建MongoClient对象: from pymongo import MongoClient #创建MongoClient对象&#…...

Redis --- 第二讲 --- 特性和安装
一、背景知识 Redis特性: Redis是一个在内存中存储数据的中间件,用于作为数据库,作为缓存,在分布式系统中能够大展拳脚。Redis的一些特性造就了现在的Redis。 在内存中存储数据,通过一系列的数据结构。MySQL主要是通…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
