数学建模--什么是数学建模?数学建模应该怎么准备?
前言
- 这是去年底学数学建模老哥的建模课程笔记;
- 未来本人将陆陆续续的更新数学建模相关的一些基础算法,大家可以持续关注一下;
- 提示:数学建模只有实战才能提升,光学算法没有啥意义,也很难学的很懂。
文章目录
- 如何分模块学习?
- 数学建模流程
- 阅读论文的流程
- 问题分类
- 评价类
- 预测类
- 优化类
如何分模块学习?
- 题目备战:掌握固定模式
- 基于模型的研究和分析
- 摘要备战:总结归纳能力,通过看高水平论文和优秀论文
- 问题分析:动脑能力是关键,第一步进行问题定性,然后说明如何求解这类问题
- 模型的建立:将常见的模型进行归纳总结,形成算法库
- 模型优缺点:对模型不足需要提前掌握,并且阐述不足
数学建模流程

- 模型准备
- 了解问题的实际背景,明确其意义,掌握对象的各种信息
- 数据,变量/参数
- 了解问题的实际背景,明确其意义,掌握对象的各种信息
- 模型假设
- 根据实际对象的特征和建模的目的,对问题进行必要简化,最重要的点之一,评委最喜欢看中点之一
- 如预测未来十年中国人口变化, 可假设未来十年疾病、灾害对人口变化影响不大
- 根据实际对象的特征和建模的目的,对问题进行必要简化,最重要的点之一,评委最喜欢看中点之一
- 模型建立
- 在假设基础上,利用适当的数学工具来规划各个变量之间的关系,两大王牌:流程图,伪代码
- 流程图:一般建立组合模型(单个模型效果不好),如:灰色预测-BP神经网络
- 伪代码:包含输入,输出。过程
- 模型求解
- 利用获取的数据资料,对模型的所有参数做出计算
- 一般流程为:基于……数据,经行……预处理工作,得到……参数,进而得到……结果,结果如下:
- 模型分析
- 对所建的模型的思路进行阐述,对所得结果进行数学分析
- 一定要和问题相呼应
- 一定要有表层分析和深层分析
- 表层分析:看图说话
- 深层分析:看图挖掘得出的
- 模型检验
- 检验模型的准确性和合理性等,如:灵敏度分析(美赛最爱),误差分析
阅读论文的流程
比方说,2012年A题葡萄酒评价模型,有篇文章用了回归分析和灰色关联方法对葡 萄酒进行了评级,然后比较二者的结果,得出灰色关联的方法更加能够反映理化成 分对葡萄酒质量的影响的结论。这就是论文表面上给我们呈现的样子,但是我们就 可以多想想以下几个问题:
(1) 葡萄酒的理化成分数据是怎么一个结构?作者用了哪些数据处理方法,缺失、 异常数据怎么处理的?他为什么要这么处理?如果以后遇到类似的问题,数据分析 的时候,有没有好的步骤?
简要来说,这道题的理化指标是一个多变量多对象的二维数据表,存在异常数据用 spss验证数据功能予以去除,缺失值用插值方法补充,然后用主成分分析法进行了 降维,目的是能够减小变量个数。这样一来,数据分析的一套流程就比较清楚了。
(2) 他为什么选取了回归分析和灰色关联方法来建模?遇到这类评 价某事物的问题,一共有哪些建模方法?分别能够在什么条件下使用? 各有什么特点?
回归分析能够忽略问题机理,只从数据上分析出变量之间的相关关系, 进而得出结论;而灰色关联方法能够在机理没有完全摸清的情况下, 部分挖掘变量间更深层次的联系,更能够准确地评价葡萄酒的好坏。 在评价类问题上,我们还有TOPSIS方法,模糊综合评判等等,各有各 的特点和优势,处理的问题类型有较小的差别,大家可以自行学习。
(3)在做模型检验时,他是用什么标准来得到判断灰色关联方法比回归 分析要好的结论的?他怎么想法到这点的?遇到这种比较时能不能够想到 这一点上?
该文章直接用了评价误差率指标来判别评价好坏,并且从模型的假设、简 化等建立过程中分析出灰色关联方法更加优越的结论,于是我们在对两个模型进行优劣比较的时候,也应该从结果和建立过程分析,进而比较优劣。 从这个思路中间大家应该基本能知道,下次再遇到西瓜酒,葡萄汁,或者 电脑的评价问题数据应该怎样进行处理了,我们要类比的是数学结构,而 不是表面上这个东西是葡萄酒还是白酒,这篇论文读透了,以此为线索, 整个评价问题你都解决了。
问题分类

评价类

- 选择合适指标
- 系统分析法:选择什么指标(选择主要影响的)
- 同向化处理:数据要么同降,要么同时升
- 指标无量化处理:数据大小统一,去除单位影响
- 权重各指标:详情看算法匹配大全

- 模糊评价:可以看有无"问卷调查"
预测类
预测就是根据过去和现在估计未来,预测未来。统计预测属于预测方法研究范畴,即如何利用科学的统计方法对物的未来发展进行定量推测

- 搜索和审核治疗:找数据
- 误差分析必须要有,预测类最核心的
- 算法详情:算法匹配表

优化类
优化类问题是从所有可能方案中选择最合理的方案以达到最优目标。在各种科学问题、工程问题、生产管理、社会经济问题中,人们总是希望在有限的资源条件下,用尽可能小的代价,获得最大的收获(比如保险)。
● 优化类问题一般的解题步骤(3步)为:
● (1)首先确定决策变量,也就是需要优化的变量;
● (2)然后确定目标函数,也就是优化的目的;
● (3)最后确定约束条件,决策变量在达到最优状态时, 受到那些客观限制

- 决策变量:对结果有直接影响的
- 0-1规划:结果只有两个
算法的选择,详情看算法匹配大全
优化类问题中常用的数学模型和求解算法,其中包括线性规划、非线性规划、整数规划、多目标规划等。在模型求解中,对于凸优化模型,可以采用基于梯度的求解算法;对于非凸的优化模型,可以采用智能优化算法。

相关文章:

数学建模--什么是数学建模?数学建模应该怎么准备?
前言 这是去年底学数学建模老哥的建模课程笔记;未来本人将陆陆续续的更新数学建模相关的一些基础算法,大家可以持续关注一下;提示:数学建模只有实战才能提升,光学算法没有啥意义,也很难学的很懂。 文章目录…...

Java项目实战II基于Java+Spring Boot+MySQL的智能物流管理系统(源码+数据库+文档)
目录 一、前言 二、技术介绍 三、系统实现 四、文档参考 五、核心代码 六、源码获取 全栈码农以及毕业设计实战开发,CSDN平台Java领域新星创作者 一、前言 随着电商行业的蓬勃发展,物流行业迎来了前所未有的机遇与挑战。面对日益增长的订单量和复…...
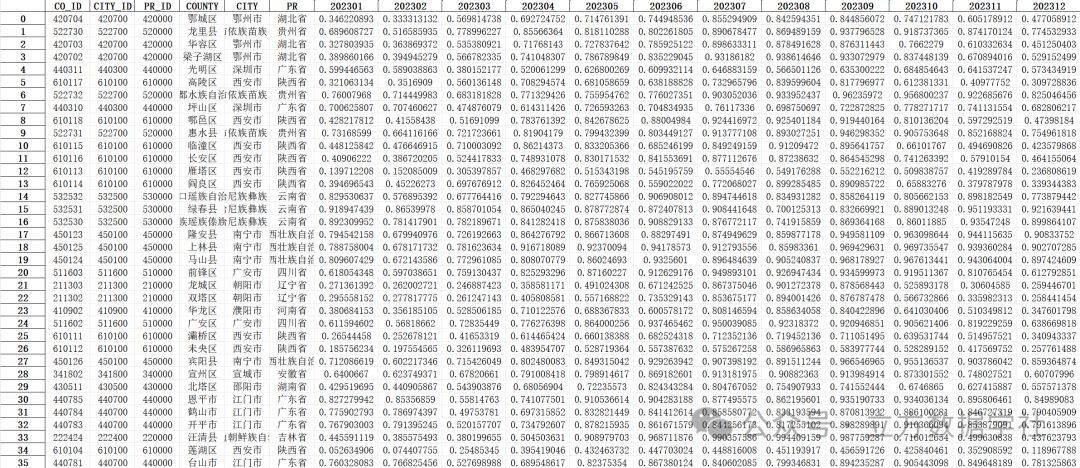
【数据分享】2000—2023年我国省市县三级逐月植被覆盖度(FVC)数值(Shp/Excel格式)
之前我们分享过2000—2023年我国250米分辨率逐月植被覆盖度(FVC)栅格数据(可查看之前的文章获悉详情),该数据来源于高吉喜等学者在国家青藏高原科学数据中心平台上分享的数据,合成方式采用月最大值合成&…...

《Linux从小白到高手》理论篇(十一):Linux的系统环境管理
值此国庆佳节,深宅家中,闲来无事,就多写几篇博文。本篇详细深入介绍Linux的系统环境管理。 环境变量 linux系统下,如果你下载并安装了应用程序,很有可能在键入它的名称时出现“command not found”的提示内容。如果每…...

Qt/C++开源控件 自定义雷达控件
使用Qt框架创建一个简单的雷达图,包含动态扫描、目标点生成、刻度和方向标识。代码实现使用C编写,适合用作学习和扩展的基础。 1. 头文件与基本设置 #include "RadarWidget.h" #include <QPainter> #include <QPen> #include &…...
?)
什么是IDE(集成开发环境)?
集成开发环境(IDE)详解 在软件开发的世界中,集成开发环境(IDE,Integrated Development Environment)扮演着至关重要的角色。它是一个综合性的软件应用程序,旨在为软件开发者提供一整套的、易于使用的工具集,以便他们能够更高效地编写、调试、测试和部署代码。简而言之…...

【Linux】用虚拟机配置Ubuntu 24.04.1 LTS环境
目录 1.虚拟机安装Ubuntu系统 2.Ubuntu系统的网络配置 3.特别声明 首先我们先要下载VMware软件,大家自己去下啊! 1.虚拟机安装Ubuntu系统 我们进去之后点击创建新的虚拟机,然后选择自定义 接着点下一步 再点下一步 进入这个界面之后&…...

MacOS升级Ruby版本详解:步骤、挑战与解决方案
MacOS升级Ruby版本详解:步骤、挑战与解决方案 在MacOS上升级Ruby版本是一个涉及多个步骤和考虑因素的过程。Ruby作为一种广泛使用的编程语言,其新版本通常会引入一系列改进,包括性能优化、安全修复和新特性。因此,升级Ruby版本不…...

Log4j的配置与使用详解
Log4j的配置与使用详解 Log4j介绍 Log4j是Apache的一个开源项目,通过使用Log4j,我们可以控制日志信息输送的目的地是控制台、文件、GUI组件,我们可以控制每条日志的输出格式;只需要通过一个配置文件就可以灵活的配置,…...

docker 的目录有那些,分别存放什么东西
Docker 的目录结构和文件存放位置取决于你所使用的操作系统和Docker的版本。以下是一些常见的目录和它们通常存放的内容: 通用目录 /var/lib/docker (Linux) 这是Docker在Linux系统上的主要数据目录。存放了镜像、容器、数据卷、网络等的元数据和状态信息。具体结构…...
)
开源模型应用落地-模型微调-语料采集-数据格式化(四)
一、前言 在自然语言处理(NLP)的快速发展中,语料采集作为基础性的步骤显得尤为重要。它不仅为机器学习模型提供了所需的训练数据,还直接影响模型的性能和泛化能力。随着数据驱动技术的不断进步,如何有效并高效地收集、清洗和整理丰富多样的语料,已成为研究者和工程师们亟…...

C语言+单片机
今天内容有点水哈哈(忙着练焊铁技术了嘻嘻) C语言 简单学习了while语言以及其与for语言的区别和适用方法 .循环结构: 初始化语句条件判断句条件控制句 for语句 for(int1;i<100;i){执行条件} for (int i 1; i < 100; i) {printf(&quo…...

vmvare虚拟机centos 忘记超级管理员密码怎么办?
vmvare虚拟机centos 忘记超级管理员密码怎么办?如何重置密码呢? 一、前置操作 重启vmvare虚拟机的过程中,长按住Shift键 选择第一个的时候,按下按键 e 进入编辑状态。 然后就会进入到类似这个界面中。 在下方界面 添加 init=/bin/sh,然后按下Ctrl+x进行保存退出。 init=/bi…...

使用 Vue3 和 Axios 实现 CRUD 操作
文章目录 1、准备工作2、创建 Vue 3 项目3、项目结构4、实现 CRUD 操作5、运行项目6、小结在当今的前端开发中,Vue.js 作为一款流行的 JavaScript 框架,正在被越来越多的开发者所青睐。尤其是 Vue 3 引入了 Composition API 和更优雅的响应式处理,使得模板编写和状态管理变得…...
下拉选框控件)
.NET MAUI(.NET Multi-platform App UI)下拉选框控件
MAUI下拉选框控件详解: 在开发跨平台应用程序时,下拉选框(ComboBox)是一个极为常见且实用的控件,它允许用户从一组预定义的选项中选择一个。在.NET MAUI(.NET Multi-platform App UI)框架中&am…...

C++平台跳跃游戏
目录 开头程序Game.cpp源文件Player.h头文件Player.cpp源文件 程序的流程图程序游玩的效果下一篇博客要说的东西 开头 大家好,我叫这是我58。 程序 Game.cpp源文件 #include <iostream> #include "Player.h" using namespace std; void printma…...

多系统萎缩患者必看!这些维生素助你对抗病魔
亲爱的朋友们,今天我们来聊聊一个相对陌生但重要的健康话题——多系统萎缩(MSA)。这是一种罕见的神经系统疾病,影响着患者的自主神经系统、运动系统和平衡功能。面对这样的挑战,科学合理的饮食和营养补充显得尤为重要。…...

深度学习模型性能优化实战之从评估到提升的全流程解析
1. 概述 在构建和使用机器学习模型的过程中,模型的效果评估和优化是两个至关重要的环节。无论模型是用于分类、回归还是其他任务,评估其表现以及持续优化模型性能,都是确保模型在实际应用中取得成功的关键。本节将重点介绍模型效果评估的定义…...

C++ | Leetcode C++题解之第446题等差数列划分II-子序列
题目: 题解: class Solution { public:int numberOfArithmeticSlices(vector<int> &nums) {int ans 0;int n nums.size();vector<unordered_map<long long, int>> f(n);for (int i 0; i < n; i) {for (int j 0; j < i;…...
)
【解密 Kotlin 扩展函数】扩展属性与扩展函数类似(十九)
导读大纲 1.1.1 扩展属性的创建和使用 1.1.1 扩展属性的创建和使用 之前, 我们已经了解声明 Kotlin 属性的语法 Kotlin中的顶级属性–传送门就像扩展函数一样,我们也可以指定扩展属性就像之前所说,属性和函数的区别在于前者是特征,后者是行为 相比扩展函…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
