阿里云 SAE Web:百毫秒高弹性的实时事件中心的架构和挑战
作者:胡志广(独鳌)
背景
Serverless 应用引擎 SAE 事件中心主要面向早期的 SAE 控制台只有针对于应用维度的事件,这个事件是 K8s 原生的事件,其实绝大多数的用户并不会关心,同时也可能看不懂。而事件中心,是希望能够成为一个更高维度入口,可以总览全局的事件(着重于异常事件),并且配置相关的通知与告警。
建设事件中心和监控最大的区别在于:
- 监控: 监控主要在关注异常指标的监控告警和可观测能力上。
- 事件中心: 主要是系统进行诊断抽象后面向用户更紧急和具体定位的事件可以让用户进行一键订阅和提前告警,面向智能运维的方向进行建设。
事件中心的核心意义在于通过显示、通知来将 SAE 上的应用与用户更紧密的连接起来。
事件中心整体能力大图如下:
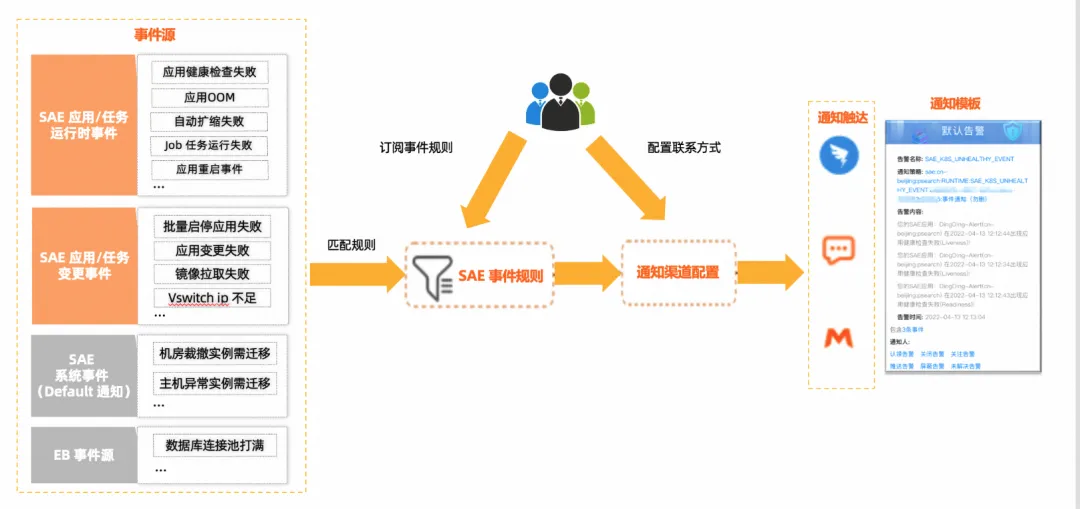
SAE Web 上线后对于用户的事件需求更加的敏感,因为 Web 支持百毫秒弹性,所以对于事件的实时性和可靠性的要求更高,对于用户的通知和告警消息感知也更重要,针对这些需求 SAE 针对 Web 进行开发了事件中心让用户可以更好的感知异常事件。
整体架构
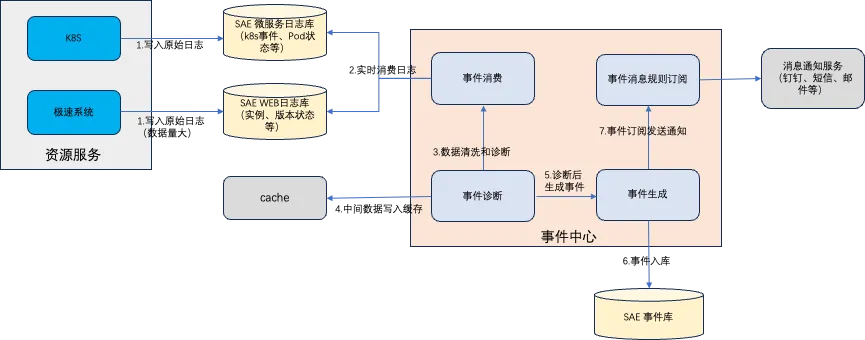
-
资源服务
- K8s:针对 K8s 的原始事件等各种记录入库,包括 pod、workload、网络等。
- 极速系统:主要是针对 Web 的场景开发的百毫秒资源服务,实时性和弹性高,这里主要将实例信息、版本切换事件原始信息入库。
-
事件中心
- 事件消费:主要实时消费日志库中的原始数据进行监听。
- 事件诊断:原始数据量过大冗余信息也多,所以需要事件诊断进行数据清洗和把中间数据写入 cache 临时保存。
- 事件生成:数据诊断完成后,根据固定的事件模型写入到事件库保存。
- 事件消息规则订阅:根据用户订阅的规则将生成好的事件通过消息通知服务进行告警通知,包括:钉钉、短信、邮件等。
技术挑战
技术选型
-
全新实现一套 SAE Web 事件架构
- 优点:历史包袱小,实现更优雅。
- 缺点:研发周期长和之前的前后端需要兼容。
-
基于 SAE 微服务事件架构实现
- 优点:事件模型是现成的,实现简单和现有系统兼容。
- 缺点:无法处理 Web 的海量数据,存在数据瓶颈。
-
最终方案: 事件模型采用 SAE 微服务事件中心架构实现写入,但是 Web 的事件不直接写入事件而是通过一层数据清洗后写入事件库避免信息爆炸。
数据爆炸
资源数据架构现状
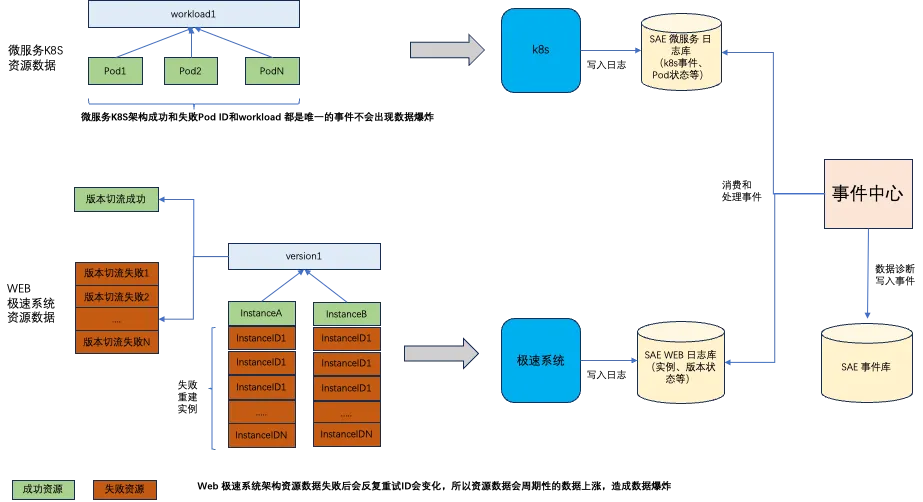
微服务 K8s 资源架构
微服务 K8s 资源架构基于 K8s 基础之上建设的,所以对于 workload 和 pod 当资源异常状态的时候会重试非重建,所以 workload 的 key 和 pod 的 key 是唯一的,这时是不会造成事件信息的数据爆炸的,所以最终通过组件将原始事件信息写入到日志库中最终通过事件中心进行消费。
Web 极速系统资源架构
Web 是自主研发的一套极速系统可以实现百毫秒弹性实例的资源系统,可以通过流量控制弹性,闲置时进行缩容。
-
实例资源: 实例主要通过预留和弹性扩容的方式进行创建,一般通过流量控制弹性扩容,没有流量访问时则动态缩容。
- 实例弹性扩容/缩容成功:扩容和资源闲置时进行缩容,除了预留资源是固定的 ID,其他的资源可能随时弹出和缩容,这里和微服务 K8s 架构固定实例的模式有很大差异,所以资源实例数据也会多很多。
- 实例弹性扩容失败:当实例出现异常的时候(包括镜像拉取失败、健康检查失败、其他创建失败等原因),那么将会不断的进行重试,所以实例的 ID 也会变化,这时将会有很多的失败实例信息。
-
版本切流: 微服务 K8s 架构是根据 workload 进行部署发布,Web 是基于版本流量进行发布。
- 版本切流成功:版本切流成功就是产生一条事件,这里主要会根据版本比例产生一些事件信息。
- 版本切流失败:版本切流失败因为和实例弹性有关系,所以也受弹性实例失败影响,当弹性失败的时候版本切流同样也是失败会进行重试,并且版本切流还会存在部分成功和部分失败的场景,这种当面临同版本失败过多时也会存在信息爆炸的风险。
-
数据爆炸风险: 基于上述内容 Web 架构的实例会动态的扩容和缩容,失败的时候不断的重建实例造成 ID 会重建,包括版本失败的信息也和实例扩缩容有关系,所以资源的事件数据量要远远大于微服务 K8s 架构的事件数据。
解决方案
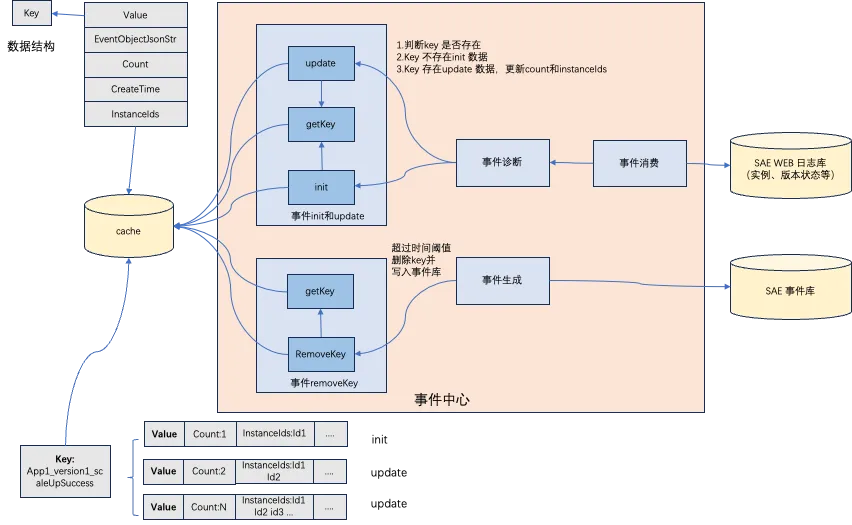
数据爆炸解决方案:通过分布式缓存进行数据聚合,根据时间阈值后进行事件生成,其实类似一种数据队列的模式。
- key:应用 ID+版本 ID+事件类型,如:app1_version1_scaleUpSuccess。
- 事件消费+初始化缓存:消费原始日志后判断事件 key 是否在缓存中,如果不在缓存中则调用 init 函数初始化 cache 数据,初始化 count:1 和 instanceId:1,如果失败的则不存在 InstanceId。
- 事件消费+更新缓存:消费原始日志后如果事件 key 在缓存中则将缓存数据进行更新 count 和 instanceId 进行聚合,如:count2,instanceIds:id1,id2 这样(之前只有 id1),以此类推。
- 事件生成:根据时间阈值定时出队,比如 60s 后,如果 key 内的 createtime 超过 60s 则调用 remove 方法删除缓存事件生成到标准的 sae 事件库中按照格式。
数据爆炸最初用的缓存方案,但是没有采用分布式锁,所以出现了事件中心管控多任务实例造成了同一个事件写入重复多份的问题,下面有问题和优化方案。
- 问题:最初只是在内存中保存,所以当多实例时每个实例都会写入到事件库就会存在数据冗余。
- 优化方案:队列采用分布式锁的方式处理,避免多实例重复写入事件的问题。
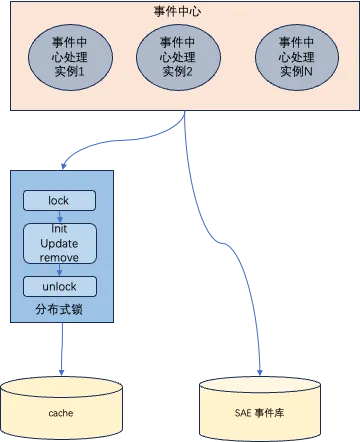
Full Gc
问题:因为基于微服务事件中心架构的模型是 java,最初是一次性获取缓存中所有的事件记录写到一个 Java 的 HashMap 中,而这一个 hashmap 有几百兆,如果在事件生成时比较慢会有多个线程都进行拉取就会造成上一个对象没回收下一个线程又获取了一个新的对象,这样就很容易 full gc 了,问题的监控图如下:
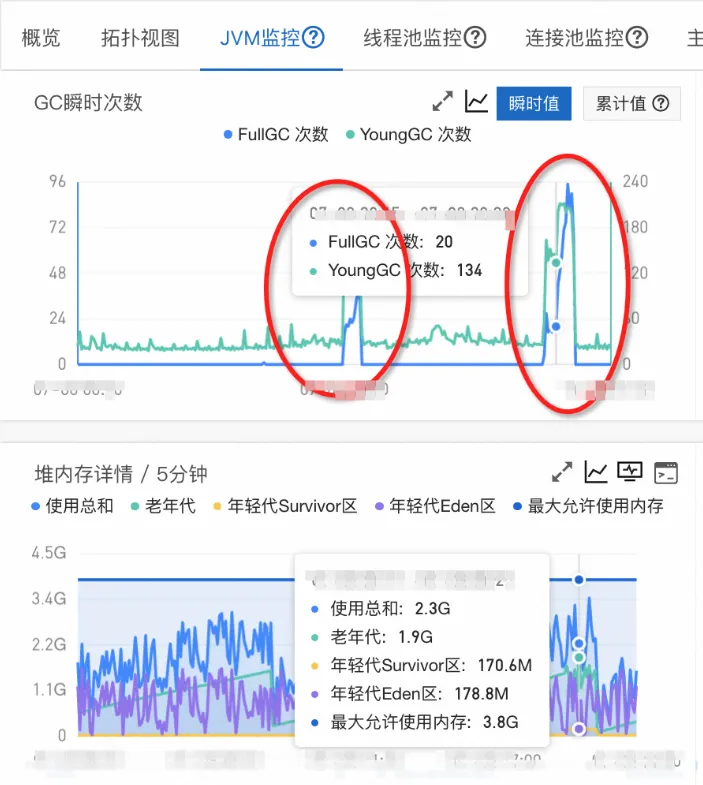
优化:
-
这个问题其实是有 2 个问题:
- 早期不是所有的事件类型都是类似队列的模式进行处理,就是入队和阈值出队的模式,所以某个事件异常后就会产生数据爆炸。
- 一次性拉取缓存所有的数据设置到 Java 的 hashmap,数据量过大如果处理慢则会造成变量一直在函数内没有释放容器造成内存泄露和触发 full gc。
-
优化内容:
- 优化一:所有的事件类型都采用入队和出队的模式进行处理,这样可以降低很多数据积压,到达阈值后都会进行事件写入和去重。
- 优化二:对于拉取缓存的数据进行分布式分片处理让整体的数据变小,比如 1/20 的数据量相对之前几百兆就缩小 20 倍,这样内存就直接下降了处理速度也快可以完美解决 full gc 问题。
- 优化后的效果图如下:
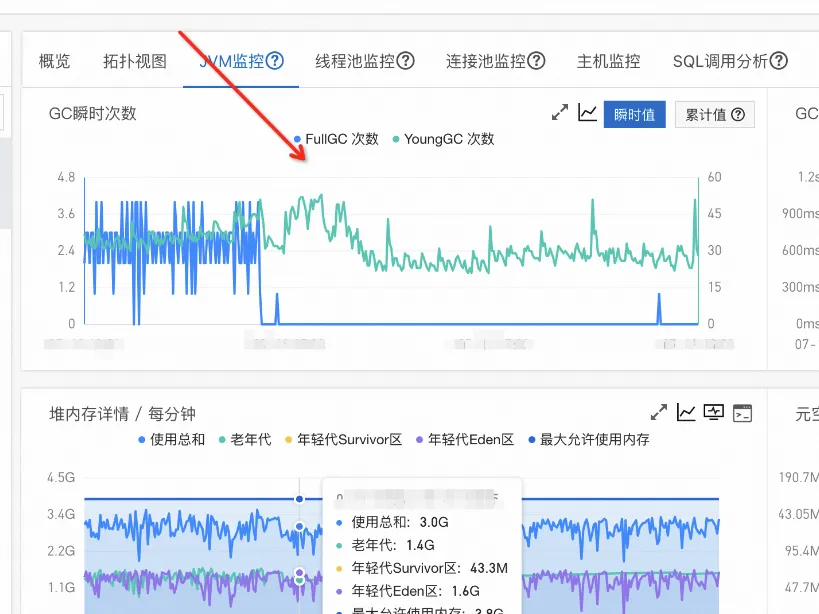
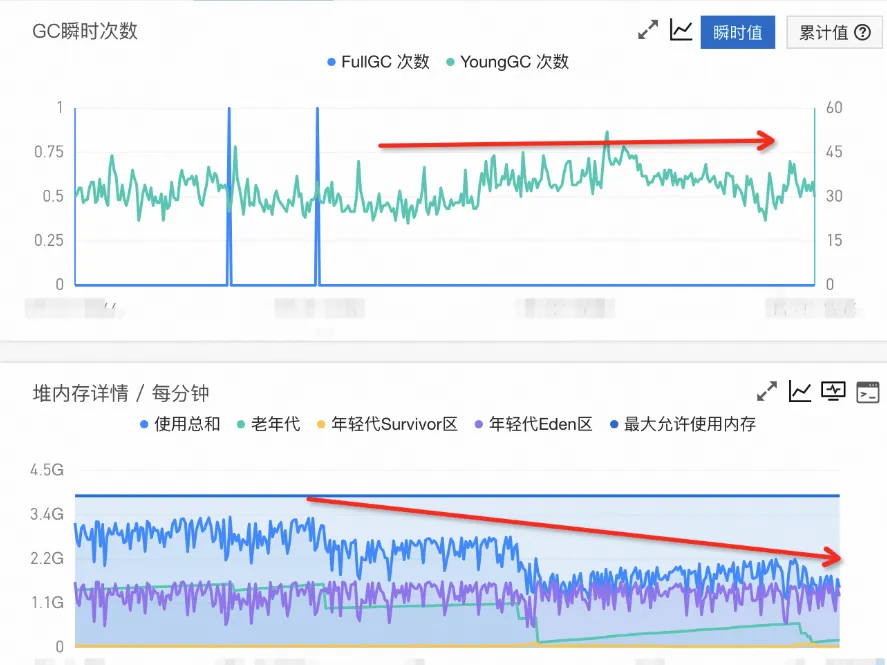
未来和展望
因为面向资源的原始事件相对于 SAE 的用户来讲太难理解了,所以事件中心的出现是更简单的帮助用户进行诊断和定位问题并且第一时间进行通知更加及时的定位问题根据事件,目前很多用户基于 SAE 的事件中心发现问题并诊断自闭环,比如南瓜电影、迅捷联动等用户。
事件中心不仅仅提供白屏化和可订阅通知能力,还可以和用户的运维系统进行定制化集成起来,如:南瓜电影将事件中心集成到了运维平台。
未来计划在事件中心上丰富更多的诊断和智能运维事件结合 AI 场景进行分析和定位让用户可以精确锁定问题和快速处理,实现真正一键定位和简单运维。
相关文章:

阿里云 SAE Web:百毫秒高弹性的实时事件中心的架构和挑战
作者:胡志广(独鳌) 背景 Serverless 应用引擎 SAE 事件中心主要面向早期的 SAE 控制台只有针对于应用维度的事件,这个事件是 K8s 原生的事件,其实绝大多数的用户并不会关心,同时也可能看不懂。而事件中心,是希望能够…...

人口普查管理系统基于VUE+SpringBoot+Spring+SpringMVC+MyBatis开发设计与实现
目录 1. 系统概述 2. 系统架构设计 3. 技术实现细节 3.1 前端实现 3.2 后端实现 3.3 数据库设计 4. 安全性设计 5. 效果展示 编辑编辑 6. 测试与部署 7. 示例代码 8. 结论与展望 一个基于 Vue Spring Boot Spring Spring MVC MyBatis 的人口普查管理…...
使用VBA快速将文本转换为Word表格
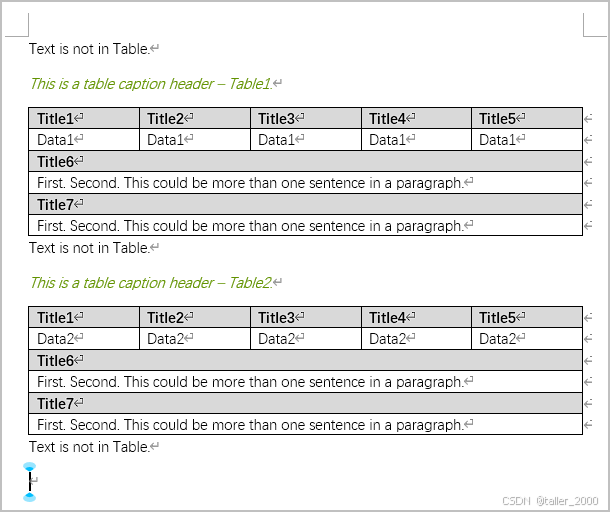
Word提供了一个强大的文本转表格的功能,结合VBA可以实现文本快速转换表格。 示例文档如下所示。 现在需要将上述文档内容转换为如下格式的表格,表格内容的起始标志为。 示例代码如下。 Sub SearchTab()Application.DefaultTableSeparator "*&quo…...

力扣题解1870
这道题是一个典型的算法题,涉及计算在限制的时间内列车速度的最小值。这是一个优化问题,通常需要使用二分查找来求解。 题目描述(中等) 准时到达的列车最小时速 给你一个浮点数 hour ,表示你到达办公室可用的总通勤时…...

D3.js数据可视化基础——基于Notepad++、IDEA前端开发
实验:D3.js数据可视化基础 1、实验名称 D3数据可视化基础 2、实验目的 熟悉D3数据可视化的使用方法。 3、实验原理 D3 的全称是(Data-Driven Documents),是一个被数据驱动的文档,其实就是一个 JavaScript 的函数库,使用它主要是用来做数据可视化的。本次实…...

在Robot Framework中Run Keyword If的用法
基本用法使用 ELSE使用 ELSE IF使用内置变量使用Python表达式本文永久更新地址: 在Robot Framework中,Run Keyword If 是一个条件执行的关键字,它允许根据某个条件来决定是否执行某个关键字。下面是 Run Keyword If 的基本用法: Run Keyword…...

虚拟机ip突然看不了了
打印大致如下: 解决办法 如果您发现虚拟机的IP地址与主机不在同一网段,可以采取的措施之一是调整网络设置。将虚拟机的网络模式更改为桥接模式,这样它就会获得与主机相同的IP地址,从而处于同一网段。或者,您可以使用…...

LeetCode[中等] 763. 划分字母区间
给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。 注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。 返回一个表示每个字符串片段的长度的列表。 思路 贪心…...

Java LeetCode每日一题
997. 找到小镇的法官 package JavaExercise20241002;public class JavaExercise {public static void main(String[] args) {int[][] array {{1,3},{2,3},{3,1}};Solution solution new Solution();System.out.println(solution.findJudge(3, array));} }class Solution {pu…...

数据结构--集合框架
目录 1. 什么是集合框架 2. 背后所涉及的数据结构以及算法 2.1 什么是数据结构 2.2 容器背后对应的数据结构 1. 什么是集合框架 Java 集合框架 Java Collection Framework ,又被称为容器 container ,是定义在 java.util 包下的一组接口 int…...

Win10鼠标总是频繁自动失去焦点-非常有效-重启之后立竿见影
针对Win10鼠标频繁自动失去焦点的问题,可以尝试以下解决方案: 一、修改注册表(最有效的方法-重启之后立竿见影) 打开注册表编辑器: 按下WindowsR组合键,打开运行窗口。在运行窗口中输入“regedit”&#x…...

智能涌现|迎接智能时代,算力产业重构未来
前言 OpenAI首席执行官山姆奥特曼在《智能时代》中描绘了一个令人振奋的未来图景,其中算力产业将扮演至关重要的角色。奥特曼预测,我们可能在“几千天内”迎来超级智能,这一进程将极大加速社会结构的智能化转型。 这一预测与算力产业的未来…...

关于HTML 案例_个人简历展示01
案例效果展示 代码 <!DOCTYPE html> <lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>个人简历信息</title> </he…...

【前端开发入门】css快速入门
目录 引言一、css盒模型1. 盒模型概念2. 盒模型案例 二、css编写1. html文件内部编写1.1 标签style属性编写1.2 css选择器关联1.2.1 id选择器1.2.2 class选择器1.2.3 标签选择器1.2.4 css选择器作用域1.2.5 其他选择器1.2.6 各css选择器优先级 2. 单独维护css文件2.1 创建css文…...

java中创建不可变集合
一.应用场景 二.创建不可变集合的书写格式(List,Set,Map) List集合 package com.njau.d9_immutable;import java.util.Iterator; import java.util.List;/*** 创建不可变集合:List.of()方法* "张三","李四","王五…...
D25【 python 接口自动化学习】- python 基础之判断与循环
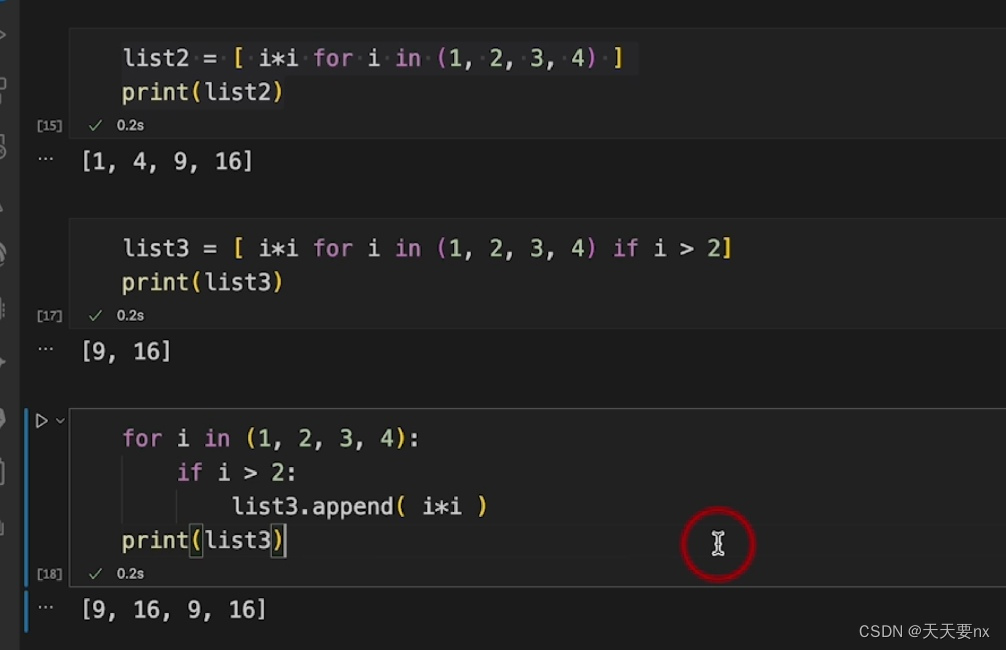
day25 for 循环 学习日期:20241002 学习目标:判断与循环﹣-35 for 循环:如何遍历一个对象里的所有元素? 学习笔记: for 循环与while循环的区别 for循环的定义 使用for循环遍历序列 使用for循环遍历字典…...

HTTP1.0和HTTP1.1有什么区别
HTTP/1.0 和 HTTP/1.1 是两个不同版本的 HTTP 协议。虽然它们的核心功能都是提供网页数据传输,但 HTTP/1.1 对 HTTP/1.0 做了很多改进,提升了性能和灵活性。以下是它们的主要区别: 1. 持久连接(Persistent Connection)…...

卡夫卡的理解
一、架构理解 在这个单聊新架构中,涉及多个服务器组件共同协作来实现单聊功能。 ChatAccessServer:可能负责处理单聊相关的访问请求,比如用户登录单聊以及发送单消息的请求接入。ChatHttpPushServer:推测其用于通过 HTTP 协议推…...

基础算法之滑动窗口--Java实现(上)--LeetCode题解:长度最小的子数组-无重复字符的子串-最大连续1的个数III-将x减到0的最小操作数
这里是Thembefue 今天讲解算法中较为经典的一个算法 > 滑动窗口 本讲解主要通过题目来讲解以理解算法 讲解分为三部分:题目解析 > 算法讲解 > 编写代码 滑动窗口 在正式进入题目的讲解之前,得先了解一下什么是滑动窗口,以及应该在什…...

Linux -- 文件系统(文件在磁盘中的存储)
目录 前言: 了解机械磁盘 初始盘片与磁头 盘片是怎么存数据的呢? 详解盘片 如何访问磁盘中的一个扇区呢? -- CHS 定位法 磁盘的逻辑存储 LBA(Logical Block Addressing --- 逻辑块寻址) 如何将 LBA 地址转换为…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
