前缀和算法详解

对于查询区间和的问题，可以预处理出来一个前缀和数组 dp，数组中存储的是从下标 0 的位置到当前位置的区间和，这样只需要通过前缀和数组就可以快速的求出指定区间的和了，例如求 l ~ r 区间的和，就可以之间使用 dp[l - 1] - dp[r] 来计算

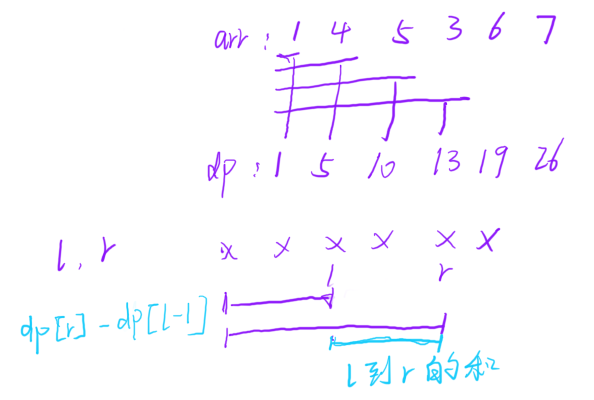
1. DP34 【模板】前缀和

DP34 【模板】前缀和

这里从下标 1 开始填是为了在初始化前缀和数组时更方便

public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int N = sc.nextInt();int p = sc.nextInt();int[] arr = new int[N + 1];long[] dp = new long[N + 1];for (int i = 1; i <= N; i++) {arr[i] = sc.nextInt();}for (int i = 1; i <= N; i++) {dp[i] = dp[i - 1] + arr[i];}int l = 0, r = 0;while (p-- != 0) {l = sc.nextInt();r = sc.nextInt();System.out.println(dp[r] - dp[l - 1]);}}
}

2. DP35 【模板】二维前缀和

二维前缀和模版

和一维的前缀和数组类似，这里需要先预处理出来一个前缀和矩阵 dp[][]，dp[i][j] 就表示从（1,1）到（i，j）这个矩阵中的所有元素的和

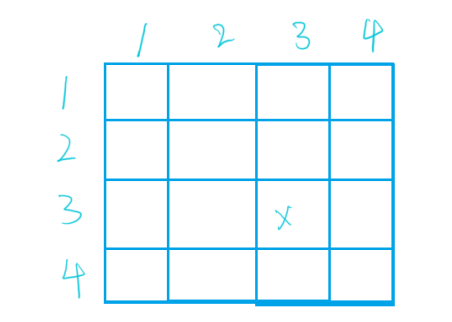
放到矩阵中可以看出，如果想要求（1,1）到（i，j）区间内的区域和，需要先加上 A，B，C，D 四个区域的和，如果单独的表示 B 区域或者 C 并不好表示，但是 A + B 和 A + C 是很好表示的，把这两个区域加起来再减去多加的 A ，再加上 D 就是整个区域的和

得到了前缀和数组之后，该怎么去使用呢？

如果说给出了（x1,y1）（x2,y2）两个点，那么就是求红色框的元素的和

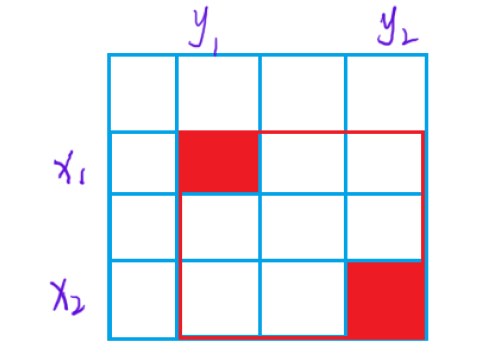
也就是求出 D 区域的和，由于 B 和 C 并不好单独转换，就可以转化为 A+B+C+D 的值先减去 A+B 的值，再减去 A + C 的值，此时方法 A 被多减了一次，再加上就是 D 区域的和了

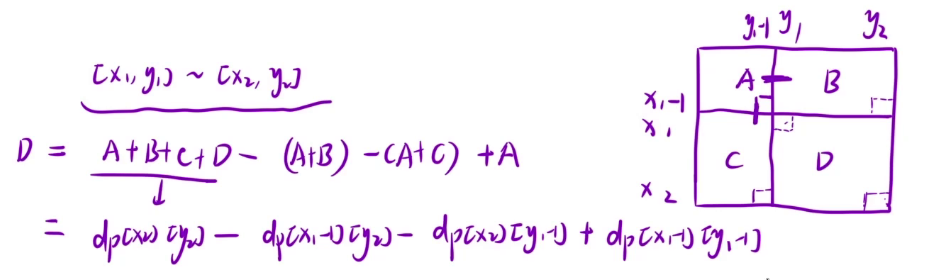
public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt(), m = sc.nextInt();int q = sc.nextInt();int[][] A = new int[n + 1][m + 1];long[][] dp = new long[n + 1][m + 1];for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {A[i][j] = sc.nextInt();}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {dp[i][j] = dp[i][j - 1] + dp[i - 1][j] - dp[i - 1][j - 1]+ A[i][j];}}int x1 = 0,y1 = 0,x2 = 0,y2 = 0;while (q-- != 0) {x1 = sc.nextInt();y1 = sc.nextInt();x2 = sc.nextInt();y2 = sc.nextInt();System.out.println(dp[x2][y2] - dp[x2][y1 - 1] - dp[x1 - 1][y2] + dp[x1 - 1][y1 - 1]);}}
}

3. 寻找数组的中心下标

724. 寻找数组的中心下标

根据题目要求就是求 0~ i - 1区间的和是否和区间 i + 1~n - 1 的和相等，那么此题dp[i] 就表示的是[0，i-1] 区间的和而不是之前的 0 ~ i 区间的和了，相应的，状态转移方程也要有所变化

同时这道题还需要求一个后缀和数组用来描述后半段的区间和，也是同样的道理，只不过 dp[i] 表示的是[i + 1，n - 1] 区间的和，这段区间的状态转移方程也就是 dp[i+1] + nums[i + 1]

class Solution {public int pivotIndex(int[] nums) {int n = nums.length;int[] dp = new int[n];int[] g = new int[n];for (int i = 1; i < n; i++) {dp[i] = dp[i - 1] + nums[i - 1];}for (int i = n - 2; i >= 0; i--) {g[i] = g[i + 1] + nums[i + 1];}for (int i = 0; i < n; i++) {if (g[i] == dp[i]) {return i;}}return -1;}
}

4. 除自身以外数组的乘积

238. 除自身以外数组的乘积

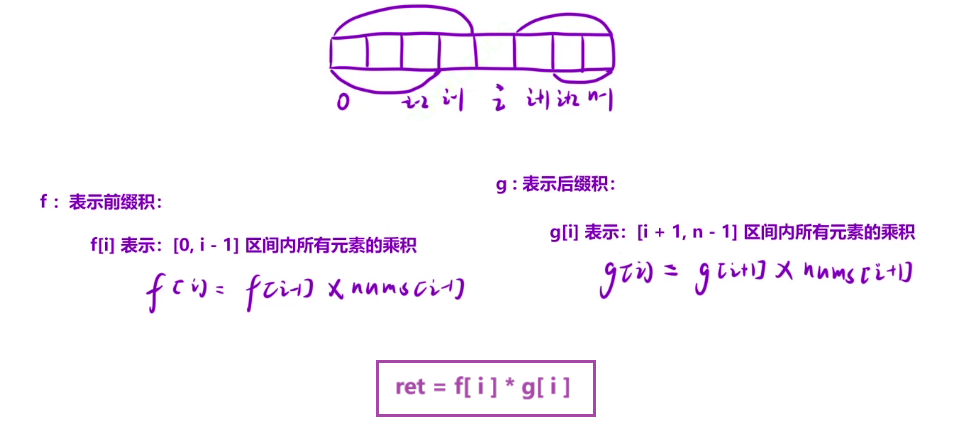
这道题其实就和上道题非常类似，把 i 位置之前的数都求一个前缀积，之后的数求一个后缀积，只需要把前缀积和后缀积相乘就可以了

class Solution {public int[] productExceptSelf(int[] nums) {int n = nums.length;int[] f = new int[n];int[] g = new int[n];int[] ans = new int[n];f[0] = 1;g[n - 1] = 1;for (int i = 1; i < n; i++) {f[i] = f[i - 1] * nums[i - 1];}for (int i = n - 2; i >= 0; i--) {g[i] = g[i + 1] * nums[i + 1];}for (int i = 0; i < n; i++) {ans[i] = f[i] * g[i];}return ans;}
}

5. 和为 K 的子数组

560. 和为 K 的子数组

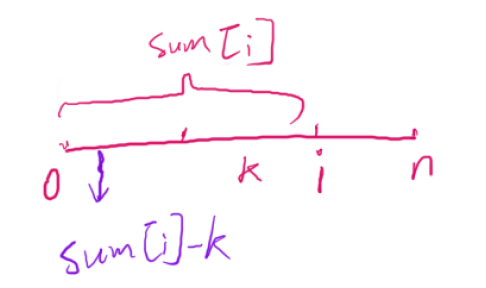
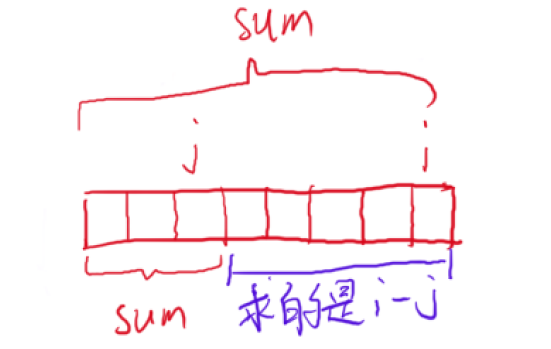
思路：每次都求0 ~ i - 1 区间内有多少个子数组是和为 k 的，如果正常求的话，时间复杂度就是O(n^2)了，所以说可以把子数组和为k的个数存在哈希表中去求，也就需要在求和的过程中就把这些数据添加到哈希表中，而求0 ~ i - 1 区间，和为 k 的子数组，就可以转化为求前半部分的哪段区间的和为整段区间和 sum - k

注意点：

1. 不用真正的创建一个前缀和数组去表示和，只需要用一个 sum 变量来计算即可
2. 如果说整个前缀和都等于k的话，就代表 sum - k 等于 0，这个需要提前在哈希表中存储，因为此时需要在 0~-1 区间内去找一个和为0的次数，但是这个区间不存在，所以说需要提前设置为 1，当需要查找的时候，就是默认的 1
3. 前缀和加入到哈希表的时机：需要在计算i位置之前，保存0~i-1区间的前缀和，也就是知道 sum - k的次数，i-1统计之后才可以把i位置的前缀和存入哈希表中

class Solution {public int subarraySum(int[] nums, int k) {int sum = 0,ret = 0;HashMap<Integer,Integer> hash = new HashMap<>();hash.put(0,1);for(int x : nums){sum+=x;//以当前元素为结尾时有多少符合条件的答案ret+=hash.getOrDefault(sum - k,0);hash.put(sum,hash.getOrDefault(sum,0) + 1);}return ret;}
}

6. 和可被 K 整除的子数组

974. 和可被 K 整除的子数组

同余定理：(a - b) / p = k......0 => a % p = b % p

就是如果 a - b 的差能够被 p 整除的话，那么 a 和 b 对 p 取模就相等

在 Java 中，一个负数对一个正数取模的话得到的是一个负数，如果想要修正为正数的话可以使用下面的式子

首先把负数的余数变为正数，但如果原来就是正数的话还是不对的，所以需要再取一个余数

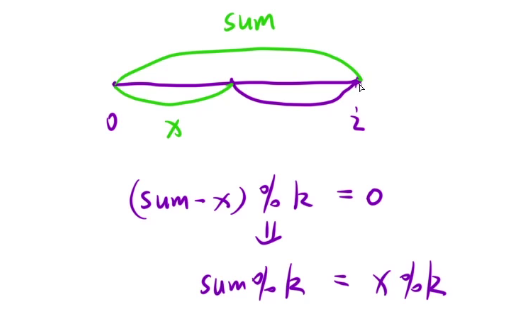
这样就可以把题目转化为只需要求在 i 之前有多少个区间对 K 取模之后等于 0 ，也就和上一题类似了

class Solution {public int subarraysDivByK(int[] nums, int k) {int sum = 0, ret = 0;HashMap<Integer, Integer> hashMap = new HashMap<>();hashMap.put(0 % k, 1);for (int x : nums) {sum += x;int r = (sum % k + k)% k;ret += hashMap.getOrDefault( r, 0);hashMap.put(r, hashMap.getOrDefault(r, 0) + 1);}return ret;}
}

7. 连续数组

525. 连续数组

如果直接统计 0 和 1 的个数的话还是比较麻烦的，可以转化一下，把所有的 0 都变成 - 1，当 0 和 1 的个数相等时，也就是区间和等于 0 的情况，也就转化为了之前的求和为 k 的子数组的问题，只不过之前求的是个数，这题求的是长度，

class Solution {public int findMaxLength(int[] nums) {HashMap<Integer, Integer> hash = new HashMap<>();hash.put(0, -1);int sum = 0, ret = 0;for (int i = 0; i < nums.length; i++) {sum += (nums[i] == 0 ? -1 : 1);if (hash.containsKey(sum)) {ret = Math.max(ret, i - hash.get(sum));} else {hash.put(sum, i);}}return ret;}
}

需要注意的是，如果说在之后发现有重复的 sum 的时候，就不需要再存放进哈希表中了，因为此时的长度肯定是没有第一次的长的，就会影响后面使用 i - j 时计算的长度

8. 矩阵区域和

1314. 矩阵区域和

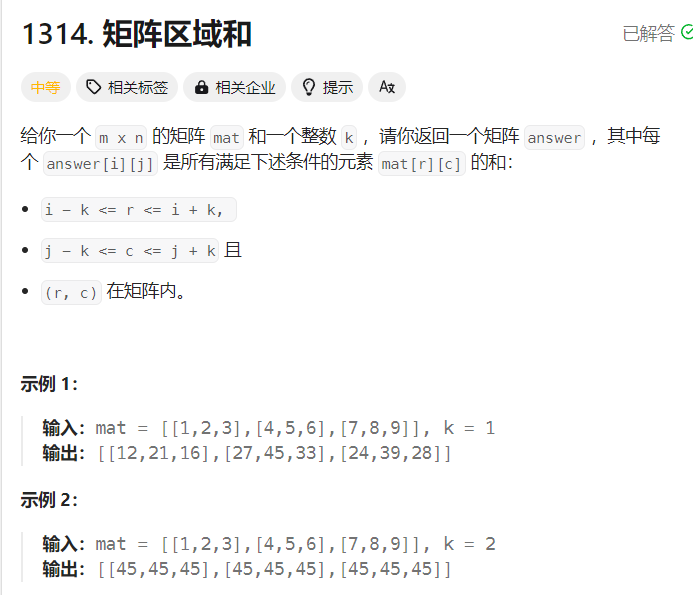
也就是周围所有元素的和

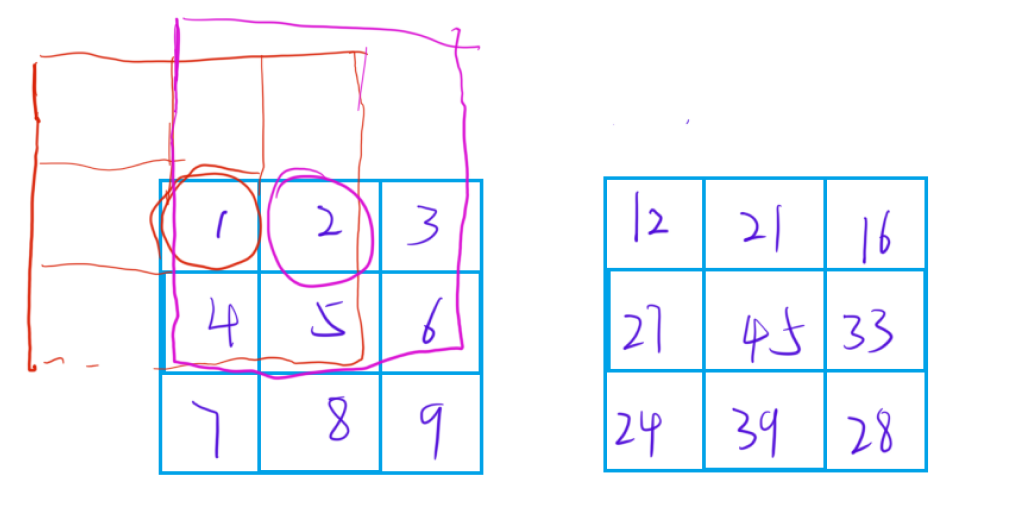
首先就是先预处理一个二维前缀和数组，然后再求( i , j ) 位置的值

求（i , j ）位置的值的时候和之前讲的前缀和模版类似

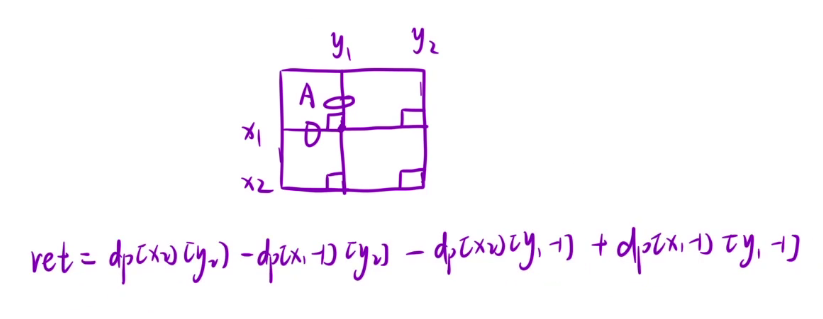
然后就是怎么求坐标的问题，知道（i , j）坐标之后，求此处的值的话就需要求左上角和右下角的坐标，然后才能求出这个区域中的元素和

关于下标的映射关系，由于题目中的数组是从下标 0 计算的，为了方便是将 dp 表从下标为 1 开始计算的，所以说后续再继续从 dp 表中使用值的时候是需要把 x ，y 坐标都加上 1 的

class Solution {public int[][] matrixBlockSum(int[][] mat, int k) {int m = mat.length, n = mat[0].length;int[][] dp = new int[m + 1][n + 1];int[][] ans = new int[m][n];for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j-1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];}}for(int i = 0; i< m;i++){for(int j = 0;j < n;j++){int x1 = Math.max(0,i - k) + 1,y1 = Math.max(0,j - k) + 1;int x2 = Math.min(m - 1,i + k) + 1,y2 = Math.min(n - 1, j + k) + 1;ans[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];}}return ans;}
}