【C++】模拟实现红黑树
🦄个人主页:修修修也
🎏所属专栏:实战项目集
⚙️操作环境:Visual Studio 2022

目录
一.了解项目功能
二.逐步实现项目功能模块及其逻辑详解
📌实现RBTreeNode类模板
🎏构造RBTreeNode类成员变量
🎏实现RBTreeNode类构造函数
📌实现RBTree类模板
🎏构造RBTree类成员变量
🎏实现RBTree类构造函数
🎏实现RBTree插入函数
🎏实现RBTree插入左单旋(和AVL树一样)
🎏实现RBTree插入右单旋(和AVL树一样)
🎏判断红黑树是否符合红黑树规则函数
三.项目完整代码
test.c文件
RBTree.h文件
结语
一.了解项目功能
在本次项目中我们的目标是实现一个红黑树类模板,还不了解红黑树概念的朋友可以先移步[【数据结构】什么是红黑树(Red Black Tree)?]其结构图示如下:

红黑树结点(RBTreeNode)需要包含五个成员:键值对_kv, 左指针域_left, 右指针域_right, 父亲指针域_parent, 颜色标识_col.结点(RBTreeNode)逻辑结构图示如下:
红黑树类模板提供的功能有:
- 红黑树结点类的构造函数
- 红黑树的构造函数
- 红黑树的插入函数
- 左单旋函数
- 右单旋函数
- 判断红黑树是否符合红黑树规则函数
二.逐步实现项目功能模块及其逻辑详解
通过第二部分对项目功能的介绍,我们已经对 的功能有了大致的了解,虽然看似需要实现的功能很多,貌似一时间不知该如何下手,但我们可以分步分模块来分析这个项目的流程,最后再将各部分进行整合,所以大家不用担心,跟着我一步一步分析吧!
!!!注意,该部分的代码只是为了详细介绍某一部分的项目实现逻辑,故可能会删减一些与该部分不相关的代码以便大家理解,需要查看或拷贝完整详细代码的朋友可以移步本文第四部分。
📌实现RBTreeNode类模板
🎏构造RBTreeNode类成员变量
我们在一开始需求分析时就已经明确了红黑树结点(RBTreeNode)需要包含五个成员:键值对_kv, 左指针域_left, 右指针域_right, 父亲指针域_parent, 颜色标识_col.结点(RBTreeNode)逻辑结构图示如下:
对于颜色标识符,我们可以设置一个枚举来标识红色和黑色,增加代码的可读性:
enum Colour {RED,BLACK };
这里还有一个小的点需要提一下,我们在这里实现的RBTreeNode类,后续是要给RBTree类使用的,考虑到后续我们在红黑树的操作函数中会有直接操作结点成员变量的情况,如:
cur->_left = root->_right; //相当于在RBTreeNode外部直接通过类指针访问了类成员变量_left基于class的封装特性,class的成员变量一般都是默认为私有的,如果我们要允许其他类直接访问class的成员变量和函数,就要将其都设置为public,或者通过友元/内部类来解决成员访问问题.
既然如此,我们不妨直接使用struct定义结点成员变量和函数,因为struct定义的类的成员变量和函数默认就是公有的,完全可以满足我们的需求.
综上所述,该部分代码如下:
template<class K,class V> struct RBTreeNode {RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col; };
🎏实现RBTreeNode类构造函数
RBTreeNode的构造函数我们实现两个即可,一个是有参构造,一个是无参构造,而无参构造又可以通过给缺省值的方式和有参构造合二为一,所以我们用初始化列表来实现一下RBTreeNode的构造函数(我在红黑树的概念中已经分析过为什么新插入的结点一定是红色,这里就不多赘述了):
//缺省值的作用是在无参调用时直接去调用模板实例化的类的无参构造函数 //这里一定不能将缺省值给0/nullptr!因为你不知道模板实例化的类具体到底是内置类型还是自定义类型(如Date) //所以要显示调用pair<K,V>类型它自己的无参构造函数RBTreeNode(const pair<K,V>& kv=pair<K,V>()):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED) {}
📌实现RBTree类模板
🎏构造RBTree类成员变量
RBTree类成员变量比较简单,就是一个根节点的指针,为了简化模板中出现的RBTreeNode<K,V>类型的名字,我们将其简化命名为:Node
该部分实现代码如下:
template<class K,class V> class RBTree {typedef RBTreeNode<K,V> Node;private:Node* _root; };
🎏实现RBTree类构造函数
RBTree类的构造函数非常简单,因为只有一个成员变量根节点指针_root,所以我们用初始化列表将该结点指针初始话为nullptr即可,代码如下:
RBTree():_root(nullptr) {}
🎏实现RBTree插入函数
RBTree类的插入函数实现思路如下:
如果我们遇到了插入后违反红黑树规则的情况,那么红黑树的调整规则如下:
- 插入结点是根节点(即破坏了根节点是黑色的规则)--->解决方法,直接将该节点变黑
- 插入结点的父节点也是红色(即破坏了红结点的孩子必须是黑色的规则),分两种情况
- 插入结点的叔叔结点是红色: 将叔叔和父亲变为黑色, 爷爷结点变为红色, 然后继续向上判定爷爷结点是否违反了红黑树的规则并进行调整
- 插入结点的叔叔结点不存在或是黑色: 根据形态进行相应的旋转操作,旋转完成后,将旋转后的根节点变黑,将祖父结点变红即可
综上所述,红黑树的插入函数代码实现如下:
bool Insert(const pair<K, V>& kv) {//前期的插入逻辑就是二叉搜索树的插入逻辑if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//找插入位置Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//插入新结点cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){//插右边parent->_right = cur;}else{//插左边parent->_left = cur;}cur->_parent = parent;//控制红黑树的特性...控制颜色//插入的永远是红结点//插入的是根,把结点变红//插入时父节点是黑,就ok了//插入的父节点是红,看叔叔// 叔叔是红,把父亲叔叔都变黑,把爷爷变红(然后继续向上处理)// 叔叔是黑,旋转,转完父爷都变色while ( parent && parent->_col == RED && parent->_parent){Node* grandfather = parent->_parent;//因为我们在红黑树中不用平衡因子但是要判断是LL/RR/LR/RL型的旋转,因此需要在这里分情况讨论if (parent == grandfather->_left){Node* uncle = grandfather->_right;//叔叔存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上处理cur = grandfather;parent = cur->_parent;}else//叔叔不存在或存在且为黑,就旋转{if (cur == parent->_left){RotateR(grandfather);//转完换色parent->_col = BLACK;grandfather->_col = RED;}else{RotateL(parent);RotateR(grandfather);//转完换色cur->_col = BLACK;grandfather->_col = RED;}}}else//parent == grandfather->_right{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){RotateR(parent);RotateL(grandfather);//改色cur->_col = BLACK;grandfather->_col = RED;}else{RotateL(grandfather);//祖父一定是红色,父子谁最后旋到根谁变黑//单旋父黑,双旋子黑//单旋爷变子,双旋子变父parent->_col = BLACK;grandfather->_col = RED;}}}}_root->_col = BLACK;return true; }
🎏实现RBTree插入左单旋(和AVL树一样)
左单旋处理应用的情况为:
- 插入结点是父亲结点的右孩子
- 父亲结点是爷爷结点的右孩子
左单旋的处理操作步骤为:
- 将父亲结点的左子树链接到爷爷结点的右孩子的位置
- 将爷爷链接到父亲结点的左孩子位置
综上,实现代码及详解如下:
//左单旋void RotateL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;Node* ppnode = parent->_parent;//将失衡结点右孩子的左子树链接到失衡结点的右孩子parent->_right = curleft;if (curleft){curleft->_parent = parent;}//将失衡结点连接到失衡结点右孩子的左孩子位置parent->_parent = cur;cur->_left = parent;//处理父父结点的链接cur->_parent = ppnode;if (ppnode == nullptr)//为空代表parent就已经是root了{_root = cur;}else{if (ppnode->_left == parent)//失衡结点是其父节点的左孩子{ppnode->_left = cur;}else //失衡结点是其父节点的右孩子{ppnode->_right = cur;}}}
🎏实现RBTree插入右单旋(和AVL树一样)
右单旋处理应用的情况为:
- 插入结点是父亲结点的左
- 父亲结点是爷爷结点的左
右单旋的处理操作步骤为:
- 将父亲结点的右子树链接到爷爷结点的左孩子的位置
- 将爷爷结点链接到父亲结点的右孩子位置
综上,实现代码及详解如下:
//右单旋void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;Node* ppnode = parent->_parent;//将失衡结点左孩子的右子树连接到失衡结点的左孩子位置parent->_left = curright;if (curright){curright->_parent = parent;}//将失衡结点连接到失衡结点左孩子的右孩子位置parent->_parent = cur;cur->_right = parent;//链接父父结点cur->_parent = ppnode;if (ppnode == nullptr)//为空代表parent就已经是root了{_root = cur;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}}}
🎏判断红黑树是否符合红黑树规则函数
判断一棵树是不是红黑树,就要从红黑树的几个规则出发,看其是否满足下面这几个规则:
- 每个结点不是红色就是黑色
- 根结点是黑色
- 如果一个结点是红色的,则它的子结点一定是黑色
- 任一结点到NULL(树尾)的任何路径上,所含的黑色结点数一定相同
- 每个NULL(树尾)空结点都是黑色的
综上,实现代码如下:
//检查结点是否满足没有连续的两个红结点,以及所有路径的黑节点数量都相同函数 bool CheckColour(Node* root, int blacknum, int benchmark) {if (root == nullptr){if (benchmark != blacknum)return false;return true;}//计算路径黑节点数量if (root->_col == BLACK){++blacknum;}//如果一个结点是红色,它的父亲也是红色,那就违反了没有两个连续红结点的规则if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_kv.first << "连续红结点" << endl;return false;}return CheckColour(root->_left,blacknum,benchmark)&& CheckColour(root->_right,blacknum,benchmark); }//RBTree验证函数递归子函数 bool _IsBalance(Node* root) {if (root == nullptr)return true;//规则:根节点是黑色if (root->_col != BLACK)return false;//求黑节点基准值(用左路的黑节点数量来计算)int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)benchmark++;cur = cur->_left;}//规则:不能有连续的红结点,且每条路径黑节点数量相同return CheckColour(root, 0, benchmark); }//RBTree验证函数(嵌套的目的是为了方便传参) bool IsBalance() {return _IsBalance(_root); }
三.项目完整代码
我们将程序运行的代码分别在三个工程文件中编辑,完整代码如下:
test.c文件
该文件主要包含一些对AVL树的功能测试代码,大家可以酌情参考或自己编写测试用例:
#include"RBTree.h"void test1() {int a[] = { 16,3,7,11,9,26,18,14,15 };RBTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));cout << "Insert:" << e << "->" << t.IsBalance() << endl;} }void test2() {int a[] = { 14, 9, 5, 17, 11, 12, 7, 19, 16, 27 };RBTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));cout << "Insert:" << e << "->" << t.IsBalance() << endl;} }void test3() {int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));cout << "Insert:" << e << "->" << t.IsBalance() << endl;} }//随机数暴力测试 void test4() {const int N = 1000000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand());}cout << "数据录入完毕,开始插入" << endl;RBTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}cout << t.IsBalance() << endl;t.InOrder();cout << "插入结束" << endl; }int main() {test4();return 0; }
RBTree.h文件
#pragma once#include<iostream>
#include<vector>
using namespace std;enum Colour
{RED,BLACK
};template<class K,class V>
struct RBTreeNode
{RBTreeNode(const pair<K,V>& kv=pair<K,V>()):_left(nullptr),_right(nullptr),_parent(nullptr),_kv(kv),_col(RED){}RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;
};template<class K,class V>
class RBTree
{typedef RBTreeNode<K,V> Node;
public:RBTree():_root(nullptr){}bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;while (cur)//查了半天是这里少写了个循环...(好在自己查到了,去比对了一下,果然...加上就好了{if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){//插右边parent->_right = cur;}else{//插左边parent->_left = cur;}cur->_parent = parent;//...控制颜色//插入的永远是红结点//插入的是根,把结点变红//插入时父节点是黑,就ok了//插入的父节点是红,看叔叔// 叔叔是红,把父亲叔叔都变黑,把爷爷变红(然后继续向上处理)// 叔叔是黑,旋转,转完父爷都变色while ( parent && parent->_col == RED && parent->_parent){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//叔叔存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上处理cur = grandfather;parent = cur->_parent;}else//叔叔不存在或存在且为黑,就旋转{if (cur == parent->_left){RotateR(grandfather);//转完换色parent->_col = BLACK;grandfather->_col = RED;}else{RotateL(parent);RotateR(grandfather);//转完换色cur->_col = BLACK;grandfather->_col = RED;}}}else//parent == grandfather->_right{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){RotateR(parent);RotateL(grandfather);//改色cur->_col = BLACK;grandfather->_col = RED;}else{RotateL(grandfather);//祖父一定是红色,父子谁最后旋到根谁变黑//单旋父黑,双旋子黑//单旋爷变子,双旋子变父parent->_col = BLACK;grandfather->_col = RED;}}}}_root->_col = BLACK;return true;}//左单旋void RotateL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;Node* ppnode = parent->_parent;//将失衡结点右孩子的左子树链接到失衡结点的右孩子parent->_right = curleft;if (curleft){curleft->_parent = parent;}//将失衡结点连接到失衡结点右孩子的左孩子位置parent->_parent = cur;cur->_left = parent;//处理父父结点的链接cur->_parent = ppnode;if (ppnode == nullptr)//为空代表parent就已经是root了{_root = cur;}else{if (ppnode->_left == parent)//失衡结点是其父节点的左孩子{ppnode->_left = cur;}else //失衡结点是其父节点的右孩子{ppnode->_right = cur;}}}//右单旋void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;Node* ppnode = parent->_parent;//将失衡结点左孩子的右子树连接到失衡结点的左孩子位置parent->_left = curright;if (curright){curright->_parent = parent;}//将失衡结点连接到失衡结点左孩子的右孩子位置parent->_parent = cur;cur->_right = parent;//链接父父结点cur->_parent = ppnode;if (ppnode == nullptr)//为空代表parent就已经是root了{_root = cur;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}}}//中序遍历函数void InOrder(){_InOrder(_root); //代替成员函数完成递归cout << endl; //方便后续观察测试用例}//中序遍历子递归函数void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left); //递归访问左子树cout << root->_kv.first << " "; //访问根节点_InOrder(root->_right); //递归访问右子树}//验证双红结点和路径黑结点数是否相同函数bool CheckColour(Node* root, int blacknum, int benchmark){if (root == nullptr){if (benchmark != blacknum)return false;return true;}if (root->_col == BLACK){++blacknum;}if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_kv.first << "连续红结点" << endl;return false;}return CheckColour(root->_left,blacknum,benchmark)&& CheckColour(root->_right,blacknum,benchmark);}bool IsBalance(){return _IsBalance(_root);}//RBTree验证函数bool _IsBalance(Node* root){if (root == nullptr)return true;//规则:根节点是黑色if (root->_col != BLACK)return false;//求黑节点基准值int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)benchmark++;cur = cur->_left;}//规则:不能有连续的红结点,且每条路径黑节点数量相同return CheckColour(root, 0, benchmark);}private:Node* _root;
};结语
希望这篇红黑树的实现详解能对大家有所帮助,欢迎大佬们留言或私信与我交流.
学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!
相关文章推荐
【C++】模拟实现AVL树
【数据结构】什么是平衡二叉搜索树(AVL Tree)?
【C++】STL标准模板库容器map
【C++】STL标准模板库容器set
【C++】模拟实现二叉搜索(排序)树
【数据结构】C语言实现链式二叉树(附完整运行代码)
【数据结构】什么是二叉搜索(排序)树?
【C++】模拟实现priority_queue(优先级队列)
【C++】模拟实现queue
【C++】模拟实现stack
【C++】模拟实现list
【C++】模拟实现vector
【C++】标准库类型vector
【C++】模拟实现string类
【C++】标准库类型string
【C++】构建第一个C++类:Date类
【C++】类的六大默认成员函数及其特性(万字详解)
【C++】什么是类与对象?

相关文章:

【C++】模拟实现红黑树
🦄个人主页:修修修也 🎏所属专栏:实战项目集 ⚙️操作环境:Visual Studio 2022 目录 一.了解项目功能 二.逐步实现项目功能模块及其逻辑详解 📌实现RBTreeNode类模板 🎏构造RBTreeNode类成员变量 🎏实现RBTreeNode类构…...

离线安装docker
背景描述 项目需要在研发环境虚拟机上安装docker部署应用。 所在的服务器是一个内网,无法访问到外网环境。 服务器OS版本是 麒麟V10 linux 安装docker 安装包下载 获取所需版本的docker binary包,官方链接https://download.docker.com/linux/stati…...

MySQL高阶2066-账户余额
目录 题目 准备数据 分析数据 总结 题目 请写出能够返回用户每次交易完成后的账户余额. 我们约定所有用户在进行交易前的账户余额都为0, 并且保证所有交易行为后的余额不为负数。 返回的结果请依次按照 账户(account_id), 日期( day ) 进行升序排序…...
《RabbitMQ篇》Centos7安装RabbitMQ
安装RabbitMQ 安装包网盘下载地址 链接:https://pan.baidu.com/s/1bG_nP0iCdAejkctFp1QztQ?pwd4mlw 先上传安装包到服务器(erlang-23.3.4.11-1.el7.x86_64.rpm和rabbitmq-server-3.9.16-1.el7.noarch.rpm)然后使用指令安装 # 安装 erlang r…...

昇思学习打卡营第31天|深度解密 CycleGAN 图像风格迁移:从草图到线稿的无缝转化
1. 简介 图像风格迁移是计算机视觉领域中的一个热门研究方向,其中 CycleGAN (循环对抗生成网络) 在无监督领域取得了显著的突破。与传统需要成对训练数据的模型如 Pix2Pix 不同,CycleGAN 不需要严格的成对数据,只需两类图片域数据,…...

跟我学C++中级篇——空值的定义
一、空值 在提到c/c的空值时,先扯远一些。谈一谈数学中的0,0的出现要晚于其它的数,而0的出现却引发了数学的极大的发展和进步。而在计算机科学中,在使用一个变量时,它的值的可能性有很多,其中,…...
Mysql 数据库系统全解析)
(三)Mysql 数据库系统全解析
一、Mysql 数据库 数据库的作用和优势 作用:集中化存储结构性的数据。优势: 减小数据冗余,避免数据的重复存储。保证数据的真实有效和唯一性,提高数据的质量。方便数据共享访问,使得不同的用户和应用可以方便地获取所需…...
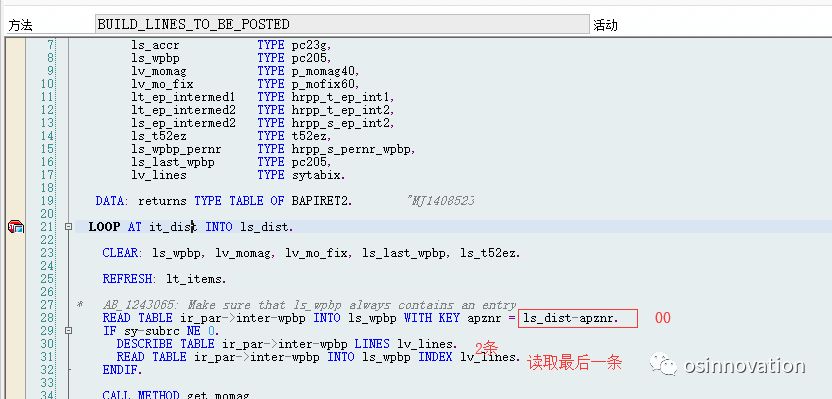
SAP HCM 0001信息类型一个月内有多个成本中心
一般跨部门调动时候,成本中心都会变化,SAP默认都是读取wpbp的最后一一条数据,但是今天过账会读取两个单位的成本中心,一直都觉得很奇怪,SAP如何都拆分出这样的情况, 没办法只有debug,初始化系统…...

字节输入流
1.是什么 字节输入流(Byte Input Stream)在Java中是用来读取原始字节流的数据。Java的java.io包提供了多种字节输入流类,其中InputStream是所有字节输入流类的超类。以下是关于字节输入流的详细解释和举例: 字节输入流的概念&…...

深度学习-----------------机器翻译与数据集
目录 机器翻译与数据集下载和预处理数据集预处理步骤词元化词汇表该部分总代码 固定长度阶段或填充该部分总代码 转换成小批量数据集用于训练训练模型总代码 机器翻译与数据集 import os import torch from d2l import torch as d2l下载和预处理数据集 #save d2l.DATA_HUB[fr…...

SOMEIP_ETS_151: SD_Send_triggerEventUINT8Reliable_Eventgroup_2
测试目的: 验证DUT在Tester订阅事件组后,能够响应Tester触发的triggerEventUINT8Reliable方法,并将TestEventUINT8Reliable事件发送到订阅请求中端点选项指定的IP地址和端口。 描述 本测试用例旨在确保DUT能够正确处理事件组的订阅请求&am…...

32 C 语言指针的长度与运算(指针加减整数、指针自增自减、同类型指针相减、指针的比较运算)
目录 1 指针的长度 2 指针与整数的加减运算 3 指针自增与自减 4 同类型指针相减 5 指针的比较运算 6 测试题 1 指针的长度 在 C 语言中,sizeof 运算符可以用来计算指针的长度。指针的长度实际上与指针所指向的数据类型无关,而是与系统的位数&…...

【系统架构设计师】经典论文:轮软件三层架构设计
更多内容请见: 备考系统架构设计师-核心总结目录 文章目录 摘要正文总结摘要 本人于 2022 年 1 月参与了中石化 XX 油田 XX 采油厂“用电管理系统”的项目建设,该系统建设目标是实现分单位、分线路、分系统评价、优化、考核,全面提升采油厂用 电管理水平。在该项目组中我担…...

(C语言贪吃蛇)13.实现贪吃蛇四方向的移动
目录 前言 原代码预览 解决方法⚠️ 运行效果 总结 前言 我们上节通过Linux线程实现了两个while(1)同时运行,这样就可以一边控制方向一遍刷新出贪吃蛇的身体节点了。本节我们就来实现贪吃蛇四方向的移动。 (此图片为最终效果) 原代码预览 我们之前的代码是通过…...
)
Spring Boot + MyBatis 项目中常用注解详解(万字长篇解读)
Spring Boot MyBatis 项目中常用注解详解 在现代Java开发中,Spring Boot和MyBatis是两大热门框架,广泛应用于构建高效、可维护的企业级应用。两者结合使用,可以充分发挥各自的优势,提高开发效率和代码质量。在这个过程中&#x…...

AWS Network Firewall -NAT网关配置只应许白名单域名出入站
1. 创建防火墙 选择防火墙的归属子网(选择公有子网) 2. 创建规则白名单域名放行 3. 绑定相关规则 继续往下拉 绑定非托管规则 4. 配置网络路由 相关规则 参考图 解释 防火墙的归属公有子网路由表规则机器实例的规则子网路由表规则nat网管路…...

【C语言系统编程】【第二部分:并发编程】2.3 实践与案例分析
2.3 实践与案例分析 2.3.1 案例分析:多线程文件搜索程序 本文中,我们将通过一个多线程文件搜索程序的案例,展示如何在实际项目中应用多线程编程技术,并具体介绍任务分解、线程创建、结果汇总及锁机制的应用。 2.3.1.1 任务分解…...

React -AppVarContext.Provider 提供者组件
AppVarContext.Provider 是一个 React 上下文提供者,通常用于在组件树中提供共享的状态或数据。下面将详细解释 AppVarContext.Provider 的作用和如何使用它。展示如何使用 AppVarContext.Provider 来管理全局状态 1. 什么是上下文(Context)…...

【Python】解密用户代理:使用 Python User Agents 库探索浏览器和设备信息
Python User Agents 是一个专为解析 User Agent 字符串而设计的 Python 库。它能够轻松识别访问设备的类型(如移动设备、桌面设备或平板),并获取设备、浏览器、操作系统等详细信息。借助它,开发者可以更好地了解访问用户的设备属性…...

以串口接口为例介绍关于BSP底层架构开发的迭代过程
以串口接口为例介绍关于BSP底层架构开发的迭代过程 文章目录 以串口接口为例介绍关于BSP底层架构开发的迭代过程架构概述初代BSP二代BSP:三代BSP:四代BSP:架构概述 单片机开发有四个阶段: 阶段一:单一单片机的功能实现阶段 此阶段你开始熟悉STM32F1系列的单片机,并利用…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...


