【笔记】选择题笔记+数据结构笔记
文章目录
- 2014 41
- 方法一先序遍历
- 方法二
连通分量是极大连通子图
一个连通图的生成树是一个极小连通子图
无向图的邻接表中,第i个顶点的度为第i个链表中的结点数
邻接表和邻接矩阵对不同的操作各有优势。
最短路径算法:
- 单源最短路径
已知图G=(V,E),我们希望找出从某给定的源结点S∈V到V中每个节点的最短路径
Dijkstra算法复杂度 O ( n 2 ) O(n^2) O(n2) - 全源最短路径
任意两个节点之间的最短路径
Floyd算法复杂度 O ( n 3 ) O(n^3) O(n3)
最小生成树Prim算法和Kruskal算法【O(mlogm)】
相关阅读资料
Prim算法通常以邻接矩阵作为储存结构。
时间复杂度在对数级别的时候,底数数字的改变对于整个时间复杂度没有影响
静态链表方便经常插入和删除
二叉排序树的中序序列才是有序的
二叉排序树左子树上的值均大于根节点的值,右子树的值均小于根节点的值【不仅仅是左孩子和右孩子】
新插入的关键字总是作为叶节点插入,叶节点不一定总是处于最底层
二叉排序树只有删除的是叶节点才能得到与原来一样的二叉排序树
2014 41
二叉树的带权路径长度(WPL)是二叉树中所有叶结点的带权路径长度之和。给定一棵二叉树T,采用二叉链表存储,结点结构为:

其中叶结点的weight域保存该结点的非负权值。设root为指向T的根结点的指针,请设计求T的WPL的算法,要求:(1)给出算法的基本设计思想; (2)使用C或C++语言,给出二叉树结点的数据类型定义; (3)根据设计思想,采用C或C++语言描述算法,关键之处给出注释。
方法一先序遍历
解决方法:考查二叉树的带权路径长度,二叉树的带权路径长度为每个叶子结点的深度与权值之积的总和,可以使用先序遍历或层次遍历解决问题。
(1)算法的基本设计思想基于先序递归遍历的算法思想是用一个static变量记录wpl,把每个结点的深度作为递归函数的一个参数传递,算法步骤如下:若该结点是叶子结点,那么变量wpl加上该结点的深度与权值之积,若该结点非叶子结点,那么若左子树不为空,对左子树调用递归算法,若右子树不为空,对右子树调用递归算法,深度参数均为本结点的深度参数加一;最后返回计算出的wpl即可。
(2)二叉树结点的数据类型定义如下:
#include<stdio.h>
#include<stdlib.h>typedef struct BiTiNode
{
int weight;
struct BiTiNode *lchild,*rchild;
}BiTiNode,*BiTree;
/**
二叉树数据结构定义
**/
int WPL(BiTree root){return wpl_PreOrder(root,1);
}
int wpl_PreOrder(BiTree root,int deep){static int wpl=0;//静态变量存储wpl 静态局部变量//作用域为这个函数//若为叶子结点if(root->left==NULL&& root->right==NULL)wpl+=deep*root->data;//若左子树不空,对左子树递归遍历if(root->left!=NULL)wpl_PreOrder(root->left,deep+1);//若右子树不空,对右子树进行递归遍历if(root->right!=NULL){wpl_PreOrder(root->right,deep+1);}return wpl;
}在先序遍历的算法中,static 是一个静态变量,只在首次调用函数时声明wpl并赋值为0,以后的递归调用并不会使得wpl为0。考虑到历年真题算法答案通常都直接仅仅由一个函数构成,所以参考答案使用static而不是全局变量。
方法二
(1)算法的基本设计思想基于层次遍历的算法思想是使用队列进行层次遍历,并记录当前的层数,当遍历到叶子结点时,累计wpl;当遍历到非叶子结点时对该结点的把该结点的子树加入队列;当某结点为该层的最后一个结点时,层数自增1; 队列空时遍历结束,返回wpl。
(2)二叉树结点的数据类型定义
int wpl_LevelOrder(BiTree root){BiTree q[MaxSize];int end1,end2;//end1 头指针,end2尾指针end1=end2=0;//头指针指向队头元素,尾指针指向队尾的后要给元素int wpl=0,deep=1;//初始化wpl和深度BiTree lastNode;//lastNode用来记录当前层的最后一个结点BiTree newlastNode;//newlastNode用来记录下一层的最后一个结点lastNode=root;//lastNode初始化为根结点newlastNode=NULL;//newlastNode初始化为空q[end2++]=root;///根节点入队while(end1!=end2){//层次遍历//若队列不空则循环BiTree t = q[end1++];//拿出队列中的头一个元素if(t->lchild==NULL&&t->rchild==NULL)wpl+=deep*t->weight;//若为叶子节点,统计wplif(t->lchild!=NULL){//若非叶子节点把左节点入队q[end2++] = t->lchild;newlastNode = t->lchild;}//并设下一层的最后一个结点为该结点的左节点if(t->rchild!=NULL){q[end2++]=t->rchild;newlastNode=t->rchild;}if(t==lastNode){//结点为本层最后一个结点。更新lastNode;lastNode=newlastNode;deep+=1;}}
return wpl;
}
相关文章:

【笔记】选择题笔记+数据结构笔记
文章目录 2014 41方法一先序遍历方法二 连通分量是极大连通子图 一个连通图的生成树是一个极小连通子图 无向图的邻接表中,第i个顶点的度为第i个链表中的结点数 邻接表和邻接矩阵对不同的操作各有优势。 最短路径算法: 单源最短路径 已知图G(V,E),我们…...
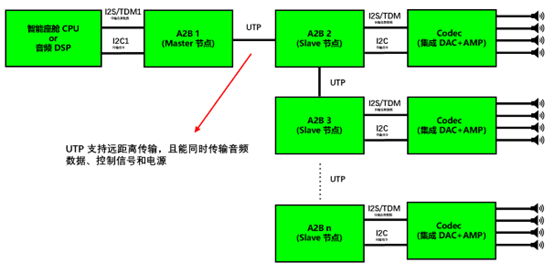
浅谈汽车智能座舱如何实现多通道音频
一、引言 随着汽车智能座舱的功能迭代发展,传统的 4 通道、6 通道、8 通道等音响系统难以在满足驾驶场景的需求,未来对于智能座舱音频质量和通道数会越来越高。接下来本文将浅析目前智能座舱如何实现音频功放,以及如何实现多路音频功放方案。…...

系统架构设计师教程 第13章 13.1层次式体系结构概述 笔记
13.1 层次式体系结构概述 分层式体系结构是一种最常见的架构设计方法,能有效地使设计简化,使设计的系统机构清晰,便于提高复用能力和产品维护能力。 层次式体系结构设计是将系统组成一个层次结构,每一层为上层服务,并…...
)
cnn突破一(先搞定三层反馈神经网络bpnet,c#实现)
惦记cnn很久了,一直搞机器视觉,走不出来,现在megauging已经实现,说明书也写了不少,该突破的突破了,该改进的也改进了,一个心病治好了,有空把人工智能在机器视觉上的延伸,…...

如何创建一个docker,给它命名,且下次重新打开它
1.创建一个新的docker并同时命名 docker run -it --name one ubuntu:18.04 /bin/bash 这时候我们已经创建了一个docker,并且命名为"one" 2.关闭当前docker exit 3.这时docker已经终止了,我们需要使用它要重新启动 docker start one 4.现在可以重新打…...

【D3.js in Action 3 精译_025】3.4 让 D3 数据适应屏幕(中)—— 线性比例尺的用法
当前内容所在位置(可进入专栏查看其他译好的章节内容) 第一部分 D3.js 基础知识 第一章 D3.js 简介(已完结) 1.1 何为 D3.js?1.2 D3 生态系统——入门须知1.3 数据可视化最佳实践(上)1.3 数据可…...

Python的多线程与多进程:并发编程基础与实战
随着计算机硬件的不断发展,现代计算机通常配备多核处理器,使得在程序中同时处理多个任务成为可能。并发编程是提升程序性能、充分利用多核处理器能力的重要技术之一。在Python中,并发编程的实现主要包括多线程、多进程以及异步编程(如asyncio)。然而,由于Python的全局解释…...

HarmonyOS Next应用开发——响应式布局之媒体查询
响应式布局之媒体查询 媒体查询作为响应式设计的核心,在移动设备上应用十分广泛。媒体查询可根据不同设备类型或同设备不同状态修改应用的样式,常用于多屏幕的应用适配。媒体查询常用于下面两种场景: 针对设备和应用的属性信息(…...

240 搜索二维矩阵 II
解题思路: \qquad 解这道题最重要的是如何利用从左到右、从上到下为升序的性质,快速找到目标元素。 \qquad 如果从左上角开始查找,如果当前matrix[i][[j] < target,可以向右、向下扩展元素都是升序,但选择哪个方向…...
jenkins微服务
如果vim进去某个文件里,可以按键盘的向下键查阅其它部分 记得每天备份虚拟机的项目 一.在linux安装jenkins 1.上传文件 我们采用安装包的方式安装。 先用SShclient在/usr/local/下创建jenkins文件夹,然后向其中导入两个包 2.安装jenkins 再在控制…...

【Kotlin基于selenium实现自动化测试】初识selenium以及搭建项目基本骨架(1)
导读大纲 1.1 Java: Selenium 首选语言1.2 配置一个强大的开发环境 1.1 Java: Selenium 首选语言 Java 是开发人员和测试人员进行自动化 Web 测试的首选 Java 和 Selenium 之间的协同作用受到各种因素的驱动,从而提高它们的有效性 为什么Java经常被认为是Selenium的首选语言 广…...

汽车追尾为什么是后车的责任?
简单点说:因为人后面没有长眼睛。 结论 在汽车追尾事故中,通常情况下后车被认为是责任方的原因在于交通法规对驾驶安全标准的约定和实践中的责任识别原则。虽然追尾事故常见地被归责于后车,但具体判断并不是绝对的,仍需综合多种…...

[运维]4.bookinfo无法部署的问题
为了拉取镜像,搭建了阿里云镜像仓库,教程见:K8S中基于NFS-Subdir-External-Provisioner存储组件实现的StorageClass-CSDN博客 但是bookinfo的ratings和productpage无法运行,部署后显示crashLoopBackOff [rootmaster ~]# kubectl…...

ACT调试pycharm报错
在运行ACT 代码时,根据官方readme使用命令行需要在wandb选择的时候输入3 但是,使用pycharm运行的时候会报错 wandb.errors.UsageError: api_key not configured (no-tty). call wandb.login(key[your_api_key]) 网上搜索都是说要注册什么key…...

记一次控件提升后,运行却不显示的Bug
.h文件 #ifndef VOLUMETOOLBTN_H #define VOLUMETOOLBTN_H#include <QToolButton> #include <memory>class VolumeToolBtn : public QToolButton { Q_OBJECTpublic:explicit VolumeToolBtn(QWidget *parent nullptr);~VolumeToolBtn() override;void initUi(); p…...

关于深度学习torch的环境配置问题
已经下好了torch在虚拟环境中,结果在ipynb文件中无法运行 后来在终端直接用python语句编译 发现没有问题 在编辑测试py文件 发现runcode有问题 原来是插件默认base环境 具体操作参考VS Code插件Code Runner使用python虚拟环境_coderunner怎么在虚拟环境中使用-CSD…...
Linux工具的使用——yum和vim的理解和使用
目录 linux工具的使用1.linux软件包管理器yum1.1yum的背景了解关于yum的拓展 1.2yum的使用 2.Linux编辑器-vim使用2.1vim的基本概念2.2vim的基本操作2.3命令模式命令集2.3.1关于光标的命令:2.3.2关于复制粘贴的命令2.3.3关于删除的命令2.3.4关于文本编辑的命令 2.4插…...
)
websockets库使用(基于Python)
主要参考资料: 【Python】websockets库的介绍及用法: https://blog.csdn.net/qq_53871375/article/details/135920231 python模块websockets,浏览器与服务器之间的双向通信: https://blog.csdn.net/randy521520/article/details/134752051 目录 websocke…...

Electron 主进程与渲染进程、预加载preload.js
在 Electron 中,主要控制两类进程: 主进程 、 渲染进程 。 Electron 应⽤的结构如下图: 如果需要更深入的了解electron进程,可以访问官网 流程模型 文档。 主进程 每个 Electron 应用都有一个单一的主进程,作为应用…...

鸿蒙harmonyos next纯flutter开发环境搭建
公司app是用纯flutter开发的,目前支持android和iOS,后续估计也会支持鸿蒙harmonyos。目前谷歌flutter并没有支持咱们国产手机操作系统鸿蒙harmonyos,于是乎国内有个叫OpenHarmony-SIG的组织,去做了鸿蒙harmonyos适配flutter开发的…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...
