代码随想录算法训练营第四十八天| 198 打家劫舍 213 打家劫舍II 337 打家劫舍III
代码随想录算法训练营第四十八天| 198 打家劫舍 213 打家劫舍II 337 打家劫舍III
LeetCode 198 打家劫舍
题目: 198.打家劫舍
动规五部曲:
- 确定dp数组以及下标的含义
dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷窃的金额为dp[i]。
- 确定递推公式
决定dp[i]的因素就是第i房间偷还是不偷。
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1])
- dp数组如何初始化
dp[0] 是 nums[0],dp[1]是nums[0]和nums[1]的最大值
即:dp[1] = max(nums[0], nums[1])
vector<int> dp(nums.size());
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
- 确定遍历顺序
dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的,从前到后遍历!
for (int i = 2; i < nums.size(); i++) {dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
- 举例来推导dp数组
整体代码:
class Solution {
public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];vector<int> dp(nums.size());dp[0] = nums[0];dp[1] = max(nums[0], nums[1]);for (int i = 2; i < nums.size(); i++) {dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[nums.size() - 1];}
};
LeetCode 213 打家劫舍II
题目: 213.打家劫舍II
此题与上题区别是有成环的情况,主要分为:
- 情况一:考虑不包含首尾元素
- 情况二:考虑包含首元素,不包含尾元素
- 情况三:考虑包含尾元素,不包含首元素
整体代码:
class Solution {
public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];int result1 = robRange(nums, 0, nums.size() - 2); // 情况二int result2 = robRange(nums, 1, nums.size() - 1); // 情况三return max(result1, result2);}// 198.打家劫舍的逻辑int robRange(vector<int>& nums, int start, int end) {if (end == start) return nums[start];vector<int> dp(nums.size());dp[start] = nums[start];dp[start + 1] = max(nums[start], nums[start + 1]);for (int i = start + 2; i <= end; i++) {dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[end];}
};
LeetCode 337 打家劫舍III
题目: 337.打家劫舍III
本题换成了树,首先想到遍历方式
本题一定要后序遍历,需要通过递归函数的返回值来做下一步计算。
- 确定递归函数的参数和返回值
vector<int> robTree(TreeNode* cur)
本题dp数组是一个长度为2的数组
- 确定终止条件
在遍历的过程中,如果遇到空节点的话,很明显,无论偷还是不偷都是0,返回
if (cur == NULL) return vector<int>{0, 0};
- 确定遍历顺序
使用后序遍历。通过递归函数的返回值来做下一步计算。
通过递归左节点,得到左节点偷与不偷的金钱。
通过递归右节点,得到右节点偷与不偷的金钱。
// 下标0:不偷,下标1:偷
vector<int> left = robTree(cur->left); // 左
vector<int> right = robTree(cur->right); // 右
// 中
- 确定单层递归的逻辑
如果偷当前节点,左右孩子不能偷,val1 = cur->val + left[0] + right[0];
如果不偷当前节点,左右孩子可以偷,选一个最大的:val2 = max(left[0], left[1]) + max(right[0], right[1]);
当前节点的状态就是{val2, val1}; 即:{不偷当前节点得到的最大金钱,偷当前节点得到的最大金钱}
vector<int> left = robTree(cur->left); // 左
vector<int> right = robTree(cur->right); // 右// 偷cur
int val1 = cur->val + left[0] + right[0];
// 不偷cur
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
return {val2, val1};
- 举例推导dp数组
整体代码:
class Solution {
public:int rob(TreeNode* root) {vector<int> result = robTree(root);return max(result[0], result[1]);}// 长度为2的数组,0:不偷,1:偷vector<int> robTree(TreeNode* cur) {if (cur == NULL) return vector<int>{0, 0};vector<int> left = robTree(cur->left);vector<int> right = robTree(cur->right);// 偷cur,那么就不能偷左右节点。int val1 = cur->val + left[0] + right[0];// 不偷cur,那么可以偷也可以不偷左右节点,则取较大的情况int val2 = max(left[0], left[1]) + max(right[0], right[1]);return {val2, val1};}
};
相关文章:

代码随想录算法训练营第四十八天| 198 打家劫舍 213 打家劫舍II 337 打家劫舍III
代码随想录算法训练营第四十八天| 198 打家劫舍 213 打家劫舍II 337 打家劫舍III LeetCode 198 打家劫舍 题目: 198.打家劫舍 动规五部曲: 确定dp数组以及下标的含义 dp[i]:考虑下标i(包括i)以内的房屋,最多可以偷…...
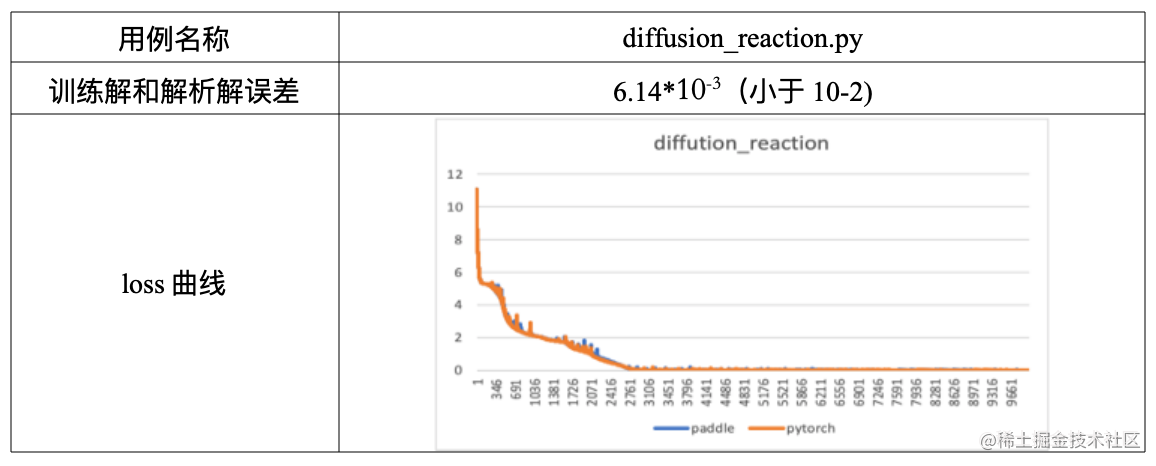
飞桨DeepXDE用例验证及评估
在之前发布的文章中,我们介绍了飞桨全量支持业内优秀科学计算深度学习工具 DeepXDE。本期主要介绍基于飞桨动态图模式对 DeepXDE 中 PINN 方法用例实现、验证及评估的具体流程,同时提供典型环节的代码,旨在帮助大家更加高效地基于飞桨框架进行…...

telegram连接本地Proxy连接不上
1.ClashX开启允许局域网连接。 2.重启ClashX和Telegram...
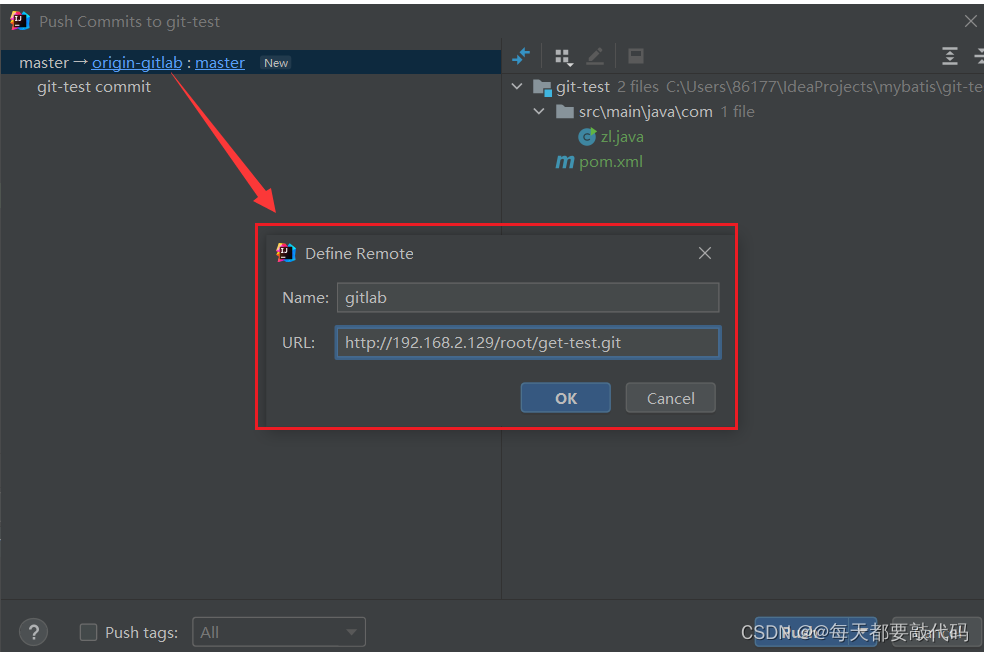
【分布式版本控制系统Git】| 国内代码托管中心-Gitee、自建代码托管平台-GitLab
目录 一:国内代码托管中心-码云 1. 码云创建远程库 2. IDEA 集成码云 3. 码云复制 GitHub 项目 二:自建代码托管平台-GitLab 1. GitLab 安装 2. IDEA 集成 GitLab 一:国内代码托管中心-码云 众所周知,GitHub 服务器在国外&…...
【面试】BIO、NIO、AIO面试题
文章目录什么是IO在了解不同的IO之前先了解:同步与异步,阻塞与非阻塞的区别什么是BIO什么是NIO什么是AIO什么NettyBIO和NIO、AIO的区别IO流的分类按照读写的单位大小来分:按照实际IO操作来分:按照读写时是否直接与硬盘,…...

C语言实现拼图求解
题目: 有如下的八种拼图块,每块都是由八块小正方块构成, 这些拼图块刚好可以某种方式拼合放入给定的目标形状, 请以C或C++编程,自动求解 一种拼图方式 目标拼图: 本栏目适合想要深入了解无向图、深度优先算法、编程语句如何实现算法、想要去接拼图算法的小伙伴。...

python --获取本机屏幕分辨率
pywin32 方法一 使用 win32api.GetDeviceCaps() 方法来获取显示器的分辨率。 使用 win32api.GetDC() 方法获取整个屏幕的设备上下文句柄,然后使用 win32api.GetDeviceCaps() 方法获取水平和垂直方向的分辨率。最后需要调用 win32api.ReleaseDC() 方法释放设备上下…...
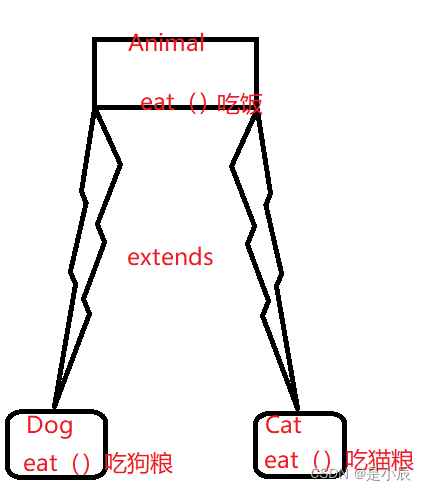
Java多态
目录 1.多态是什么? 2.多态的条件 3.重写 3.1重写的概念 3.2重写的作用 3.3重写的规则 4.向上转型与向下转型 4.1向上转型 4.2向下转型 5.多态的优缺点 5.1 优点 5.2 缺点 面向对象程序三大特性:封装、继承、多态。 1.多态是什么࿱…...

绝对路径和相对路径
1.绝对路径:从根目录为起点到某一个目录的路径 使用计算机时要找到需要的文件就必须知道文件的位置,表示文件的位置的方式就是路径,例如只要看到这个路径:c:/website/img/photo.jpg我们就知道photo.jpg文件是在c盘的website目录下…...

Linux第二次总结
Linux阶段总结 OSI模型:应用层、表示层、会话层、传输层、网络层、数据链路层、物理层 路由器的工作原理:最佳路径选择 三次握手四次挥手:... shell是翻译官把人类语言翻译成二进制语言 Tab作用:自动补齐、确认输入是否有误 …...
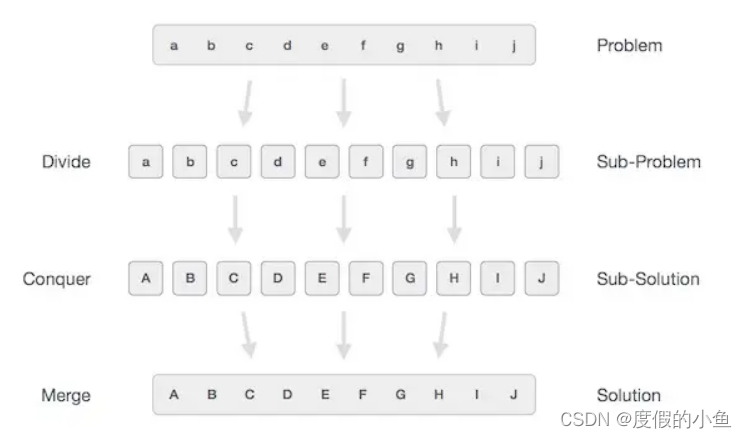
算法:贪婪算法、分而治之
算法:贪婪算法、分而治之 文章目录1.贪婪算法计数硬币实例12.分而治之分割/歇征服/解决合并/合并实例23.动态规划对照实例34.基本概念算法数据定义数据对象内置数据类型派生数据类型基本操作1.贪婪算法 设计算法以实现给定问题的最佳解决方案。在贪婪算法方法中&am…...

462. 最小操作次数使数组元素相等 II——【Leetcode每日一题】
462. 最小操作次数使数组元素相等 II 给你一个长度为 n 的整数数组 nums ,返回使所有数组元素相等需要的最小操作数。 在一次操作中,你可以使数组中的一个元素加 1 或者减 1 。 示例 1: 输入:nums [1,2,3] 输出:2 …...

对数据库的库及表的操作
全篇在MySQL操作下完成 在此之前,先介绍一下,字段、列类型及属性。 一、什么是字段、列类型、属性 (1)字段,一张表中列的名称;列类型,该列存储数据的类型;属性,描述列类型的特征。 …...

final类又没实现接口应该用哪一种代理, jdk动态代理还是cglib代理
jdk动态代理还是cglib代理🧙jdk动态代理和cglib代理的示例JDK动态代理原理CGLIB代理final类又没实现接口应该用哪一种代理, jdk动态代理还是cglib代理滚滚长江东逝水,浪花淘尽英雄。——唐代杨炯《临江仙》 jdk动态代理和cglib代理的示例 以下是一个使用…...

使用StaMPS_Visualizer
0 前言 StaMPS-Visualizer :由thho开发的用于可视化由StaMPS / MTI处理的DInSAR结果。 github地址:StaMPS-Visualizer 使用StaMPS_Visualizer需要配置好StaMPS,并安装好R和Rstudio Ubuntu中安装StaMPS StaMPS-Visualizer 安装步骤–在linux…...

高并发-高性能-高可用-结论版
文章目录上万的并发需要多少台web服务器一般单机能处理200请求,为何redis单机却能处理上万请求单线程每秒能处理(发送/响应)的http请求数三高的定义高并发的解决方案高性能的解决方案高可用的解决方案参考文章上万的并发需要多少台web服务器 …...

数智转型助力建筑业全产业链升级,你了解多少?
关于数智转型,指的是基于数字化技术和数据驱动的思维方式,将企业的管理、业务和服务进行全面的升级和改造,从而帮助实现企业的数字化转型和升级。通过数字技术和数据分析来提高企业的效率、创新能力和竞争力,进一步提高企业的市场…...
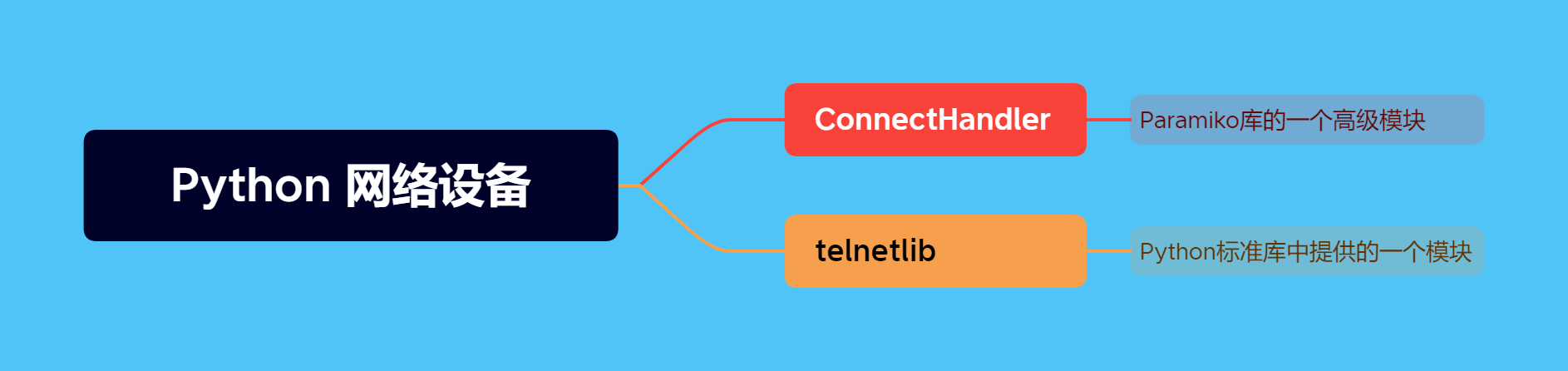
Python网络设备脚本中经常使用的connecthandler和telnetlib是什么意思?
你好,这里是网络技术联盟站。 在昨天的文章中,有小伙伴提到对这两天瑞哥提供的Python脚本中涉及的connecthandler和telnetlib两个模块不是太了解,想要学习一下: 今天瑞哥就安排上! 其实这两个模块是Python与网络设备…...

你真的会写 git commit message 吗?
作者:明明如月学长, CSDN 博客专家,蚂蚁集团高级 Java 工程师,《性能优化方法论》作者、《解锁大厂思维:剖析《阿里巴巴Java开发手册》》、《再学经典:《EffectiveJava》独家解析》专栏作者。 热门文章推荐…...
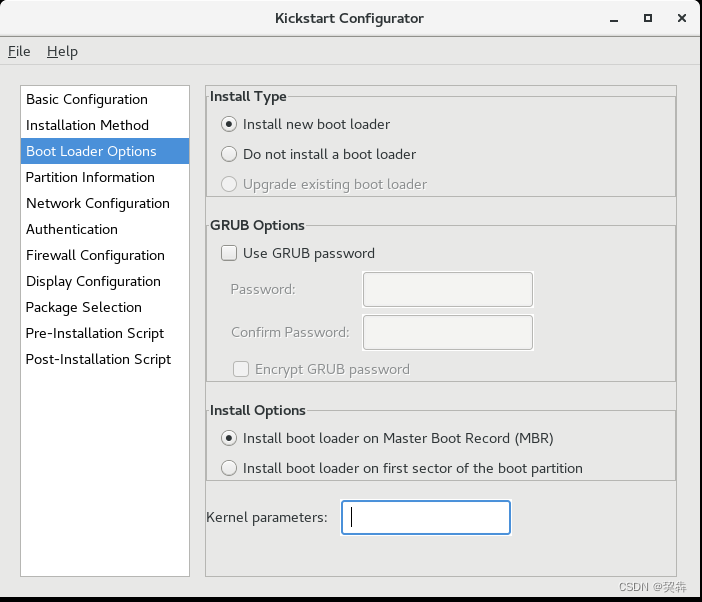
ISO文件内添加kickstart完成自动安装
目录 将待制作的centos iso文件挂载到/mnt/目录 将/mnt/下的所有文件复制到新的目录/tmp/mycentos 创建kickstart文件 修改启动文件 重新制作ISO文件 制作完成 kickstart可以实现根据配置自动安装操作系统,本文主要讲解如何让机器读取到iso文件后自动完成操作…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...
