算法:贪婪算法、分而治之
算法:贪婪算法、分而治之
文章目录
- 1.贪婪算法
- 计数硬币
- 实例1
- 2.分而治之
- 分割/歇
- 征服/解决
- 合并/合并
- 实例2
- 3.动态规划
- 对照
- 实例3
- 4.基本概念算法
- 数据定义
- 数据对象
- 内置数据类型
- 派生数据类型
- 基本操作
1.贪婪算法
设计算法以实现给定问题的最佳解决方案。在贪婪算法方法中,决策是从给定的解决方案域做出的。由于贪婪,选择了似乎提供最佳解决方案的最接近的解决方案。
贪心算法试图找到一个本地化的最优解决方案,最终可能导致全局优化的解决方案。但是,通常贪婪算法不提供全局优化的解决方案。
计数硬币
这个问题是通过选择最不可能的硬币来计算到期望的值,并且贪婪的方法迫使算法选择最大可能的硬币。如果我们提供₹1,2,5和10的硬币,我们被要求计算₹18,那么贪婪程序将是
- 1 - 选择一个₹10硬币,剩余计数为8
- 2 - 然后选择一个₹5硬币,剩余计数为3
- 3 - 然后选择一个₹2硬币,剩余计数为1
- 4 - 最后,选择一个₹1个硬币可以解决问题
虽然,它似乎工作正常,但这个数量我们只需要选择4个硬币。但是,如果我们稍微改变问题,那么相同的方法可能无法产生相同的最佳结果。
对于货币系统,我们有硬币值为1,7,10的值,计算值为18的硬币绝对是最佳的,但对于15的计数,它可能会使用超过必要的硬币。例如,贪婪的方法将使用10 + 1 + 1 + 1 + 1 + 1,总共6个硬币。而只使用3个硬币(7 + 7 + 1)就可以解决同样的问题
因此,我们可以得出结论,贪婪的方法选择了一个立即优化的解决方案,并且可能在全局优化成为主要问题的地方失败。
实例1
大多数网络算法都使用贪婪的方法。以下是其中一些列表 -
- 旅行推销员问题
- Prim的最小生成树算法
- Kruskal的最小生成树算法
- Dijkstra的最小生成树算法
- 图 - 地图着色
- 图 - 顶点覆盖
- 背包问题
- 作业调度问题
有许多类似的问题使用贪婪的方法来找到最佳解决方案。
2.分而治之
在分而治之的方法中,手头的问题被分成较小的子问题,然后每个问题都独立解决。当我们继续将子问题划分为更小的子问题时,我们最终可能会达到无法进行更多划分的阶段。解决那些“原子”最小可能的子问题(分数)。最后合并所有子问题的解决方案以获得原始问题的解决方案。
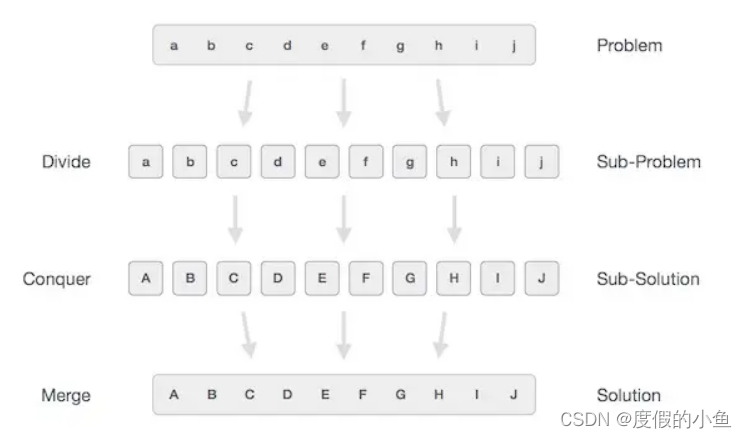
从广义上讲,我们可以通过三个步骤来理解 分而治之的 方法。
分割/歇
此步骤涉及将问题分解为更小的子问题。子问题应该代表原始问题的一部分。此步骤通常采用递归方法来划分问题,直到子问题不再可被整除为止。在这个阶段,子问题本质上是原子的,但仍然代表了实际问题的某些部分。
征服/解决
这一步收到了许多较小的子问题需要解决。通常,在这个层面上,问题被认为是自己“解决”的。
合并/合并
当解决较小的子问题时,该阶段递归地组合它们直到它们形成原始问题的解决方案。这种算法方法递归地工作并且征服和合并步骤的工作如此接近以至于它们看起来像一个。
实例2
以下计算机算法基于 分而治之的 编程方法 -
- 合并排序
- 快速排序
- 二进制搜索
- Strassen的矩阵乘法
- 最近的一对(点)
有多种方法可以解决任何计算机问题,但所提到的是分而治之的方法的一个很好的例子。
3.动态规划
动态编程方法类似于将问题分解为更小但更小的子问题的分而治之。但不同的是,分而治之,这些子问题并没有独立解决。相反,记住这些较小子问题的结果并用于类似或重叠的子问题。
动态编程用于我们遇到问题的地方,可以将其划分为类似的子问题,以便可以重复使用它们的结果。大多数情况下,这些算法用于优化。在解决现有子问题之前,动态算法将尝试检查先前解决的子问题的结果。结合子问题的解决方案以实现最佳解决方案。
所以我们可以说 -
- 该问题应该能够分成较小的重叠子问题。
- 通过使用较小子问题的最佳解决方案可以实现最佳解决方案。
- 动态算法使用Memoization。
对照
与解决局部优化的贪婪算法相反,动态算法被激励用于问题的整体优化。
与分而治之的算法相比,其中解决方案被组合以实现整体解决方案,动态算法使用较小子问题的输出,然后尝试优化更大的子问题。动态算法使用Memoization来记住已经解决的子问题的输出。
实例3
使用动态编程方法可以解决以下计算机问题 -
- 斐波纳契数系列
- 背包问题
- 河内塔
- 由Floyd-Warshall完成的所有最短路径
- Dijkstra的最短路径
- 项目安排
动态编程可以自上而下和自下而上的方式使用。当然,大多数情况下,参考之前的解决方案输出比CPU周期重新计算更便宜。
4.基本概念算法
本章介绍与数据结构相关的基本术语。
数据定义
数据定义定义具有以下特征的特定数据。
- 原子 - 定义应该定义一个单一的概念。
- 可追踪 - 定义应该能够映射到某些数据元素。
- 准确 - 定义应该是明确的。
- 清晰简洁 - 定义应该是可以理解的。
数据对象
数据对象表示具有数据的对象。
数据类型
数据类型是对诸如整数,字符串等各种类型的数据进行分类的一种方式,其确定可以与相应类型的数据一起使用的值,可以对相应类型的数据执行的操作的类型。有两种数据类型
- 内置数据类型
- 派生数据类型
内置数据类型
语言具有内置支持的那些数据类型称为内置数据类型。例如,大多数语言提供以下内置数据类型。
- 整型
- 布尔值(true,false)
- 浮动(十进制数)
- 人物和弦乐
派生数据类型
那些可以以一种或另一种方式实现的独立于实现的数据类型称为派生数据类型。这些数据类型通常由主数据类型或内置数据类型以及相关操作的组合构建。例如 -
- 名单
- 排列
- 堆
- 队列
基本操作
数据结构中的数据由某些操作处理。所选择的特定数据结构很大程度上取决于需要对数据结构执行的操作的频率。
- 遍历
- 搜索
- 插入
- 删除
- 排序
- 合并
相关文章:

算法:贪婪算法、分而治之
算法:贪婪算法、分而治之 文章目录1.贪婪算法计数硬币实例12.分而治之分割/歇征服/解决合并/合并实例23.动态规划对照实例34.基本概念算法数据定义数据对象内置数据类型派生数据类型基本操作1.贪婪算法 设计算法以实现给定问题的最佳解决方案。在贪婪算法方法中&am…...

462. 最小操作次数使数组元素相等 II——【Leetcode每日一题】
462. 最小操作次数使数组元素相等 II 给你一个长度为 n 的整数数组 nums ,返回使所有数组元素相等需要的最小操作数。 在一次操作中,你可以使数组中的一个元素加 1 或者减 1 。 示例 1: 输入:nums [1,2,3] 输出:2 …...

对数据库的库及表的操作
全篇在MySQL操作下完成 在此之前,先介绍一下,字段、列类型及属性。 一、什么是字段、列类型、属性 (1)字段,一张表中列的名称;列类型,该列存储数据的类型;属性,描述列类型的特征。 …...

final类又没实现接口应该用哪一种代理, jdk动态代理还是cglib代理
jdk动态代理还是cglib代理🧙jdk动态代理和cglib代理的示例JDK动态代理原理CGLIB代理final类又没实现接口应该用哪一种代理, jdk动态代理还是cglib代理滚滚长江东逝水,浪花淘尽英雄。——唐代杨炯《临江仙》 jdk动态代理和cglib代理的示例 以下是一个使用…...

使用StaMPS_Visualizer
0 前言 StaMPS-Visualizer :由thho开发的用于可视化由StaMPS / MTI处理的DInSAR结果。 github地址:StaMPS-Visualizer 使用StaMPS_Visualizer需要配置好StaMPS,并安装好R和Rstudio Ubuntu中安装StaMPS StaMPS-Visualizer 安装步骤–在linux…...

高并发-高性能-高可用-结论版
文章目录上万的并发需要多少台web服务器一般单机能处理200请求,为何redis单机却能处理上万请求单线程每秒能处理(发送/响应)的http请求数三高的定义高并发的解决方案高性能的解决方案高可用的解决方案参考文章上万的并发需要多少台web服务器 …...

数智转型助力建筑业全产业链升级,你了解多少?
关于数智转型,指的是基于数字化技术和数据驱动的思维方式,将企业的管理、业务和服务进行全面的升级和改造,从而帮助实现企业的数字化转型和升级。通过数字技术和数据分析来提高企业的效率、创新能力和竞争力,进一步提高企业的市场…...
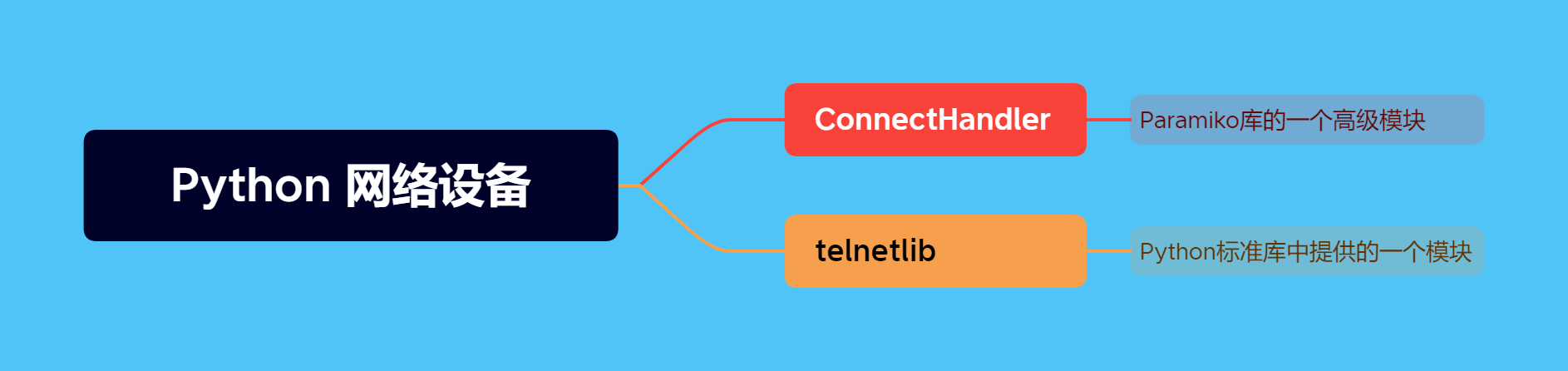
Python网络设备脚本中经常使用的connecthandler和telnetlib是什么意思?
你好,这里是网络技术联盟站。 在昨天的文章中,有小伙伴提到对这两天瑞哥提供的Python脚本中涉及的connecthandler和telnetlib两个模块不是太了解,想要学习一下: 今天瑞哥就安排上! 其实这两个模块是Python与网络设备…...

你真的会写 git commit message 吗?
作者:明明如月学长, CSDN 博客专家,蚂蚁集团高级 Java 工程师,《性能优化方法论》作者、《解锁大厂思维:剖析《阿里巴巴Java开发手册》》、《再学经典:《EffectiveJava》独家解析》专栏作者。 热门文章推荐…...
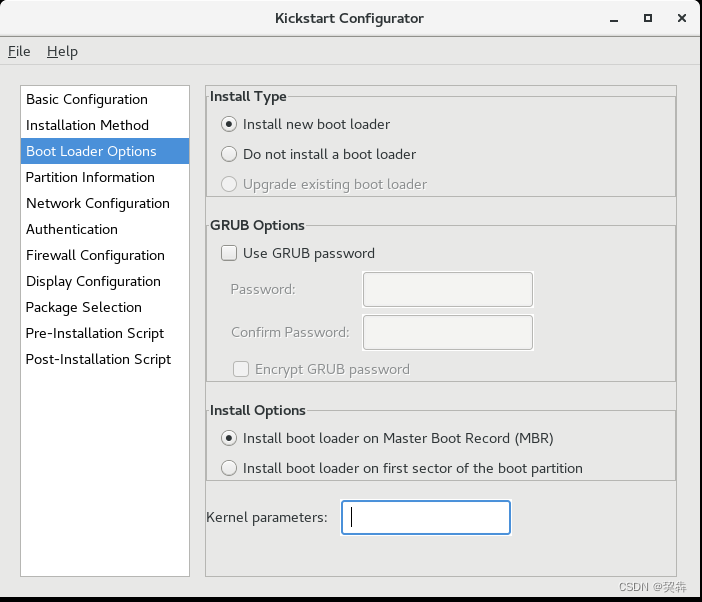
ISO文件内添加kickstart完成自动安装
目录 将待制作的centos iso文件挂载到/mnt/目录 将/mnt/下的所有文件复制到新的目录/tmp/mycentos 创建kickstart文件 修改启动文件 重新制作ISO文件 制作完成 kickstart可以实现根据配置自动安装操作系统,本文主要讲解如何让机器读取到iso文件后自动完成操作…...

SpringBoot 整合RabbitMq 自定义消息监听容器来实现消息批量处理
SpringBoot 整合RabbitMq 自定义消息监听容器来实现消息批量处理前言添加依赖配置文件编写监听器创建SimpleRabbitListenerContainerFactory发送消息前言 RabbitMQ是一种常用的消息队列,Spring Boot对其进行了深度的整合,可以快速地实现消息的发送和接收…...

jquery基础之操作节点对象
jquery操作节点(元素)对象 捕获-DOM操作,获取内容,值 获取内容:1.text()获取元素的文本内容 2.html()获取元素的文档内容 …...

对于Java的深入理解及其特点--面试
前言 计算机语言千千万,每一种语言都有其自己的特点、擅长的领域。在学习了Java之后才对Java有了进一步的理解。 面试问一: 你是如何理解Java这门语言的? 这里我们应该从下面几个点去总结 1、Java语言具有的属性 2、他的特点在哪 Java语…...

Linux GPSD的使用
目录 1: GPSD 运行状态查看 2:停止GPSD 服务 3: GPSD运行输出(协议的识别) 4:开启的服务...
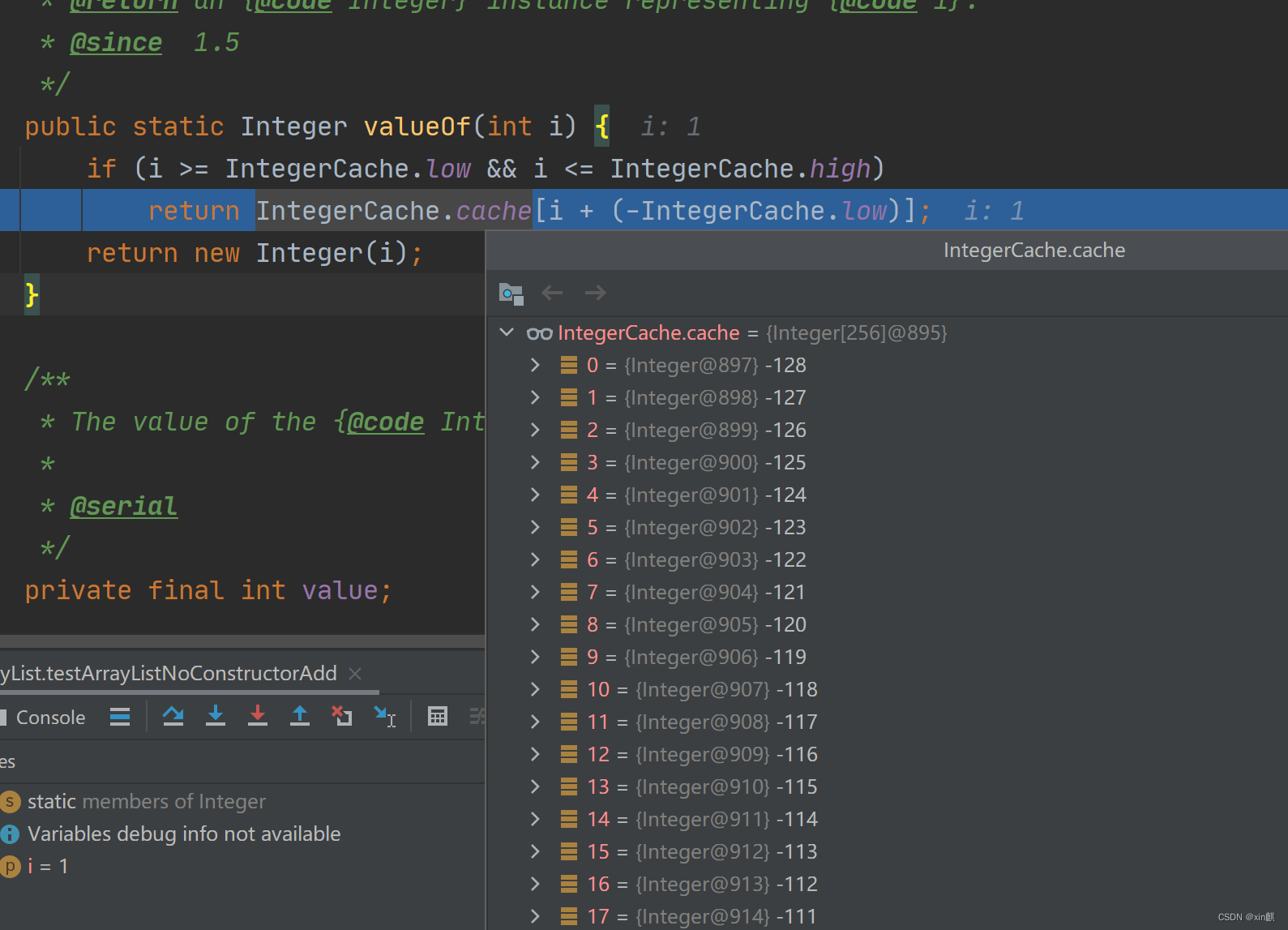
ArrayList无参构造添加元素源码解读
一、ArrayList无参构造add方法源码阅读 Test//无参构造源码阅读 public void testArrayListNoConstructorAdd(){ArrayList<Integer> arrayList new ArrayList<>();ArrayList<Integer> list new ArrayList<>();arrayList.add(1);arrayList.add(12);a…...
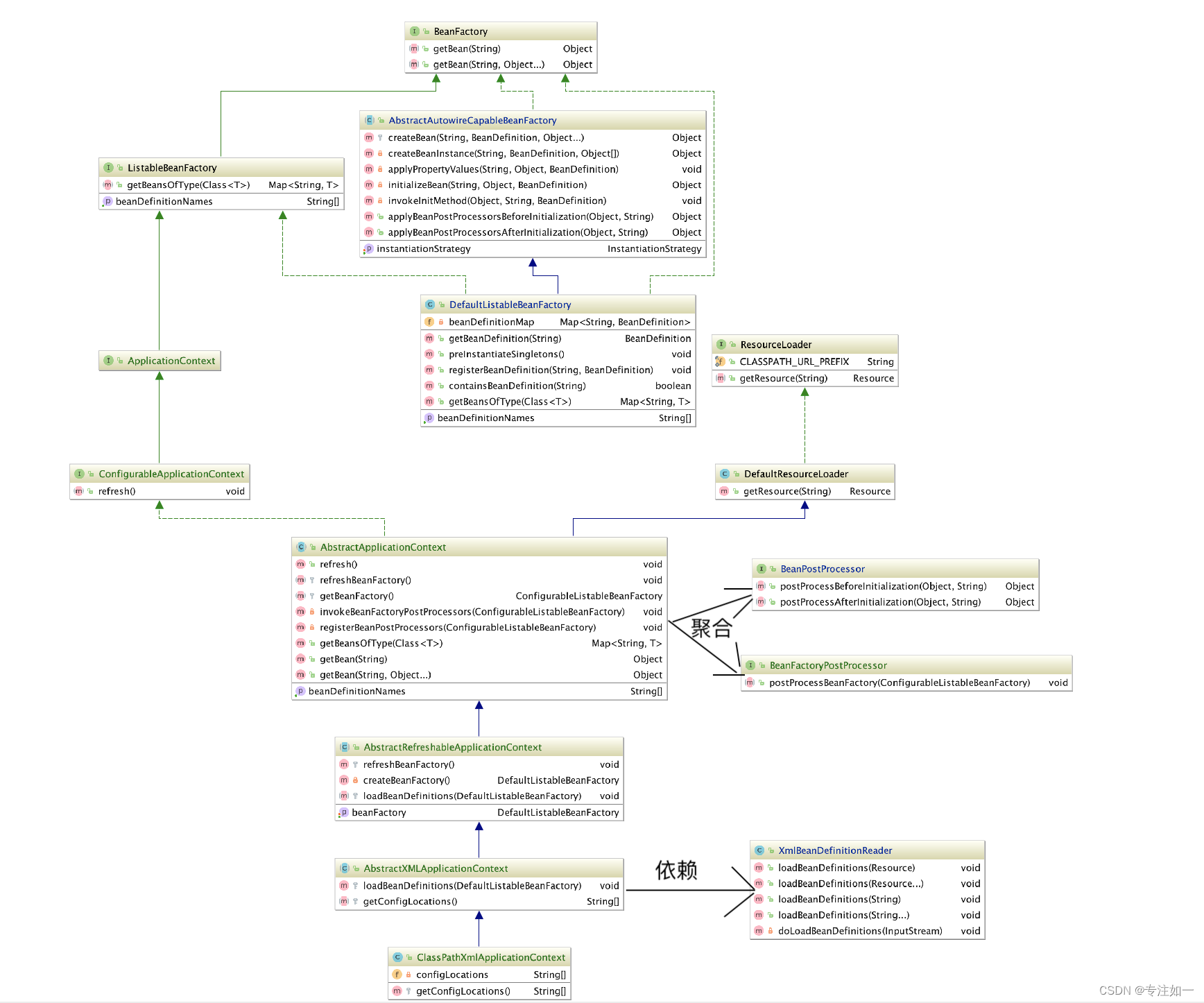
手写简易 Spring(二)
文章目录手写简易 Spring(二)1. 扩展 BeanFactory 接口2. 实现资源加载器,从 Spring.xml 解析和注册 Bean 对象1. 核心实现类 XmlBeanDefinitionReader3. 实现应用上下文,自动识别、资源加载、扩展机制1. 应用上下文2. 核心实现类…...

排列问题DFS入门
1、题目描述(全排列) 输入一个正整数n,输出1~n的全排列。 输入格式 一个正整数n。 输出格式 所有1~n的全排列,每个排列占一行。 样例输入 3 样例输出 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 算法思路 题目要求输出n的全…...

【每日一题Day159】LC1638统计只差一个字符的子串数目 | 枚举
统计只差一个字符的子串数目【LC1638】 给你两个字符串 s 和 t ,请你找出 s 中的非空子串的数目,这些子串满足替换 一个不同字符 以后,是 t 串的子串。换言之,请你找到 s 和 t 串中 恰好 只有一个字符不同的子字符串对的数目。 比…...

【07 Metadata and VendorTag】
1. Metadata结构及分类 一个 metadata 通过tag,value及 type 来描述。不同的 metadata 分成三类 controls,dynamic 及 static 2. MTK Metadata IMetadata Mtk metadata containerIMetadataConverter Provide mutual conversion for Android camera_metadata and MTK Imetada…...

Golang中Model的使用
导语我们都知道在Golang中我们一般都是设置GOPATH目录,这个目录主要存放我们的第三方包,这个方式一直不是很方便,今天给大家介绍Go 1.11版本中推出的GoModul使用方法,学过java的同学,可能对maven包有所了解,…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
