二叉搜索树 (BST) 节点插入、查找、删除、获取最大值、最小值和中序遍历排序等功能
二叉搜索树 (BST) 实现总结
本程序实现了一个简单的二叉搜索树 (BST),支持节点插入、查找、删除、获取最大值、最小值和中序遍历排序等功能。以下是各部分的详细说明。
数据结构
节点定义
struct BinTreeNode {int data; // 节点存储的数据struct BinTreeNode* left; // 指向左子节点的指针struct BinTreeNode* right; // 指向右子节点的指针
};函数定义
插入函数
void insert(BinTreeNode* &t, int x);- 功能: 将新值
x插入到二叉搜索树中。 - 逻辑:
-
- 如果当前节点
t为NULL,则创建新节点并赋值。 - 否则根据
x与t->data的比较,递归地决定插入左子树或右子树。
- 如果当前节点
查找最小值和最大值
int Min(BinTreeNode* bst);
int Max(BinTreeNode* bst);- 功能: 返回二叉搜索树中最小值和最大值。
- 逻辑:
-
- 最小值通过一直遍历左子树获取。
- 最大值通过一直遍历右子树获取。
中序遍历排序
void sort(BinTreeNode* t);- 功能: 打印二叉搜索树的节点值,按升序排列。
- 逻辑:
-
- 递归访问左子树,打印当前节点,再递归访问右子树。
查询 BST
BinTreeNode* searchBST(BinTreeNode* t, int key);- 功能: 查询树中是否存在值为
key的节点。 - 逻辑:
-
- 根据
key的值与当前节点的比较,决定递归访问左子树或右子树。
- 根据
删除节点
bool removeBST(BinTreeNode* t, int x);- 功能: 删除值为
x的节点。 - 逻辑:
-
- 递归查找节点
t。 - 一旦找到,判断其子节点情况并处理:
- 递归查找节点
-
-
- 叶子节点: 直接释放。
- 单子节点: 将当前节点替换为其唯一的子节点并释放。
- 双子节点: 找到左子树的最大值,替换当前节点数据,并删除该最大节点。
-
主函数
int main() {int ar[] = {53, 17, 78, 9, 45, 65, 87, 23};int n = sizeof(ar) / sizeof(ar[0]);BinTreeNode* bst = NULL;for (int i = 0; i < n; i++) {insert(bst, ar[i]); // 插入数组中的每个元素}removeBST(bst, 53); // 删除值为 53 的节点return 0;
}- 功能: 创建一个二叉搜索树并插入一组数据,然后删除指定节点。
- 逻辑:
-
- 使用数组
ar初始化树,插入每个元素。 - 调用
removeBST删除值为 53 的节点。
- 使用数组
可视化编译器
可视化编辑器 数据结构与算法 | 图码
相关文章:
 节点插入、查找、删除、获取最大值、最小值和中序遍历排序等功能)
二叉搜索树 (BST) 节点插入、查找、删除、获取最大值、最小值和中序遍历排序等功能
二叉搜索树 (BST) 实现总结 本程序实现了一个简单的二叉搜索树 (BST),支持节点插入、查找、删除、获取最大值、最小值和中序遍历排序等功能。以下是各部分的详细说明。 数据结构 节点定义 struct BinTreeNode {int data; // 节点存储的数…...

unity ps 2d animation 蛇的制作
一、PS的使用 1.打开PS 利用钢笔工具从下往上勾勒填充 2.复制图层,Ctrl T,w调为-100% 3.对齐图层并继续用钢笔工具进行三角勾勒 3.画眼睛,按U快捷键打开椭圆工具,按住Shift可以画圆,填充并复制图层对称。 4.画笔工具,打开小…...

39 C 语言枚举类型、枚举常量、枚举变量、枚举的遍历、枚举数组、枚举与 switch
目录 1 什么是枚举 2 定义枚举类型 2.1 语法格式 2.2 枚举元素的特点 2.3 案例演示 3 枚举变量 3.1 什么是枚举变量 3.2 定义枚举变量的多种方式 3.3 案例演示 1:标准版枚举类型 3.4 案例演示 2:简化版枚举类型 3.5 案例演示 3:匿…...

LabVIEW程序怎么解决 Bug?
在LabVIEW开发过程中,发现和解决程序中的Bug是确保系统稳定运行的关键环节。由于LabVIEW采用图形化编程方式,Bug的排查和处理与传统编程语言略有不同。以下是解决LabVIEW程序中Bug的常见方法和技巧,涵盖从问题发现到解决的多个步骤和角度&…...

AR智能眼镜之战:Meta vs Snap
随着增强现实(AR)技术的发展,各大科技公司都在争夺下一代计算平台的领先地位。Meta(前身为Facebook)和Snap作为其中的两个重要玩家,正在竞相开发能够提供沉浸式体验的AR智能眼镜。在这篇文章中,我们将深入探讨这两家公司可能采用的显示技术和用户体验,并分析它们各自的…...

Spring Boot 集成 Flowable UI 实现请假流程 Demo
博客主页: 南来_北往 系列专栏:Spring Boot实战 在现代企业应用中,工作流管理是一个至关重要的部分。通过使用Spring Boot和Flowable,可以方便地构建和管理工作流。本文将详细介绍如何在Spring Boot项目中集成Flowable UI,…...

毕业设计选题:基于ssm+vue+uniapp的医院管理系统小程序
开发语言:Java框架:ssmuniappJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:M…...

自动驾驶系列—线控悬架技术:自动驾驶背后的动力学掌控者
🌟🌟 欢迎来到我的技术小筑,一个专为技术探索者打造的交流空间。在这里,我们不仅分享代码的智慧,还探讨技术的深度与广度。无论您是资深开发者还是技术新手,这里都有一片属于您的天空。让我们在知识的海洋中…...
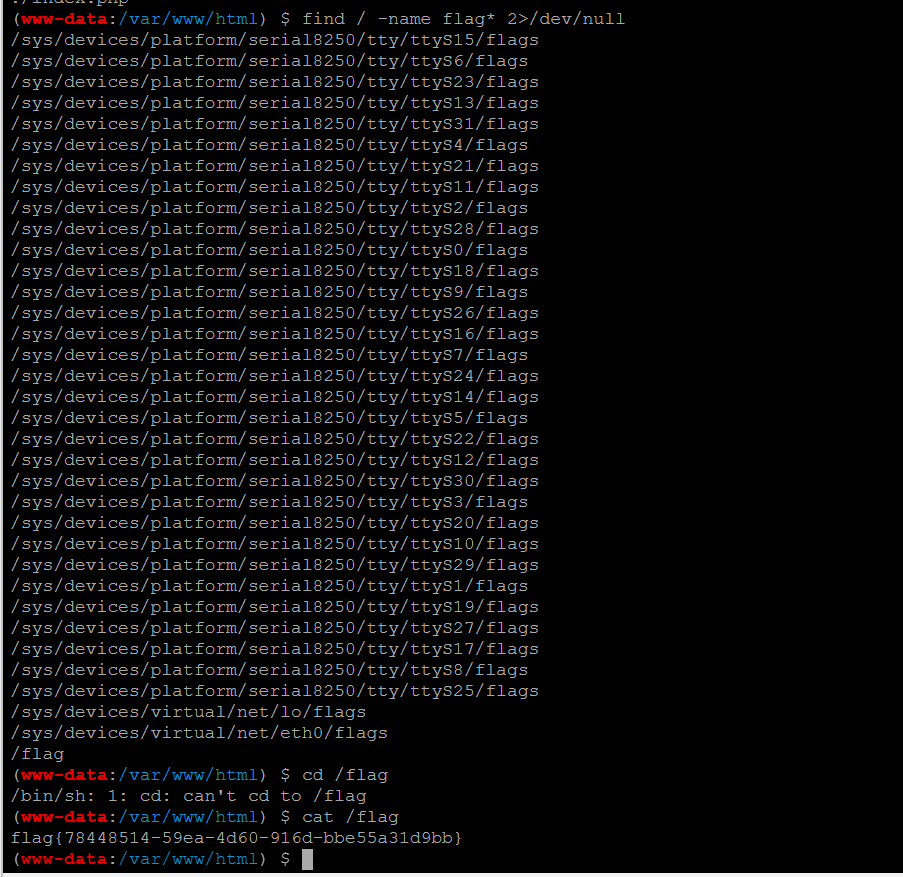
CTF刷题buuctf
[WUSTCTF2020]颜值成绩查询 拿到相关题目,其实根据功能和参数分析。需要传入一个学号然后进行针对于对应的学号进行一个查询,很可能就会存在sql注入。 其实这道题最难的点,在于过滤了空格,因此我们使用 /**/来过滤空格的限制。…...

Qt QWidget控件
目录 一、概述 二、Qwidget常用属性及函数介绍 2.1 enable 2.2 geometry 2.3 windowTitle 2.4 windowIcon 2.5 cursor 2.6 font 设置字体样式 2.7 toolTip 2.8 focusPolicy焦点策略 2.9 styleSheet 一、概述 widget翻译而来就是小控件,小部件。…...

如何通过Dockfile更改docker中ubuntu的apt源
首先明确我们有一个宿主机和一个docker环境,接下来的步骤是基于他们两个完成的 1.在宿主机上创建Dockerfile 随便将后面创建的Dockerfile放在一个位置,我这里选择的是 /Desktop 使用vim前默认你已经安装好了vim 2.在输入命令“vim Dockerfile”之后,…...

[C++][第三方库][jsoncpp]详细讲解
目录 1.介绍2.jsoncpp3.使用1.main.cc2.序列化3.反序列化 1.介绍 json是一种数据交换格式,采用完全独立于编程语言的文本格式来存储和表示数据json数据类型:对象、数组、字符串、数字 对象:使用{}括起来的表示一个对象数组:使用[…...

JavaScript中decodeURIComponent函数的深入解析与应用指南
在Web开发中,经常需要对URI(统一资源标识符)进行编码和解码,以保证数据传输的准确性和可靠性。decodeURIComponent函数是JavaScript中用于解码由encodeURIComponent函数或其他类似方法编码的部分统一资源标识符(URI&am…...

DMA方式为什么无需保护现场
DMA(Direct Memory Access)方式无需保护现场的原因主要与其工作原理和硬件设计有关。以下是对这一问题的详细解释: DMA工作原理 DMA是一种通过硬件直接在内存和外设之间传输数据的技术,无需CPU的介入。在DMA传输过程中ÿ…...

区块链可投会议CCF C--FC 2025 截止10.8 附录用率
Conference:Financial Cryptography and Data Security (FC) CCF level:CCF C Categories:network and information security Year:2025 Conference time:14–18 April 2025, Miyakojima, Japan 录用率࿱…...

springboot系列--web相关知识探索四
一、前言 web相关知识探索三中研究了请求中所带的参数是如何映射到接口参数中的,也即请求参数如何与接口参数绑定。主要有四种、分别是注解方式、Servlet API方式、复杂参数、以及自定义对象参数。web相关知识探索三中主要研究了注解方式以及Servlet API方式。本次…...

在PyQt5中,清空一个QFrame中的所有控件
在PyQt5中,如果你想要清空一个QFrame中的所有控件,你需要遍历该QFrame的布局(假设你已经在其中添加了一个布局,比如QVBoxLayout或QHBoxLayout),并从布局中移除所有的控件。由于直接从布局中移除控件并不会立…...

SpringBoot实现:校园资料分享平台开发指南
1系统概述 1.1 研究背景 如今互联网高速发展,网络遍布全球,通过互联网发布的消息能快而方便的传播到世界每个角落,并且互联网上能传播的信息也很广,比如文字、图片、声音、视频等。从而,这种种好处使得互联网成了信息传…...
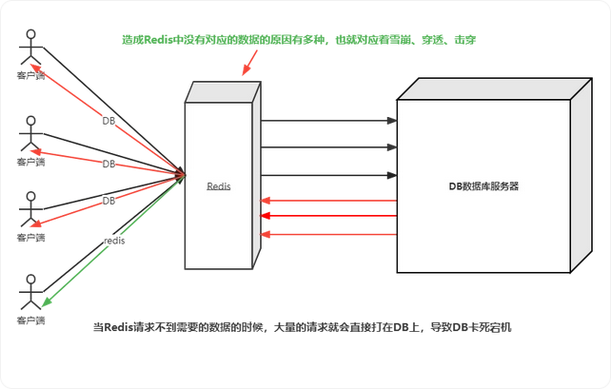
Redis篇(缓存机制 - 基本介绍)(持续更新迭代)
目录 一、缓存介绍 二、经典三缓存问题 1. 缓存穿透 1.1. 简介 1.2. 解决方案 1.3. 总结 2. 缓存雪崩 2.1. 简介 2.2. 解决方案 2.3. 总结 3. 缓存击穿 3.1. 简介 3.2. 解决方案 3.3. 总结 4. 经典三缓存问题出现的根本原因 三、常见双缓存方案 1. 缓存预热 1…...

引领5G驱动的全球数字营销革新:章鱼移动广告全球平台的崛起
引领5G驱动的全球数字营销革新:章鱼移动广告全球平台的崛起 作为章鱼移动广告平台的营销战略顾问,黄珍珍通过她在市场营销、品牌推广、技术整合等多方面的丰富经验,成功推动了这一平台在全球广告市场的崛起。她不仅为平台的国际化扩展奠定了基…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
