正态分布的极大似然估计一个示例,详细展开的方程求解步骤
此示例是 什么是极大似然估计 中的一个例子,本文的目的是给出更加详细的方程求解步骤,便于数学基础不好的同学理解。
目标
假设我们有一组样本数据 x 1 , x 2 , … , x n x_1, x_2, \dots, x_n x1,x2,…,xn,它们来自一个正态分布 N ( μ , σ 2 ) N(\mu, \sigma^2) N(μ,σ2),我们的目标是通过极大似然估计(MLE)来找到正态分布的两个参数 μ \mu μ 和 σ 2 \sigma^2 σ2。
对数似然函数
正态分布的概率密度函数为:
f ( x i ∣ μ , σ 2 ) = 1 2 π σ 2 exp ( − ( x i − μ ) 2 2 σ 2 ) f(x_i | \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left( -\frac{(x_i - \mu)^2}{2\sigma^2} \right) f(xi∣μ,σ2)=2πσ21exp(−2σ2(xi−μ)2)
给定样本 x 1 , x 2 , … , x n x_1, x_2, \dots, x_n x1,x2,…,xn,样本的似然函数为:
L ( μ , σ 2 ) = ∏ i = 1 n 1 2 π σ 2 exp ( − ( x i − μ ) 2 2 σ 2 ) L(\mu, \sigma^2) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left( -\frac{(x_i - \mu)^2}{2\sigma^2} \right) L(μ,σ2)=i=1∏n2πσ21exp(−2σ2(xi−μ)2)
对似然函数取对数,得到对数似然函数:
ℓ ( μ , σ 2 ) = log L ( μ , σ 2 ) = ∑ i = 1 n log ( 1 2 π σ 2 exp ( − ( x i − μ ) 2 2 σ 2 ) ) \ell(\mu, \sigma^2) = \log L(\mu, \sigma^2) = \sum_{i=1}^n \log \left( \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left( -\frac{(x_i - \mu)^2}{2\sigma^2} \right) \right) ℓ(μ,σ2)=logL(μ,σ2)=i=1∑nlog(2πσ21exp(−2σ2(xi−μ)2))
我们可以将对数似然函数分解为三部分:
ℓ ( μ , σ 2 ) = − n 2 log ( 2 π ) − n 2 log ( σ 2 ) − 1 2 σ 2 ∑ i = 1 n ( x i − μ ) 2 \ell(\mu, \sigma^2) = -\frac{n}{2} \log(2\pi) - \frac{n}{2} \log(\sigma^2) - \frac{1}{2\sigma^2} \sum_{i=1}^n (x_i - \mu)^2 ℓ(μ,σ2)=−2nlog(2π)−2nlog(σ2)−2σ21i=1∑n(xi−μ)2
现在我们分别对 μ \mu μ 和 σ 2 \sigma^2 σ2 求导。
一、对 μ \mu μ 求导
首先,对 μ \mu μ 求导,方程中的 μ \mu μ 仅出现在最后一项 ∑ i = 1 n ( x i − μ ) 2 \sum_{i=1}^n (x_i - \mu)^2 ∑i=1n(xi−μ)2 中,因此我们只对这一项求导:
ℓ ( μ , σ 2 ) = − 1 2 σ 2 ∑ i = 1 n ( x i − μ ) 2 \ell(\mu, \sigma^2) = -\frac{1}{2\sigma^2} \sum_{i=1}^n (x_i - \mu)^2 ℓ(μ,σ2)=−2σ21i=1∑n(xi−μ)2
对 μ \mu μ 求导:
∂ ℓ ∂ μ = − 1 2 σ 2 ⋅ 2 ∑ i = 1 n ( x i − μ ) ( − 1 ) \frac{\partial \ell}{\partial \mu} = -\frac{1}{2\sigma^2} \cdot 2 \sum_{i=1}^n (x_i - \mu) (-1) ∂μ∂ℓ=−2σ21⋅2i=1∑n(xi−μ)(−1)
简化后为:
∂ ℓ ∂ μ = 1 σ 2 ∑ i = 1 n ( x i − μ ) \frac{\partial \ell}{\partial \mu} = \frac{1}{\sigma^2} \sum_{i=1}^n (x_i - \mu) ∂μ∂ℓ=σ21i=1∑n(xi−μ)
将这个导数设为 0,来找到 μ \mu μ 的极大似然估计:
1 σ 2 ∑ i = 1 n ( x i − μ ) = 0 \frac{1}{\sigma^2} \sum_{i=1}^n (x_i - \mu) = 0 σ21i=1∑n(xi−μ)=0
因为 σ 2 ≠ 0 \sigma^2 \neq 0 σ2=0,我们可以省略 1 σ 2 \frac{1}{\sigma^2} σ21,得到:
∑ i = 1 n ( x i − μ ) = 0 \sum_{i=1}^n (x_i - \mu) = 0 i=1∑n(xi−μ)=0
简化为:
n μ = ∑ i = 1 n x i n\mu = \sum_{i=1}^n x_i nμ=i=1∑nxi
因此, μ \mu μ 的极大似然估计为:
μ ^ = 1 n ∑ i = 1 n x i \hat{\mu} = \frac{1}{n} \sum_{i=1}^n x_i μ^=n1i=1∑nxi
这意味着,样本的均值是 μ \mu μ 的极大似然估计。
二、对 σ 2 \sigma^2 σ2 求导
接下来我们对 σ 2 \sigma^2 σ2 求导。对数似然函数中关于 σ 2 \sigma^2 σ2 的部分是:
ℓ ( μ , σ 2 ) = − n 2 log ( 2 π ) − n 2 log ( σ 2 ) − 1 2 σ 2 ∑ i = 1 n ( x i − μ ) 2 \ell(\mu, \sigma^2) = -\frac{n}{2} \log(2\pi) - \frac{n}{2} \log(\sigma^2) - \frac{1}{2\sigma^2} \sum_{i=1}^n (x_i - \mu)^2 ℓ(μ,σ2)=−2nlog(2π)−2nlog(σ2)−2σ21i=1∑n(xi−μ)2
我们对 σ 2 \sigma^2 σ2 求导,逐项进行求导:
-
第一项 − n 2 log ( 2 π ) -\frac{n}{2} \log(2\pi) −2nlog(2π) 是常数,对 σ 2 \sigma^2 σ2 求导为 0。
-
第二项 − n 2 log ( σ 2 ) -\frac{n}{2} \log(\sigma^2) −2nlog(σ2):
使用对数函数的求导公式 d d σ 2 ( log σ 2 ) = 1 σ 2 \frac{d}{d\sigma^2} (\log \sigma^2) = \frac{1}{\sigma^2} dσ2d(logσ2)=σ21,我们有:
∂ ∂ σ 2 ( − n 2 log ( σ 2 ) ) = − n 2 σ 2 \frac{\partial}{\partial \sigma^2} \left( -\frac{n}{2} \log(\sigma^2) \right) = -\frac{n}{2\sigma^2} ∂σ2∂(−2nlog(σ2))=−2σ2n -
第三项 − 1 2 σ 2 ∑ i = 1 n ( x i − μ ) 2 -\frac{1}{2\sigma^2} \sum_{i=1}^n (x_i - \mu)^2 −2σ21∑i=1n(xi−μ)2:
使用 d d σ 2 ( 1 σ 2 ) = − 1 σ 4 \frac{d}{d\sigma^2} \left( \frac{1}{\sigma^2} \right) = -\frac{1}{\sigma^4} dσ2d(σ21)=−σ41,我们得到:
∂ ∂ σ 2 ( − 1 2 σ 2 ∑ i = 1 n ( x i − μ ) 2 ) = 1 2 σ 4 ∑ i = 1 n ( x i − μ ) 2 \frac{\partial}{\partial \sigma^2} \left( - \frac{1}{2\sigma^2} \sum_{i=1}^n (x_i - \mu)^2 \right) = \frac{1}{2\sigma^4} \sum_{i=1}^n (x_i - \mu)^2 ∂σ2∂(−2σ21i=1∑n(xi−μ)2)=2σ41i=1∑n(xi−μ)2
将各项导数结果组合
我们将对数似然函数中所有关于 σ 2 \sigma^2 σ2 的项求导结果组合起来:
∂ ℓ ∂ σ 2 = − n 2 σ 2 + 1 2 σ 4 ∑ i = 1 n ( x i − μ ) 2 \frac{\partial \ell}{\partial \sigma^2} = -\frac{n}{2\sigma^2} + \frac{1}{2\sigma^4} \sum_{i=1}^n (x_i - \mu)^2 ∂σ2∂ℓ=−2σ2n+2σ41i=1∑n(xi−μ)2
设置导数为 0,解出 σ 2 \sigma^2 σ2
为了找到 σ 2 \sigma^2 σ2 的极大似然估计,我们将导数设为 0:
− n 2 σ 2 + 1 2 σ 4 ∑ i = 1 n ( x i − μ ) 2 = 0 -\frac{n}{2\sigma^2} + \frac{1}{2\sigma^4} \sum_{i=1}^n (x_i - \mu)^2 = 0 −2σ2n+2σ41i=1∑n(xi−μ)2=0
1. 消去常数 1 2 \frac{1}{2} 21
为了简化方程,两边同时乘以 2 消去常数:
− n σ 2 + 1 σ 4 ∑ i = 1 n ( x i − μ ) 2 = 0 -\frac{n}{\sigma^2} + \frac{1}{\sigma^4} \sum_{i=1}^n (x_i - \mu)^2 = 0 −σ2n+σ41i=1∑n(xi−μ)2=0
2. 将 n σ 2 \frac{n}{\sigma^2} σ2n 移到右边
将方程重排:
1 σ 4 ∑ i = 1 n ( x i − μ ) 2 = n σ 2 \frac{1}{\sigma^4} \sum_{i=1}^n (x_i - \mu)^2 = \frac{n}{\sigma^2} σ41i=1∑n(xi−μ)2=σ2n
3. 乘以 σ 4 \sigma^4 σ4
为了消去 σ 4 \sigma^4 σ4,我们将方程两边乘以 σ 4 \sigma^4 σ4:
∑ i = 1 n ( x i − μ ) 2 = n σ 2 \sum_{i=1}^n (x_i - \mu)^2 = n \sigma^2 i=1∑n(xi−μ)2=nσ2
4. 解出 σ 2 \sigma^2 σ2
将 σ 2 \sigma^2 σ2 留在一边,解出:
σ 2 = 1 n ∑ i = 1 n ( x i − μ ) 2 \sigma^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \mu)^2 σ2=n1i=1∑n(xi−μ)2
这个结果就是 σ 2 \sigma^2 σ2 的极大似然估计,即样本方差公式。
总结
我们通过对正态分布的对数似然函数分别对 μ \mu μ 和 σ 2 \sigma^2 σ2 求导,得到以下结论:
-
均值 μ \mu μ 的极大似然估计:
μ ^ = 1 n ∑ i = 1 n x i \hat{\mu} = \frac{1}{n} \sum_{i=1}^n x_i μ^=n1i=1∑nxi
即样本的均值是 μ \mu μ 的极大似然估计。 -
方差 σ 2 \sigma^2 σ2 的极大似然估计:
σ ^ 2 = 1 n ∑ i = 1 n ( x i − μ ^ ) 2 \hat{\sigma}^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \hat{\mu})^2 σ^2=n1i=1∑n(xi−μ^)2
即样本方差是 σ 2 \sigma^2 σ2 的极大似然估计。
相关文章:

正态分布的极大似然估计一个示例,详细展开的方程求解步骤
此示例是 什么是极大似然估计 中的一个例子,本文的目的是给出更加详细的方程求解步骤,便于数学基础不好的同学理解。 目标 假设我们有一组样本数据 x 1 , x 2 , … , x n x_1, x_2, \dots, x_n x1,x2,…,xn,它们来自一个正态分布 N…...

s7-200SMART编程软件下载
1、官网: STEP 7 Micro/WIN SMART V2.2 完整版http://w2.siemens.com.cn/download/smart/STEP%207%20MicroWIN%20SMART%20V2.2.zip STEP 7 Micro/WIN SMART V2.3 完整版http://w2.siemens.com.cn/download/smart/STEP%207%20MicroWIN%20SMART%20V2.3.iso STEP 7 Mi…...

Linux驱动开发常用调试方法汇总
引言:在 Linux 驱动开发中,调试是一个至关重要的环节。开发者需要了解多种调试方法,以便能够快速定位和解决问题。 1.利用printk 描述: printk 是 Linux 内核中的一个调试输出函数,类似于用户空间中的 printf。它用于…...

将列表中的各字符串sn连接成为一个字符串s使用;将各sn间隔开os.pathsep.join()
【小白从小学Python、C、Java】 【考研初试复试毕业设计】 【Python基础AI数据分析】 将列表中的各字符串sn 连接成为一个字符串s 使用;将各sn间隔开 os.pathsep.join() [太阳]选择题 下列说法中正确的是? import os paths ["/a", "/b/c", "/d&q…...
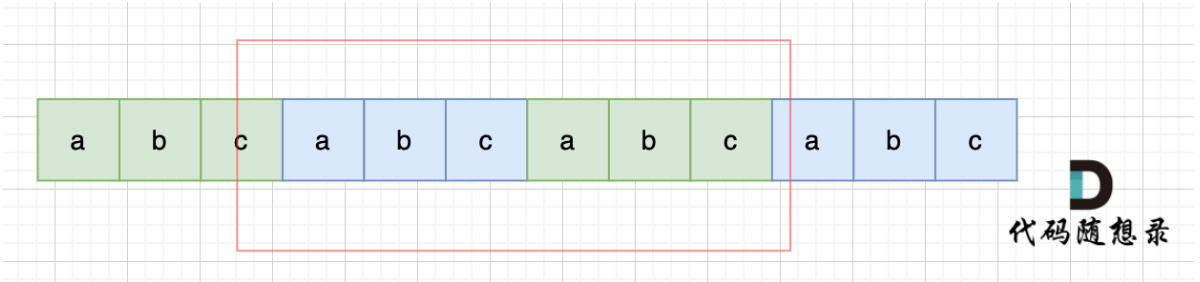
算法题总结(八)——字符串
531、反转字符串二 给定一个字符串 s 和一个整数 k,从字符串开头算起,每计数至 2k 个字符,就反转这 2k 字符中的前 k 个字符。 如果剩余字符少于 k 个,则将剩余字符全部反转。如果剩余字符小于 2k 但大于或等于 k 个,…...

大数据开发--1.2 Linux介绍及虚拟机网络配置
目录 一. 计算机入门知识介绍 软件和硬件的概述 硬件 软件 操作系统概述 简单介绍 常见的系统操作 学习Linux系统 二. Linux系统介绍 简单介绍 发行版介绍 常用的发行版 三. Linux系统的安装和体验 Linux系统的安装 介绍 虚拟机原理 常见的虚拟机软件 体验Li…...

2024CSP-J复赛易错点
低级错误 不开long long见祖宗写代码要有输入,别没写输入就交写完代码要在本地测试,多想写极端测试数据,或对拍注意考官说文件夹怎么建,别文件夹建错,爆0别忘写freopen或忘给freopen去注释记着把.exe文件删掉考试时不…...

pytorch 与 pytorch lightning, pytorch geometric 各个版本之间的关系
主要参考 官方的给出的意见; 1. pytorch 与 pytorch lightning 各个版本之间的关系 lightning 主要可以 适配多个版本的 torch; https://lightning.ai/docs/pytorch/latest/versioning.html#compatibility-matrix; 2. pytorch 与 pytorch geometric 各…...

Spring Boot项目的创建与使用
1.通过IDE创建Spring Boot项目 2.目录结构 3.新建TestController控制器 Controller public class TestController {RequestMapping("/test")public ModelAndView test(RequestParam(name "name", defaultValue "刘德华") String name){ModelA…...

pytorch常用函数view、sum、sequeeze、cat和chunk
文章目录 view()函数sequeeze和unsequeezecat和chunk函数sum函数view()函数 view()相当于reshape、resize,重新调整Tensor的形状。 指定调整形状之后的维度import torch re = torch.tensor([1, 2, 3, 4, 5...

【STM32开发之寄存器版】(四)-独立看门狗IWDG
一 、前言 独立看门狗简介: STM32F103ZET6内置两个看门狗,提供了更高的安全性、时间的精确性和使用的灵活性。两个看门狗设备(独立看门狗和窗口看门狗)可用来检测和解决由软件错误引起的故障。 独立看门狗主要性能: 自由运行的递减计数器时钟…...

【S32K3 RTD MCAL 篇1】 K344 KEY 控制 EMIOS PWM
【S32K3 RTD MCAL 篇1】 K344 KEY 控制 EMIOS PWM 一,文档简介二, 功能实现2.1 软硬件平台2.2 软件控制流程2.3 资源分配概览2.4 EB 配置2.4.1 Dio module2.4.2 Icu module2.4.4 Mcu module2.4.5 Platform module2.4.6 Port module2.4.7 Pwm module 2.5 …...
)
华为OD机试真题---绘图机器(计算面积)
题目描述 绘图机器的绘图笔初始位置在原点(0,0),机器启动后按照以下规则绘制直线: 尝试沿着横线坐标正向绘制直线直到给定的终点E。期间可以通过指令在纵坐标轴方向进行偏移,offsetY为正数表示正向偏移,为负数表示负向偏移。 给…...
HarmonyOs 查看官方文档使用弹窗
1. 学会查看官方文档 HarmonyOS跟上网上的视频学习一段时间后,基本也就入门了,但是有一些操作网上没有找到合适教学的视频,这时,大家就需要养成参考官方文档的习惯了,因为官方的开发文档是我们学习深度任何一门语言或…...

uniapp+Android智慧居家养老服务平台 0fjae微信小程序
目录 项目介绍支持以下技术栈:具体实现截图HBuilderXuniappmysql数据库与主流编程语言java类核心代码部分展示登录的业务流程的顺序是:数据库设计性能分析操作可行性技术可行性系统安全性数据完整性软件测试详细视频演示源码获取方式 项目介绍 老年人 登…...

在一台电脑上实现网页与exe程序使用udp通信
要在同一台电脑上实现网页(前端)与 EXE 程序(后端)通过 UDP 通信,可以使用以下步骤。前端可以使用 JavaScript 通过 WebSocket 与自定义服务器进行通信,该服务器通过 UDP 发送和接收数据,再与 E…...

基于Java的GeoTools对Shapefile文件属性信息深度解析
目录 前言 一、Shapefile的属性列表信息 1、属性表格信息 2、属性表格包含的要素 二、GeoTools对属性表格的解析 1、常规解析方法 2、基于dbf文件的属性信息读取 三、总结 前言 ESRI Shapefile(shp),或简称shapefile,是美…...

付费计量系统实体和接口(1)
13.System entities and interfaces 系统实体和接口 See also Clause 4 for a discussion on general concepts and Clause 5 for generic entity model. 参见条目 4 讨论总体概念、条目 5 通用实体模型。 An entity specification should specify the embodied functions and …...

网易博客旧文----bacnet学习系列之四----VTS的初步使用
bacnet学习系列之四----VTS的初步使用 2014-02-07 13:32:28| 分类: BACnet | 标签: |举报 |字号大中小 订阅 这是一个测试用 的工具,而且是开放源码的,下载地址为:VTS下载官网 也可以从我的网盘下载 VTS下载 我用的是…...

SpringIoC容器的初识
一、SpringIoC容器的介绍 Spring IoC 容器,负责实例化、配置和组装 bean(组件)。容器通过读取配置元数据来获取有关要实例化、配置和组装组件的指令。配置元数据以 XML、Java 注解或 Java 代码形式表现。它允许表达组成应用程序的组件以及这…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
