【动态规划-最长公共子序列(LCS)】【hard】【科大讯飞笔试最后一题】力扣115. 不同的子序列
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 10^9 + 7 取模。
示例 1:
输入:s = “rabbbit”, t = “rabbit”
输出:3
解释:
如下所示, 有 3 种可以从 s 中得到 “rabbit” 的方案。

示例 2:
输入:s = “babgbag”, t = “bag”
输出:5
解释:
如下所示, 有 5 种可以从 s 中得到 “bag” 的方案。

提示:
1 <= s.length, t.length <= 1000
s 和 t 由英文字母组成
动态规划
class Solution {
public:int numDistinct(string s, string t) {int MOD = 1e9 + 7;int m = s.size(), n = t.size();if(n > m){return 0;}vector<vector<int>> f(m+1, vector<int>(n+1));for(int i = 0; i <= m; i++){f[i][0] = 1;}for(int i = 1; i <= m; i++){for(int j = 1; j <= min(i, n) ; j++){if(s[i-1] == t[j-1]){f[i][j] = (f[i-1][j-1] + f[i-1][j]) % MOD;}else{f[i][j] = f[i-1][j] % MOD;}}}return f[m][n];}
};
时间复杂度:O(mn),其中 m 和 n 分别是字符串 s 和 t 的长度。二维数组 dp 有 m+1 行和 n+1 列,需要对 dp 中的每个元素进行计算。
空间复杂度:O(mn),其中 m 和 n 分别是字符串 s 和 t 的长度。创建了 m+1 行 n+1 列的二维数组 dp。
这个题运用了动态规划的思想,我们首先定义一个二维动态数组f[i][j],设 f[i][j] 表示字符串 s 的前 i 个字符中,子序列中 t 的前 j 个字符出现的次数。
如果 s[i - 1] == t[j - 1],那么 f[i][j] 既可以选择使用 s[i - 1] 来匹配 t[j - 1],也可以不使用 s[i - 1]。此时状态转移方程为:
f[i][j] = (f[i-1][j-1] + f[i-1][j]) % MOD;
如果 s[i - 1] != t[j - 1],则无法匹配 t[j - 1],因此只能继承之前的状态:
f[i][j] = f[i - 1][j]
最后返回f[m][n]。
优化:滚动数组
class Solution {
public:int numDistinct(string s, string t) {int MOD = 1e9 + 7;int m = s.size(), n = t.size();if(n > m){return 0;}vector<int> f(n+1);f[0] = 1;for(int i = 1; i <= m; i++){for(int j = min(i, n); j >= 1 ; j--){if(s[i-1] == t[j-1]){f[j] = (f[j-1] + f[j]) % MOD;}}}return f[n];}
};
我们可以观察到f[i][j] = (f[i-1][j-1] + f[i-1][j]) % MOD;中,f[I][j]上一行的前一个字符转换而来,还有由同一行的前一个字符转换而来。所以我们可以省去行的空间,只定义一个包含列的一维数组f[n],我们在循环中让j倒序,我们就有f[j-1]等同于f[i-1][j-1],f[j]等同于f[i-1][j]。并且在f[i][j] = f[i-1][j] % MOD;中,f[i-1][j]会转换成f[j] = f[j],所以我们不需要列出这种情况。
相关文章:

【动态规划-最长公共子序列(LCS)】【hard】【科大讯飞笔试最后一题】力扣115. 不同的子序列
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 10^9 7 取模。 示例 1: 输入:s “rabbbit”, t “rabbit” 输出:3 解释: 如下所示, 有 3 种可以从 s 中得到 “rabbit”…...

深入理解 JavaScript 中的 void`运算符和 yield*表达式
深入理解 JavaScript 中的 void 运算符和 yield* 表达式 在 JavaScript 中,void 运算符和 yield* 表达式是两个功能独特但常被忽视的运算符。本文将详细介绍它们的用法和应用场景,帮助您更好地理解和运用这两个运算符。 目录 void 运算符概述void 运算…...

第四节——从深层剖析指针(让你不再害怕指针)
文章目录 1. 字符指针变量剑指offer例题 2. 数组指针变量2.1 数组指针变量是什么?2.2 数组指针变量怎么初始化 3. ⼆维数组传参的本质代码实现 4. 函数指针变量4.1 函数指针变量的创建4.3 两段有趣的代码4.3.1 typedef 关键字 5. 函数指针数组的定义 1. 字符指针变量…...

openpnp - 吸嘴校正失败的opencv参数分析
文章目录 openpnp - 吸嘴校正失败的opencv参数分析概述笔记阶段验证 - N2吸嘴校验完NT1NT2 阶段验证 - 底部相机高级校验完NT1NT2 参数比对保存 “阶段验证 - N2吸嘴校验完” 的NT1/NT2图像重建参数检测环境NT1ok的3个参数值NT1err的3个参数值NT2ok的3个参数值NT2err的3个参数值…...

【Python】Marmir 使用指南:Python 驱动的电子表格生成器
Marmir 是一个由 Python 驱动的电子表格生成工具,专门用于将 Python 数据结构(如字典、列表等)转换为电子表格文件(如 Excel)。Marmir 的设计目标是提供比传统电子表格库(如 xlwt)更强大和灵活的…...

深入理解 JavaScript 事件循环机制:单线程中的异步处理核心
深入理解 JavaScript 事件循环机制:单线程中的异步处理核心 JavaScript 是一门单线程的编程语言,也就是说它在同一时间只能执行一个任务。然而,现代 Web 应用经常需要处理大量的异步操作,如用户输入、网络请求、定时器等。为了确…...

Stream流的终结方法(二)——collect
1.Stream流的终结方法 2. collect方法 collect方法用于收集流中的数据放到集合中去,可以将流中的数据放到List,Set,Map集合中 2.1 将流中的数据收集到List集合中 package com.njau.d10_my_stream;import java.util.*; import java.util.f…...

【C语言系统编程】【第一部分:操作系统知识】1.1.操作系统原理
第一部分:操作系统知识 1.1 操作系统原理 1.1.1 进程管理 1.1.1.1 进程的概念与生命周期 进程是程序在计算机中的一次执行实例,包括了程序的代码、数据、以及运行的上下文环境。进程管理是操作系统的核心任务之一。 作用:管理所有执行中…...

基于Java+VUE+echarts大数据智能道路交通信息统计分析管理系统
大数据智能交通管理系统是一种基于Web的系统架构,通过浏览器/服务器(B/S)模式实现对城市交通数据的高效管理和智能化处理。该系统旨在通过集成各类交通数据,包括但不限于车辆信息、行驶记录、违章情况等,来提升城市管理…...

leetcode-42. 接雨水 单调栈
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表…...

ThinkPHP和PHP的区别
文章目录 ThinkPHP和PHP的区别一、引言二、PHP简介1、第一步1.1、示例代码 三、ThinkPHP简介2、第二步2.1、特点2.2、示例代码 四、总结 ThinkPHP和PHP的区别 一、引言 在Web开发领域,PHP是一种广泛使用的开源脚本语言,而ThinkPHP则是一个基于PHP的MVC…...

clientWidth,offsetWidth,scrollHeight
clientWidth: offsetWidth: scrollHeight:...

SVN版本回退
SVN 版本回退三种方法: Update item to this version 假设我们的项目文件一共有8个版本,它版本号分别是1,2,3,4,5,6,7,8。 这个选项的作用是将文件版本更新到对应所选的…...
IDEA关联Tomcat
一、Tomcat服务器 web服务器,就是运行web项目的容器 即运行java代码的一个容器 webapp(web应用程序) --> 就是我们写的javaweb项目 Tomcat 是Apache 软件基金会(Apache Software Foundation)下的一个核心项目,免费开源、并支持Servlet 和J…...

MongoDB mongoose 的 save、insert 和 create 方法的比较
目录 save 方法 insert 方法 create 方法 使用会话和事务 总结 在本文中,我们将介绍 MongoDB 中使用 mongoose 操作 数据库时的三种常见方法:save、insert 和 create。这些方法可以用于将数据存储到 MongoDB 数据库中,并且在一定程度上具…...

Maven安装使用
说明:Maven是Apache旗下的一个开源项目,是一款用于管理和构建java项目的工具。一般来说,它帮助我们管理依赖、构建项目。本文介绍在Windows系统下安装Maven。 下载&安装&验证 下载 首先,在Maven官网(https:…...

微信第三方开放平台接入本地消息事件接口报错问题java.security.InvalidKeyException: Illegal key size
先看报错: java.security.InvalidKeyException: Illegal key sizeat javax.crypto.Cipher.checkCryptoPerm(Cipher.java:1039)at javax.crypto.Cipher.implInit(Cipher.java:805)at javax.crypto.Cipher.chooseProvider(Cipher.java:864)at javax.crypto.Cipher.in…...

如何只修改obsidian图片链接为markdown
如何只修改obsidian图片链接为markdown 前言插件配置 使用注意 前言 适合有一定了解obsidian用法和插件市场,还有相对路径的人 插件 在obsidian插件市场搜索—开梯子 配置 首先使用ctrlp打开命令面板,也可以在左侧通过图标打开命令面板,…...
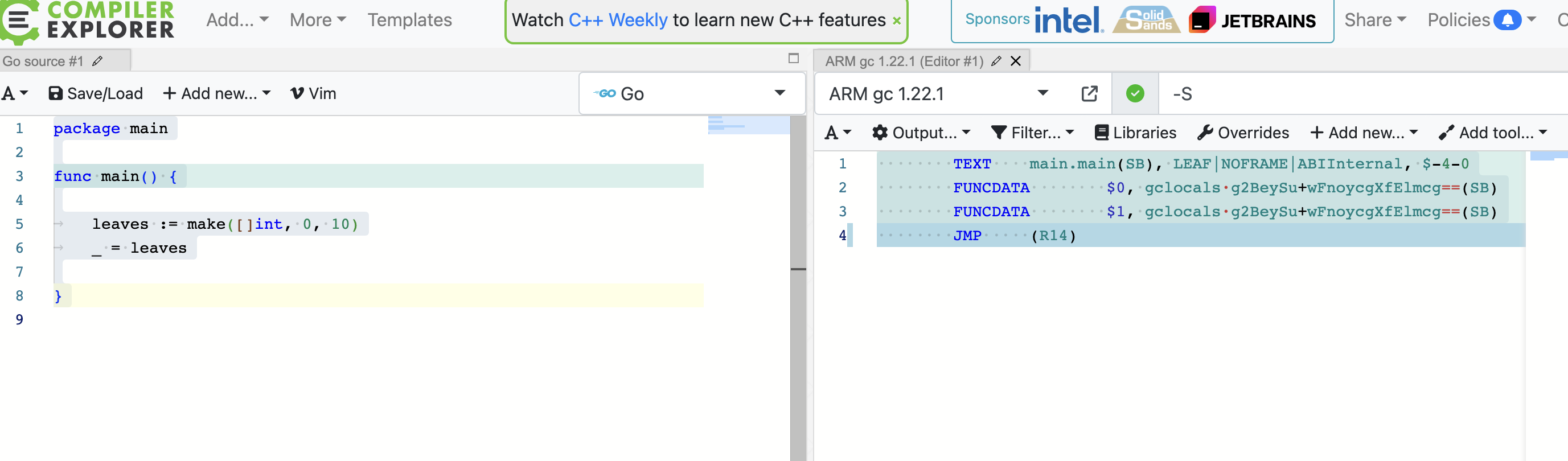
AI不可尽信
看到某项目有类似这样的一段代码 leaves : make([]int, 10) leaves leaves[:0]没理解这样的连续两行,有何作用? 初始化一个长度和容量都为10的切片,接着把切片长度设置为0 即如下demo: (在线地址) package mainimport "fmt"func main() {leaves : make([]int, 1…...
[C++]使用纯opencv部署yolov11旋转框目标检测
【官方框架地址】 GitHub - ultralytics/ultralytics: Ultralytics YOLO11 🚀 【算法介绍】 YOLOv11是一种先进的对象检测算法,它通过单个神经网络实现了快速的物体检测。其中,旋转框检测是YOLOv11的一项重要特性,它可以有效地检…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
