数据结构：AVL树

前言

学习了普通二叉树，发现普通二叉树作用不大，于是我们学习了搜索二叉树，给二叉树新增了搜索、排序、去重等特性，
但是，在极端情况下搜索二叉树会退化成单边树，搜索的时间复杂度达到了O(N)，这是十分不利的，
所以，牛人们又提出了新的数据结构：AVL树（平衡搜索二叉树），给搜索二叉树新增了平衡的特性，控制左右子树的高度，是搜索二叉树处于平衡的状态，避免出现极端情况。

AVL树的发明者是两位俄罗斯数学家G.M.Adelson-Velskii和E.M.Landis，为了几年他们在1962年提出该数据结构，就命名为AVL树。

---

AVL树的特性

AVL树要求任意节点的左右子树的高度差的绝对值不超过1.
为什么拥有该特性AVL树就可以保持平衡呢？这里需要数学证明，就不解释了，理解原理后，就很容易理解。

一棵AVL树是具有以下性质的二叉搜索树：

1. 它的左右子树都是AVL树
2. 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

注意：在这里，我们引入一个变量，平衡因子（balance factor），用来记录左右子树的高度差，
这里我们记录右子树的高度减左子树的高度。
当然，也可以有其他的思路来替代平衡因子。

---

AVL树节点的定义（以KV型为例）

template<class K, class V>
struct AVLTreeNode
{AVLTreeNode<K,V>* _left = nullptr;//左子节点AVLTreeNode<K, V>* _right = nullptr;//右子节点AVLTreeNode<K, V>* _parent = nullptr;//父亲节点pair<K, V> _kv;//数据int _bf = 0;//平衡因子AVLTreeNode(const pair<K, V>& kv):_kv(kv){}
};

注意：AVL树使用三叉链实现，多了一个parent指针，用来记录父亲节点，方便使用。

---

AVL树的插入（核心）

AVL树是在搜索二叉树上面进行升级，所以查找的方法和搜索二叉树类似，大了就向右子树走，小了就往左子树走。

因为这里多了parent指针和bf，在插入之后都需要进行维护。（天下没有白吃的午餐，使用的时候方便，维护起来就麻烦了QAQ）

parent指针处理起来很简单，我们这里主要讲bf如何控制。

bf有三种取值 0 ， - 1 ， 1
当我们在节点的右侧插入的时候，节点的bf++，在节点的左侧插入的时候，节点的bf–。

在右边插入，右子树的高度增加，bf++，在左边插入的时候，左子树的高度增加，bf–

这是毫无疑问的，以下都基于此。

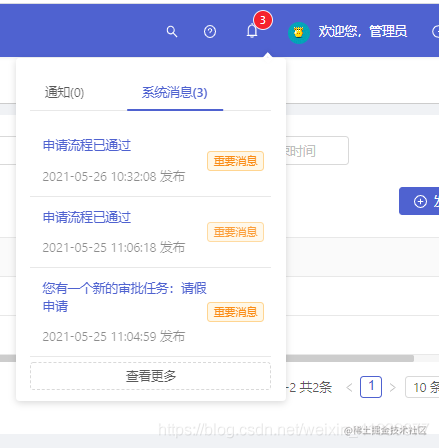
OK，更新完当前节点之后，bf就维护好了吗？
哪有这么简单QAQ

在插入后cur的bf更新为1，仅仅如此吗？
看这张图，parent的bf也要从1变成2了。

所以，在更新完cur节点的bf后，还需要根据情况确定是否要继续向上更新

具体是否要更新，主要是看子树的高度有没有发生变化

有哪些情况呢？

1. cur插入后更新为0
   说明原来是1 或者 -1，在较短的那一条边上新增了新节点，将cur节点变平衡了，
   这样的话，那高度就没有增加，不会影响到子树的高度，就不需要向上更新bf了。
2. cur插入后更新为 1，-1
   说明原来是0，原来是平衡的，插入新节点后破坏了平衡，子树高度发生了变化，
   所以需要向上更新bf。
3. cur插入后更新为 2，-2
   当更新为2，-2后，发现违反了AVL树的规则，不再是一颗AVL树，我们就需要进
   行特殊操作来维护AVL树的性质了。（这里，我们采用旋转）

---

AVL树的旋转（最难的部分）

AVL树的旋转是AVL树这个数据结构的亮点，掌握了这一点之后，才会理解这种数据结构有多么精妙。

从深层上看，AVL树的旋转分为四种情况，我们画图来分析。（由于实际情况太多太多，我们这里画抽象图）

左单旋

这里h >= 0
我们在最右边插入一个节点，使AVL树的右侧完全倾斜，那么我们就需要向左侧旋转了。
如何向左旋转呢？

我们将三个需要用到的节点命名一下，分别为parent，subR，以及subRL
根据搜索二叉树的性质，我们知道subRL > parent ，但是小于subR，所以就可以进行左单旋而不会破坏搜索的性质

左单旋就是
先将subRL插入到parent的右边
接着将parent插入到subR的左边

成功旋转之后图形变成下面的样子

这样左右子树的高度就一样了，重新将AVL树调整平衡了
这里还有非常多的代码细节，例如空指针，parent指针的维护等等需要处理，这里大家可以先尝试根据思路写出代码，再跟后面的代码进行比较，看看是否写对了。

这里只简单讲一下平衡因子的维护。
可以看到，在左单旋只会影响parent和subR两个节点的bf，且旋转后皆为0，故不用向上继续调整。

---

右单旋

右单旋和左单旋类似，是对称的，这里只简单画出抽象图，相信读者能够自己理解。

右单旋就是处理左边完全倾斜的情况，向右边旋转，进而调整平衡。
代码依旧在文末尾给出。

---

右左双旋

顾名思义，先右单旋后左单旋构成右左双旋。
相信聪明的小伙伴，在看到左单旋和右单旋的时候，就会发现这两种情况都是插入在最右边和最左边造成完全倾斜。
而插入在右子树的左边和左子树的右边都没有列举出来。

这里右左双旋就是应对插入在右子树的左边这种情况的，显然，左右双旋就是应对插入在左子树的右边那种情况的，这里讲右左双旋，左右双旋留给大家自己思考。

左单旋和右单旋都不适合这种情况，根本原因在于，这种情况并不是完全倾斜，很简单嘛，
你不是完全倾斜，我强行让你变成完全倾斜，不就可以使用左单旋或者右单旋了嘛。

对于这种情况，我们可以看到是subRL太高了，导致的不平衡，我们将subRL旋转到subR的位置岂不是可以造成完全倾斜了吗？

这右单旋不就来了嘛，使用右单旋就将subRL的右插入到subR的左，再将subR插入到subRL的右即可。

右单旋完了之后，就是下面的图形

映入眼帘的就是右边太高了，出现了完全倾斜，直接左单旋调整平衡即可。

这里同样有很多代码细节，要维护好parent和bf，以及处理好空指针的特殊情况。

这里还是只简单讲一下bf的维护
我们以终为始，只看旋转前和旋转后的两幅图。

我们可以看到只有三个节点60 30 90的bf发生了变化。
也就是只有parent，subR，subRL三个节点的bf发生了变化。
这里最后subRL和subR的bf 变成了0，parent的bf变成了-1。
但是，一定是这样吗？
这中情况是在c子树上插入新节点，如果在b上插入新节点。
a和b的高度都是h，parent的bf就是0，c的高度是h-1，d的高度是h，subR的bf就是1

问题就在于是在subRL的左子树插入还是右子树插入新节点。
如何分辨?
很简单，去观察subRL的旋转前的bf
如果是1，就是在右子树插入，如果是-1，就是在左子树插入

---

左右双旋

大体和右左双旋类似，所以这里简单画个抽象图，相信读者能够自行理解。

这里就是新节点插入在了左子树的右边，导致不平衡，先左单旋调整成完全倾斜，在右单旋调整至平衡。

---

代码

#include <assert.h>
#include <iostream>using namespace std;namespace Avltree//命名空间名不能和类名相同，不然会发生命名冲突
{template<class K, class V>struct AVLTreeNode{AVLTreeNode<K,V>* _left = nullptr;AVLTreeNode<K, V>* _right = nullptr;AVLTreeNode<K, V>* _parent = nullptr;pair<K, V> _kv;int _bf = 0;//平衡因子AVLTreeNode(const pair<K, V>& kv):_kv(kv){}};template<class K,class V>class AVLTree{typedef AVLTreeNode<K, V> Node;private:Node* _root = nullptr;//开始的时候要给空，不然就是野指针了void RotateL(Node* parent)//左单旋{Node* subR = parent->_right;Node* subRL = subR->_left;Node* pparent = parent->_parent;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;if (pparent == nullptr){subR->_parent = nullptr;_root = subR;}else{if (pparent->_left == parent){pparent->_left = subR;}else{pparent->_right = subR;}subR->_parent = pparent;}parent->_bf = 0;subR->_bf = 0;}void RotateR(Node* parent)//右单旋{Node* subL = parent->_left;Node* subLR = subL->_right;Node* pparent = parent->_parent;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;if (pparent == nullptr){subL->_parent = nullptr;_root = subL;}else{if (pparent->_left == parent){pparent->_left = subL;}else{pparent->_right = subL;}subL->_parent = pparent;}parent->_bf = 0;subL->_bf = 0;}void RotateRL(Node* parent){RotateR(parent->_right);RotateL(parent);}void RotateLR(Node* parent){RotateL(parent->_left);RotateR(parent);}void InOrder(Node* root){if (root == nullptr)return;InOrder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;InOrder(root->_right);}public:void inorder(){InOrder(_root);}bool find(const K& key){Node* cur = _root;while (cur){if (key > cur->_kv.first){cur = cur->_right;}else if (key < cur->_kv.first){cur = cur->_left;}else{return true;}}return false;}bool insert(const pair<K, V>& kv){if (_root == nullptr)//插入的时候要特殊处理空树{_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;//如果已经在，那就插入失败，返回false}}//找到了，开始插入；cur = new Node(kv);cur->_parent = parent;if (kv.first > parent->_kv.first)//插入的节点很大，插在右边{parent->_bf++;parent->_right = cur;}else{parent->_bf--;parent->_left = cur;}//插入完成，调整平衡因子；while (parent){if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//开始旋转if (parent->_bf == 2 && cur->_bf == 1)//右边太高了，左单旋{RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1)//左边太高了，右单旋{RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == -1)//右边高，但是偏了{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateRL(parent);if (bf == 0){parent->_bf = subR->_bf = subRL->_bf = 0;}else if (bf == 1){subRL->_bf = subR->_bf = 0;parent->_bf = -1;}else if(bf == -1){subRL->_bf = parent->_bf = 0;subR->_bf = 1;}else{assert(false);}}else if (parent->_bf == -2 && cur->_bf == 1)//左边高但是偏向右边{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateLR(parent);if (bf == 0){parent->_bf = subL->_bf = subLR->_bf = 0;}else if (bf == 1){subL->_bf = -1;parent->_bf = subLR->_bf = 0;}else if(bf == -1){subLR->_bf = subL->_bf = 0;parent->_bf = 1;}else{assert(false);}}}else{assert(false);//走到这里来就出现错误了}}return true;}};
}

---

对于AVL树的删除，和插入类似，但是更加复杂些，限于篇幅，就暂且不讲AVL树的删除了，感兴趣的读者可以参考《算法导论》和《数据结构（用面向对象方法与C++语言描述）》（殷人昆版）。

---