探索 Python 高精度计算的奥秘:mpmath 库全解析
文章目录
- 探索 Python 高精度计算的奥秘:mpmath 库全解析
- 背景:为何选择 mpmath?
- 第二部分:mpmath 是什么?
- 第三部分:如何安装 mpmath?
- 第四部分:mpmath 函数使用示例
- 第五部分:实际应用场景
- 第六部分:常见问题与解决方案
- 第七部分:总结

探索 Python 高精度计算的奥秘:mpmath 库全解析
背景:为何选择 mpmath?
在科学计算、工程模拟、数据分析等领域,对数值精度的要求往往非常高。Python 虽然有广泛的应用,但其内置的浮点数精度有限。这时,mpmath 库应运而生,它提供了任意精度的浮点数计算能力,能够满足高精度计算的需求。
第二部分:mpmath 是什么?
mpmath 是一个开源的 Python 库,用于任意精度的实数和复数浮点数算术运算。它支持复杂的数学函数计算,并且可以作为 Python 的 math 和 cmath 模块的高精度替代品。
第三部分:如何安装 mpmath?
安装 mpmath 非常简单,可以通过 pip 命令行工具进行安装:
pip install mpmath
这样就能够在你的 Python 环境中使用 mpmath 了。
第四部分:mpmath 函数使用示例
-
设置精度:
from mpmath import mp mp.dps = 50 # 设置小数点后保留 50 位这里
dps表示十进制精度,用于控制计算的精度。 -
计算圆周率:
pi = mp.pi print(pi)使用 mpmath 计算圆周率至 50 位小数。
-
计算指数:
exp_value = mp.exp(1) print(exp_value)计算 e 的自然对数。
-
计算对数:
log_value = mp.log(10) print(log_value)计算 10 的自然对数。
-
计算三角函数:
sin_value = mp.sin(mp.pi / 2) print(sin_value)计算 π/2 的正弦值。
第五部分:实际应用场景
-
高精度圆周率计算:
from mpmath import mp mp.dps = 100 print(mp.pi)用于科研或教育中需要极高精度的圆周率值。
-
金融计算:
from mpmath import mp mp.dps = 30 future_value = mp.fv(0.05, 10, -1000) print(future_value)计算未来价值,常用于金融分析。
-
物理常数计算:
from mpmath import mp mp.dps = 50 speed_of_light = mp.sqrt(1 / (2.99792458e8**2)) print(speed_of_light)计算光速,用于物理研究和教育。
第六部分:常见问题与解决方案
-
精度不足:
- 错误信息:计算结果与预期有较大偏差。
- 解决方案:增加
dps值,提高计算精度。
mp.dps = 100 # 增加精度 -
性能问题:
- 错误信息:计算速度慢。
- 解决方案:使用 gmpy 库加速或减少精度要求。
import gmpy -
复数运算错误:
- 错误信息:复数运算结果不准确。
- 解决方案:确保复数输入格式正确。
from mpmath import mpc z = mpc(1, 2) result = z**2 print(result)
第七部分:总结
mpmath 是一个功能强大的 Python 库,它通过提供任意精度的计算能力,极大地扩展了 Python 在科学计算领域的应用。无论是在学术研究还是工业应用中,mpmath 都能提供稳定和可靠的数值计算支持。通过本文的介绍,希望你能更好地理解和使用 mpmath,解决实际问题。
如果你觉得文章还不错,请大家 点赞、分享、留言 下,因为这将是我持续输出更多优质文章的最强动力!

相关文章:

探索 Python 高精度计算的奥秘:mpmath 库全解析
文章目录 探索 Python 高精度计算的奥秘:mpmath 库全解析背景:为何选择 mpmath?第二部分:mpmath 是什么?第三部分:如何安装 mpmath?第四部分:mpmath 函数使用示例第五部分࿱…...

<<迷雾>> 第10章 用机器做一连串的加法(1)--使用两排开关分别给出被加数和加数 示例电路
info::操作说明 鼠标单击逻辑输入切换 0|1 状态 primary::在线交互操作链接 https://cc.xiaogd.net/?startCircuitLinkhttps://book.xiaogd.net/cyjsjdmw-examples/assets/circuit/cyjsjdmw-ch10-01-5-bit-adder.txt 原图...
Stable Diffusion最新版nowebui的api使用详解
最近在使用stable diffusion最新版的Stable Diffusion WebUI Forge进行api调用,下面来一步一步的进行展开吧!!! 1、下载lllyasviel/stable-diffusion-webui-forge GitHub - lllyasviel/stable-diffusion-webui-forgeContribute to lllyasviel/stable-diffusion-webui-for…...
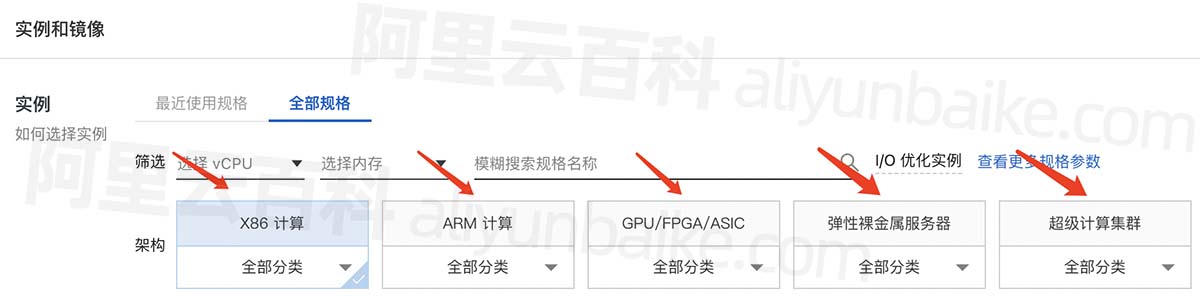
云服务器架构详解:X86计算_ARM_GPU/FPGA/ASIC_裸金属_超级计算集群
阿里云服务器架构有什么区别?X86计算、ARM计算、GPU/FPGA/ASIC、弹性裸金属服务器、超级计算集群有什么区别?阿里云服务器网aliyunfuwuqi.com分享云服务器ECS架构详细说明: 阿里云服务器ECS架构说明 阿里云服务器ECS架构 X86计算 X86计算架…...

高级java每日一道面试题-2024年10月4日-数据库篇-MySQL索引底层结构为什么使用B+树?
如果有遗漏,评论区告诉我进行补充 面试官: MySQL索引底层结构为什么使用B树? 我回答: 该面试题本质还是在考察B树的数据结构和在数据库系统中的应用,下边是详细的回答。 B树的基本特性 B 树的结构特点 非叶子节点只存储键值信息,不存储…...

【JVM】内存分析工具JConsole/Visual VM
1 缘起 日常补充JVM调优,调优实践前需要学习一些理论做支撑, JVM调优三步:理论>GC分析>JVM调优, 我们会有一些玩笑话说,做了这么久Java开发,做过JVM调优吗? 做过,面试时。当然…...

一静 、二平 、三忍 、四让、五淡
一静 、二平 、三忍 、四让、五淡。 作者:儒风君 来源:儒风大家(ID: rufengdajia) 古人为人、处事、修身,都有独特的章法。 一静、二平、三忍、四让、五淡。 说透中国人的大智慧。 1 静 《道德经》里讲:“清静为天下正。”…...
:函数的本质)
js 深入理解函数(一):函数的本质
目录 概述1. 箭头函数2. 函数名 :指向函数的指针3. 理解参数3.1 arguments 对象的作用3.2 arguments 的注意点3.3 箭头函数中的参数 4. 没有重载5. 默认参数值5.1 ES 6 支持显示定义默认参数5.2 传 undefined 等于没有传值5.3 arguments 不反映参数默认值5.4 默认值…...

MySql表结构设计
创建 create table 表名(字段1 字段类型 [约束] [comment 字段1注释],...) [comment 表注释];约束是作用于表中字段上的规则,用于限制存储在表中的数据。它的目的是保证数据库中数据的正确性、有效性和完整性。 约束描述关键字非空约束限制该字段不能为nullnot nu…...

java:pdfbox 3.0 去除扫描版PDF中文本水印
官网下载 https://pdfbox.apache.org/download.html下载 pdfbox-app-3.0.3.jar cd D:\pdfbox 运行 java -jar pdfbox-app-3.0.3.jar java -jar pdfbox-app-3.0.3.jar Usage: pdfbox [COMMAND] [OPTIONS] Commands:debug Analyzes and inspects the internal structu…...
-替换requests的python库httpx)
python知识点100篇系列(17)-替换requests的python库httpx
Requests 是使用 Apache2 Licensed 许可证的 基于Python开发的HTTP 库,其在Python内置模块的基础上进行了高度的封装,使用Requests可以轻而易举的完成浏览器可有的任何操作。 但是在python3.6之后,出现了一个requests的替代选项; httpx httpx是Python新一代的网络请求库…...

python 实现graph list图列算法
graph list图列算法介绍 图列(Graph List)算法通常指的是在图的表示中,使用列表(List)或更具体地说,邻接表(Adjacency List)来表示图的一种算法。邻接表是图的一种常见表示方法&…...

LFU算法 初始频率 动态频率
LFU(Least Frequently Used)算法是一种缓存淘汰策略,其核心思想是根据数据的访问频率来决定淘汰哪些数据。具体来说, LFU算法认为如果一个数据在过去一段时间内被访问的次数很少,那么它在未来被再次访问的概率也…...

Spring Boot 进阶-详解SpringBoot的复杂数据校验规则
在之前的文章中,我们介绍了SpringBoot整合JSR-303规则来完成数据校验操作。接下来我们来聊一聊关于数据校验的具体用法。 之前的文章中举过一个简单的例子通过学生信息提交的例子来介绍了关于数据校验如何去做。那么接下来这篇文章,我们就来看看对于一些复杂的数据校验如何完…...

wsl环境下安装Ubuntu,并下载MySQL5.7
安装操作需root权限,切换root用户有两种方式: 1-通过 sudo su - ,切换到root用户(登录后长期有效)。 2-在每一个命令前加上sudo,临时提升权限(仅对一条命令有效)。 1、下载apt仓库…...

倪师学习笔记-天纪-01
一、概要 介绍课程内容,介绍部分概念 二、具体内容 1、天纪内容 天机道:看象,使用斗数等工具人间道:看卦,使用易经地脉道:看风水地理 2、神 神与形对应,形是神的实例,神是形的…...

深入理解缓存穿透、缓存击穿和缓存雪崩
在现代分布式系统中,缓存是提升系统性能和减轻数据库负载的重要组件。然而,在实际应用中,我们可能会遇到一些缓存问题,如缓存穿透、缓存击穿和缓存雪崩。本文将详细探讨这三种缓存问题的原理、影响以及解决方案。 一,…...

【玩转动态规划专题】70. 爬楼梯【简单】
【玩转动态规划专题】70. 爬楼梯【简单】 1、力扣链接 https://leetcode.cn/problems/climbing-stairs/description/ 2、题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 示例 1&…...

前端开发设计模式——组合模式
目录 一、组合模式的定义和特点 1.定义 2.特点: 二、组合模式的实现方式 1.定义抽象组件类 2.创建叶节点类 3.创建组合类: 三、组合模式的应用场景 1.界面布局管理 2.菜单系统构建 3.组件库开发 四、组合模式的优点 1.简化客户端代码 2.增…...

初探OceanBase 4.x单机环境下如何进行主备架构搭建
本文来自OceanBase 用户的体验分享 (以下简称 OB),已经开源了3年左右,其间从3.x版本演进至4.x版本,发生了许多变化。对一个DBer而言,最为关切的是如何高效运用OB,以及是否能实现如同应用MySQL般…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...
