自定义类型结构体(上)
目录
- 结构体类型的声明
- 结构体的概念
- 结构体的声明
- 特殊的声明
- 结构的自引用
- 结构体变量的创建和初始化
- 结构成员访问操作符
结构体类型的声明
结构体的概念
结构体是一些值的集合,这些值称为成员变量。结构的每个成员可以是不同类型的变量
举个例子:杰克的英语只考了60分,你需要将杰克考试的信息填在一张表中,那么表中的信息应该有姓名 班级 学号 分数,表就是杰克信息的集合,而姓名班级等等则都是表中成员,姓名具体对应的名称为杰克,则就称为成员变量
从上面的例子不难看出,结构体中的成员可以是不同类型的变量,我们再回想一下数组,数组的每个成员是不是都是同一种类型的变量,由于结构体和数组都是一些值的集合,因此我推断出数组是结构体的特殊情况(虽然表现的形式有区别)
结构体的声明
struct tag(tag为你自己设定的名称)
{member-list;//成员列表
}variable-list;//变量列表(可有可无)
我们依然用上面的例子:
//描述杰克的英语成绩
struct Stu
{char name[20];//名字int class[20];//班级char id[20];//学号char Score[20];//分数
};
如果我们需要对杰克 约翰 等人填写信息的话,我们需要创建多个变量
方式一:
struct Stu
{char name[20];//名字int class[20];//班级char id[20];//学号char Score[20];//分数
}s1,s2,s3;//是三个结构体变量(是全局变量)
方式二:
struct Stu
{char name[20];//名字int class[20];//班级char id[20];//学号char Score[20];//分数
}
int main()
{
struct stu s4,s5,s6//局部变量
return 0;
}
特殊的声明
在声明结构的时候,可以不完全的声明比如:
//匿名结构体类型
struct
{int a;char b;float c;
}x;//只能用一次
struct
{int a;char b;float c;
}a[20], * p;//只能用一次
我们来看一段代码:
struct
{char name[20]
}a;
struct
{char name[20]
}*p;
int main()
{p = &a;return 0;
}
虽然两个结构体里面的变量是一样的,但是在运行时VS仍然会把他认为是两种不同的结构体,既是你将b结构体的地址传给p,也不能让p变成b的结构体
结构的自引用
在结构中包含⼀个类型为该结构本身的成员是否可以呢?
比如:
struct Node
{int data;struct Node next;
};
仔细分析,其实是不行的,因为一个结构体中再包含一个同类型的结构体变量,这样结构体变量的大小就会无穷的大,是不合理的
在学到这里时我其实想到了一个数学例子

虽然这个结果是可以求极限的,但是这个嵌套的方式和这道题非常类似
正确的自引用方式:
struct Node
{int data;struct Node* next;
};
如果我们用的是同类型结构体指针struct Node* next,我们就可以算出内存大小了,因为*next是具体指向一个地址,有且只有一个,所以内存不会无限大
在结构体自引用使用的过程中,夹杂了typedef对匿名结构体类型重命名,也容易引入问题,看看下面的代码
typedef struct
{int data;Node* next;
}Node;
结果是不行的,因为Node是对前面的匿名结构体类型的重命名产生的,但是在匿名结构体内部提前使用Node类型来创建成员变量,导致结构体还没有完全创建出来就拿出来用,这很明显是不行的.
解决方案如下:定义结构体不要使用匿名结构体了
typedef struct Node
{int data;struct Node* next;
}Node;
这里要和上面的例子要区别开,因为在一开始我们就让结构体类型为Node,所以在中间我们可以直接拿来用
结构体变量的创建和初始化
有了结构体类型,那如何定义变量,其实很简单,结构体变量的初始化使用{}
struct Point//描述坐标的一个点
{int x;int y;
}p1; //声明类型的同时定义变量p1struct Point p2; //定义结构体变量p2//初始化:定义变量的同时赋初值。
struct Point p3 = { x, y };struct Stu //类型声明
{char name[15];//名字int age; //年龄
};
struct Stu s = { "zhangsan", 20 };//初始化struct Node
{int data;struct Point p;struct Node* next;
}n1 = { 10, {4,5}, NULL }; //结构体嵌套初始化
//如果要打印struct Node中的struct Point p的话
printf("%d %d",Node.p.x,Node.p.y)struct Node n2 = { 20, {5, 6}, NULL };//结构体嵌套初始化
指示器初始化方式(C99),这种方式允许不是按照成员顺序初始化
struct Stu
{char name[15];int age;
};
struct Stu s = {.age=20, .name="zhangsan"};//初始化
.age就可以准确的将20赋值给age,这样就可以不按照成员顺序初始化了
结构成员访问操作符
结构成员访问操作符有两个一个是 . ,一个是 -> .
形式如下:
结构体变量.成员变量名
结构体指针—>成员变量名
我们看一个例子:
#include <stdio.h>
#include <string.h>
struct Stu
{char name[15];//名字int age; //年龄
};
void print_stu(struct Stu s)
{printf("%s %d\n", s.name, s.age);
}
void set_stu(struct Stu* ps)
{strcpy(ps->name, "李四");ps->age = 28;
}
int main()
{struct Stu s = { "张三", 20 };print_stu(s);set_stu(&s);print_stu(s);return 0;
}

相关文章:

自定义类型结构体(上)
目录 结构体类型的声明结构体的概念结构体的声明特殊的声明结构的自引用 结构体变量的创建和初始化结构成员访问操作符 结构体类型的声明 结构体的概念 结构体是一些值的集合,这些值称为成员变量。结构的每个成员可以是不同类型的变量 举个例子:杰克的英语只考了6…...

b站-湖科大教书匠】4 网络层 - 计算机网络微课堂
【b站-湖科大教书匠】4 网络层 - 计算机网络微课堂_湖科大的计算机网络网课-CSDN博客...

国际 Android WPS Office v18.13 解锁版
WPS Office 移动版,设计不断优化,性能再次提升!融入Google Android最新设计标准,Material Design设计风格,完美支持沉浸式!简化文档操作,全新移动办公力作。全新界面更清晰舒适,功能…...
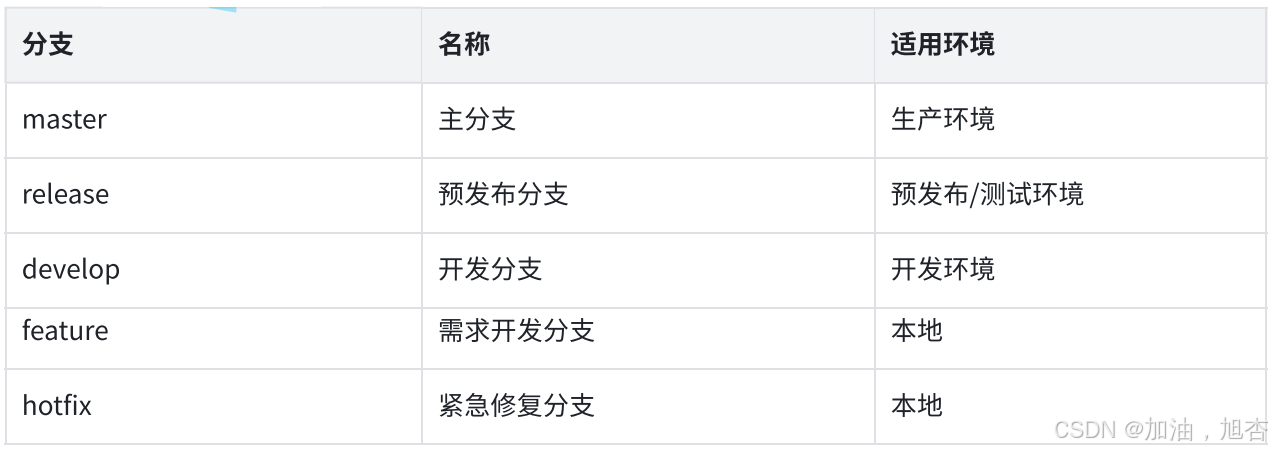
【中间件学习】Git的命令和企业级开发
一、Git命令 1.1 创建Git本地仓库 仓库是进行版本控制的一个文件目录。我们要想对文件进行版本控制,就必须创建出一个仓库出来。创建一个Git本地仓库对应的命令是 git init ,注意命令要在文件目录下执行。 hrxlavm-1lzqn7w2w6:~/gitcode$ pwd /home/hr…...

FTP连接池与多线程FTP上传下载算法(Java)
设计一个能够处理FTP连接池在多线程环境下,尤其是涉及到故障重连时避免竞争条件的算法,需要综合考虑线程同步、连接状态管理和重试机制。以下是一个设计思路和实现方案: 设计思路 连接池管理: 维护一个连接池,其中包含多个FTP连接对象。每个FTP连接对象需有状态标记(如…...

Spring Cloud微服务详解
Spring Cloud微服务详解 在当今的数字化时代,微服务架构已成为构建大型、复杂应用系统的主流方式。Spring Cloud,作为微服务领域的一颗璀璨明星,以其强大的功能和灵活的架构,吸引了无数开发者的目光。本文将深入探讨Spring Cloud…...
)
QT学习笔记1.2(QT的应用)
QT原生用于c的开发, 主要应用于电脑、桌面手机桌面软件的开发,主要是widget样式模板。 Qt Widgets、Qt Quick 和 Qt for Python 是 Qt 框架中的三种不同的技术,分别用于不同的应用场景。以下是它们的详细介绍和对比: 1. Qt Widg…...

数学建模算法与应用 第1章 线性规划
第1章 线性规划 线性规划是数学规划领域的重要分支,广泛应用于资源配置、生产计划、物流管理等领域。它主要用于解决如何在满足一定约束条件下,使目标函数(如成本、利润等)达到最大或最小的问题。第一章将介绍线性规划的基本概念…...

使用 systemd 设置 PHP 程序为服务
使用 systemd 设置 PHP 程序为服务 在现代 Linux 系统中,systemd 是用于管理和控制服务的标准工具。通过 systemd,我们可以轻松地将 PHP 程序配置为后台运行的系统服务,从而实现自动化启动、重启和日志记录等功能。本文将介绍如何为 PHP 程序…...

HRNET模型实现钢板表面缺陷检测
关于深度实战社区 我们是一个深度学习领域的独立工作室。团队成员有:中科大硕士、纽约大学硕士、浙江大学硕士、华东理工博士等,曾在腾讯、百度、德勤等担任算法工程师/产品经理。全网20多万粉丝,拥有2篇国家级人工智能发明专利。 社区特色…...

28 基于51单片机的两路电压检测(ADC0808)
目录 一、主要功能 二、硬件资源 三、程序编程 四、实现现象 一、主要功能 基于51单片机,通过ADC0808获取两路电压,通过LCD1602显示 二、硬件资源 基于KEIL5编写C代码,PROTEUS8.15进行仿真,全部资源在页尾,提供…...

SpringBootTest Mockito 虚实结合编写测试
SpringBootTest & Mockito 虚实结合测试 起因 单一使用mockito,会出现很多mock困难的问题,导致测试编写过程太长,太恶心 单一使用springboottest,会遇到需要外部接口的地方,这个时候就非得去真实调用才行。也很恶…...
)
国内外网络安全政策动态(2024年9月)
国内网络安全政策动态 ▶︎ 1.三项智能网联汽车强制性国家标准正式发布 9月4日,工业和信息化部组织制定的GB 44495—2024《汽车整车信息安全技术要求》、GB 44496—2024《汽车软件升级通用技术要求》和GB 44497—2024《智能网联汽车 自动驾驶数据记录系统》三项强制…...

使用Android studio进行Unit Test中遇到的问题记录
1、模块本身代码运行不起来 提示: Cannot resolve method ‘getVolumes’ in ‘StorageManager’ Cannot resolve method ‘registerListener’ in ‘StorageManager’ Cannot resolve method ‘unregisterListener’ in ‘StorageManager’ 查看Android 源码&…...

智能运维与问题诊断工具:提升生产环境的安全稳定性
引言 在当今复杂的IT环境中,确保生产系统的安全稳定运行是一项巨大挑战。随着技术的进步,智能运维和问题诊断工具应运而生,为IT团队提供了强大的支持。本文将介绍一系列先进的工具,这些工具利用人工智能、机器学习和自动化技术,帮助组织提高系统可靠性、加速问题解决、优…...

【MAUI】CommunityToolkit社区工具包介绍
一、为什么需要声明式开发 .NET的MVVM,始于WPF,很古典,它甚至可能是现代前端框架“声明式开发”的鼻祖。声明式开发,之所以出现,是因为命令式开发在UI层和代码层上无法解耦的问题。如下图所示: 1、命令式开发:后台代码需要调用UI层的控件(label.Text),如果更新UI层…...

【答疑解惑】图文深入详解undo和redo的区别及其底层逻辑
题记:最近有些人问我,undo和redo到底是什么关系,他们中不乏已经入行3-4年的同学,今天咱们就来深入探讨下到底什么是undo和redo,他们分别做什么,底层逻辑原理是什么等等。 1. undo 1.1 undo的存储结构 Un…...

低通滤波、反相放大器电路
1 简介 这种可调低通滤波、反相放大器电路可将信号电平放大 26dB 或 20V/V。R2 和 C1 会为此电路设置截止频率。此电路的频率响应与无源 RC 滤波器的相同,除非输出按放大器的通带增益进行放大。低通滤波器通常用于音频信号链,此滤波器有时也称为低音增强…...

SpringBoot助力服装生产流程优化
1 绪论 1.1 研究背景 当今时代是飞速发展的信息时代。在各行各业中离不开信息处理,这正是计算机被广泛应用于信息管理系统的环境。计算机的最大好处在于利用它能够进行信息管理。使用计算机进行信息控制,不仅提高了工作效率,而且大大的提高…...

【机器学习】线性回归算法简介 及 数学实现方法
线性回归 简介 利用 回归方程(函数) 对 一个或多个自变量(特征值)和因变量(目标值)之间 关系进行建模的一种分析方式。 数学公式: ℎ_(w) w_1x_1 w_2x_2 w_3x_3 … b w^Txb 概念 利用回归方程(函数) 对 一个或多个自变量(特征值)和因变量(目标值)之间 关…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

表单设计器拖拽对象时添加属性
背景:因为项目需要。自写设计器。遇到的坑在此记录 使用的拖拽组件时vuedraggable。下面放上局部示例截图。 坑1。draggable标签在拖拽时可以获取到被拖拽的对象属性定义 要使用 :clone, 而不是clone。我想应该是因为draggable标签比较特。另外在使用**:clone时要将…...

Vue 实例的数据对象详解
Vue 实例的数据对象详解 在 Vue 中,数据对象是响应式系统的核心,也是组件状态的载体。理解数据对象的原理和使用方式是成为 Vue 专家的关键一步。我将从多个维度深入剖析 Vue 实例的数据对象。 一、数据对象的定义方式 1. Options API 中的定义 在 Options API 中,使用 …...
