acwing3417. 砝码称重
acwing3417. 砝码称重
- 算法 1: DFS
- 算法2 : DP
算法 1: DFS
/*** 数据范围
对于 50%的评测用例,1≤N≤15.
对于所有评测用例,1≤N≤100,N 个砝码总重不超过 1e5.
*/
/*
算法 1: DFS
思路 : 对于每个砝码,有放在左边,放在右边,和不放三种选择,使用深搜来遍历所有可能情况,并记录出现过的重量
时间复杂度 : O(N^3)
空间复杂度 : O(N)
*/
#include <iostream>
#include <set>
using namespace std;const int N = 110;
int n ;
int w[N];
set<int> st;void dfs(int u ,int s)
{if(u == n){if(s>0)st.insert(s);return ;}dfs(u+1 , s+w[u]);dfs(u+1 , s-w[u]);dfs(u+1 , s);
}int main()
{cin >> n;for(int i = 0 ;i < n ;i ++)cin >> w[i];dfs(0 , 0);//遍历到第u个砝码,总重量为多少cout<<st.size()<<endl;return 0;
}
算法2 : DP
本题是一个典型的背包问题,我们可以用动态规划来解决。状态转移方程为f[i][j]f[i][j]f[i][j] 表示前 iii个砝码能否凑出重量 jjj,如果能够凑出,则 f[i][j]=truef[i][j]=truef[i][j]=true,否则 f[i][j]=falsef[i][j]=falsef[i][j]=false。
对于第 iii个砝码,它可以选择放在天平左边、右边或者不放,因此有以下三种情况:
不放第 iii 个砝码,则 f[i][j]=f[i−1][j];f[i][j]=f[i-1][j];f[i][j]=f[i−1][j];
将第 iii 个砝码放在天平左边,则 f[i][j]=f[i−1][j−W[i]];f[i][j]=f[i-1][j-W[i]];f[i][j]=f[i−1][j−W[i]];
将第 iii 个砝码放在天平右边,则f[i][j]=f[i−1][j+W[i]]f[i][j]=f[i-1][j+W[i]]f[i][j]=f[i−1][j+W[i]]。
综合上述三种情况,我们可以得到状态转移方程:
f[i][j]={f[i−1][j],f[i−1][j]or f[i−1][j−Wi]or f[i−1][j+Wi]f[i][j]= \begin{cases} f[i-1][j], \\ f[i-1][j] \text{or}\ f[i-1][j-W_i] \text{or}\ f[i-1][j+W_i] \end{cases} f[i][j]={f[i−1][j],f[i−1][j]or f[i−1][j−Wi]or f[i−1][j+Wi]
最终答案即为有多少个 f[N][j]f[N][j]f[N][j] 的值为 true。
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 110, M = 200010, B = M / 2;
/*
[-100000,100000]=>200010
*/int n, m;
int w[N];
bool f[N][M];int main()
{scanf("%d", &n);for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]), m += w[i];f[0][B] = true;for (int i = 1; i <= n; i ++ )for (int j = -m; j <= m; j ++ ){//状态转移方程:是否可以由"右状态"转移到"左状态"f[i][j + B] = f[i - 1][j + B];if (j - w[i] >= -m) f[i][j + B] |= f[i - 1][ j - w[i] + B ];//如果存在j - w[i] + B这样的重量,那么就可以从j - w[i] + B这个状态转移到j + B这个状态if (j + w[i] <= m) f[i][j + B] |= f[i - 1][ j + w[i] + B ];}int res = 0;for (int j = 1; j <= m; j ++ )if (f[n][j + B])res ++ ;printf("%d\n", res);return 0;
}相关文章:

acwing3417. 砝码称重
acwing3417. 砝码称重算法 1: DFS算法2 : DP算法 1: DFS /*** 数据范围 对于 50%的评测用例,1≤N≤15. 对于所有评测用例,1≤N≤100,N 个砝码总重不超过 1e5. */ /* 算法 1: DFS 思路 : 对于每个砝码,有放在左边,放在右边,和不放三种选择,使…...

生成式 AI:百度“文心一言”对标 ChatGPT?什么技术趋势促使 ChatGPT 火爆全网?
文章目录前言一、生成式 AI 的发展和现状1.1、什么是生成式 AI?1.2、生成式 AI 的发展趋势1.3、AI 生成内容的业务场景和分类二、生成式 AI 从分析领域到创作领域2.1、 降低内容创作门槛,增加 UGC 用户群体2.2、提升创作及反馈效率,铺垫线上实…...
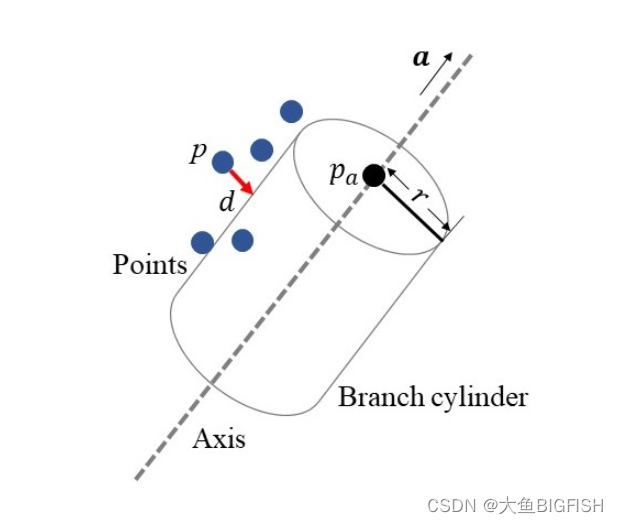
PCL 非线性最小二乘法拟合圆柱
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 这里通过非线性最小二乘的方法来实现圆柱体的拟合,具体的计算过程如下所述: 图中, p p p为输入数据的点位置,求解的参数为柱体的轴向向量 a...
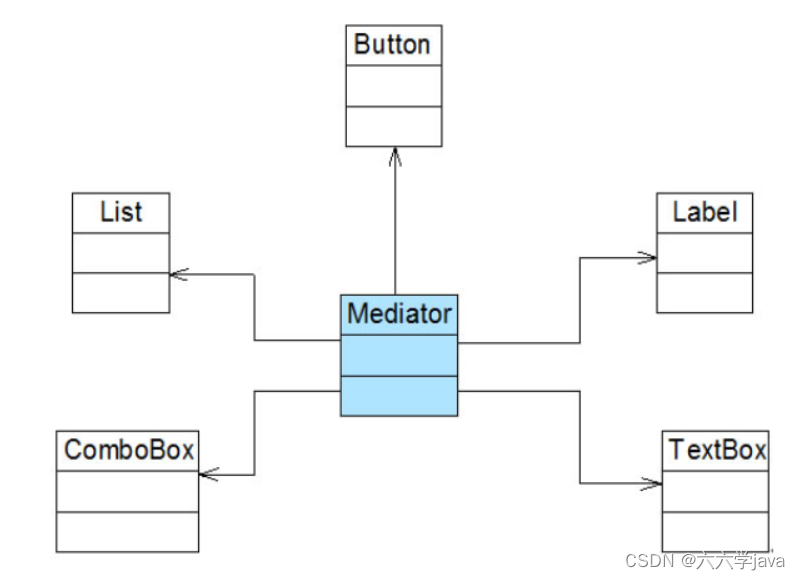
【设计模式】迪米特法则
文章目录一、迪米特法则定义二、迪米特法则分析三、迪米特法则实例一、迪米特法则定义 迪米特法则(Law of Demeter, LoD):一个软件实体应当尽可能少地与其他实体发生相互作用。 二、迪米特法则分析 如果一个系统符合迪米特法则,那么当其中某一个模块发…...

CSS3笔试题精讲1
Q1 BFC专题 防止父元素高度坍塌 4种方案 父元素的高度都是由内部未浮动子元素的高度撑起的。 如果子元素浮动起来,就不占用普通文档流的位置。父元素高度就会失去支撑,也称为高度坍塌。 即使有部分元素留在普通文档流布局中支撑着父元素,如果浮动 起来的元素高度高于留下的…...
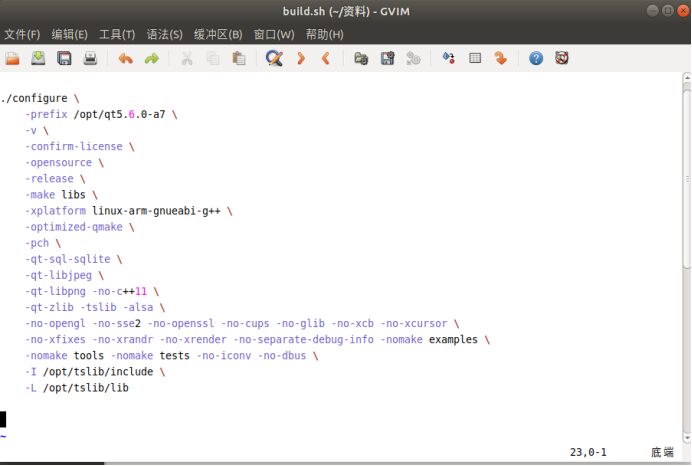
交叉编译用于移植的Qt库
前言 如果在Ubuntu上使用qt开发可移植到周立功开发板的应用程序,需要在Ubuntu上交叉编译用于移植的Qt库,具体做法如下: 1、下载源码 源码qt-everywhere-opensource-src-5.9.6.tar.xz拷贝到ubuntu自建的software文件下 2、解压 点击提取到此处 3、安装配置 运行脚本文…...

泰凌微TLSR8258 zigbee开发环境搭建
目录必备软件工具抓包分析辅助工具软件开发包PC 辅助控制软件 (ZGC)必备软件工具 下载地址:http://wiki.telink-semi.cn/ • 集成开发环境: TLSR8 Chips: Telink IDE for TC32 TLSR9 Chips: Telink RDS IDE for RISC-V • 下载调试工具: Telink Burning and Debugg…...

C#实现商品信息的显示异常处理
实验四:C#实现商品信息的显示异常处理 任务要求: 在进销存管理系统中,商品的库存信息有很多种类,比如商品型号、商品名称、商品库存量等。在面向对象编程中,这些商品的信息可以存储到属性中,然后当需要使…...
)
细数N个获取天气信息的免费 API ,附超多免费可用API 推荐(三)
前言 市面上有 N 多个查询天气信息的软件、小程序以及网页入口,基本都是通过调用天气查询 API 去实现的。 今天整理了一下多种场景的天气预报API 接口分享给大家,有需要赶紧收藏起来。 天气预报查询 天气预报查询支持全国以及全球多个城市的天气查询…...

20230404英语学习
今日单词 decade n.十年 allocate vt.分配,分派,把…拨给 compress v.压缩;缩短;浓缩 regenerate v.(使)复兴,(使)振兴;(使)再生 …...
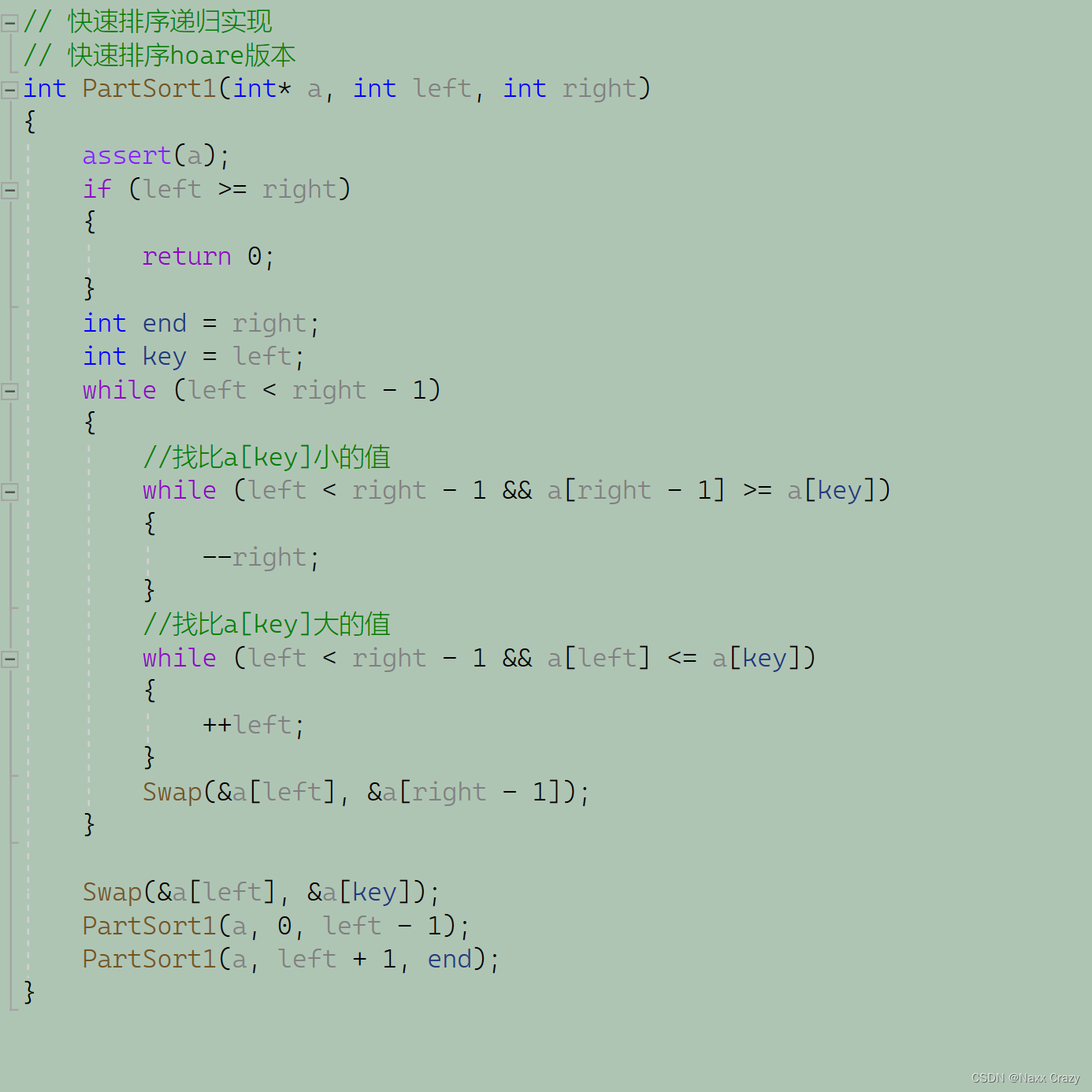
冒泡排序 快排(hoare递归)
今天要讲一个是冒泡排序,进一个是快排,首先是冒泡排序,我相信大家接触的第一个排序并且比较有用的算法就是冒泡排序了,冒泡排序是算法里面比较简单的一种,所以我们先看看一下冒泡排序 还是个前面一样,我们…...

49天精通Java,第24天,Java链表、散列表、HashSet、TreeSet
目录一、链表二、散列表三、HashSet四、TreeSet五、TreeSet常用方法大家好,我是哪吒。 一、链表 从数组中间删除一个元素开销很大,其原因是向数组中插入元素时,此元素之后的所有元素都要向后端移动,删除时也是,数组中…...

HashMap源码分析小结
HashMap相关问题 HashMap实现原理 HashMap是以键值对的形式存储数据,内部是通过数组链表结构实现,在1.7之后的版本,链表结构可以升级为红黑树,提高查询效率 key和value都支持为null;key为null时hash值是0࿰…...

太奇怪了!小公司面试全挂,大厂面试全过,为什么小公司要求比大厂还高?...
大厂的人才去小公司面试,一定是降维打击吗?还真未必。一位网友很困惑:真的奇怪,小公司面试全挂,大厂面试10个过了9个,感觉小公司要求比大厂还高,这是怎么了?来看看网友们的看法。有人…...

Java开发环境配置
Java开发环境配置 Java是目前世界上最流行的编程语言之一,它的使用范围广泛,从Web应用程序到桌面应用程序再到移动应用程序,Java都是一种非常有用的语言。想要进行Java开发,首先需要在计算机上配置Java开发环境。 在本文中&…...
大学英语视听说教程(陈向京版本)
词汇题(55道) 1. You should carefully think over_____ the manager said at the meeting. A. that B. which C. what D. whose 1.选C,考察宾语从句连接词,主句谓语动词think over后面缺宾语,后面的宾语从句谓语动…...

nginx--开源免费
nginx开源免费,支持高性能,高并发的web服务和代理服务软件。 apache,nodejs nginx可以提供的服务: 1、web服务 2、负载均衡(反向代理)(动静分离) 3、web cache(web缓存) nginx…...
阿里云OSS对象存储
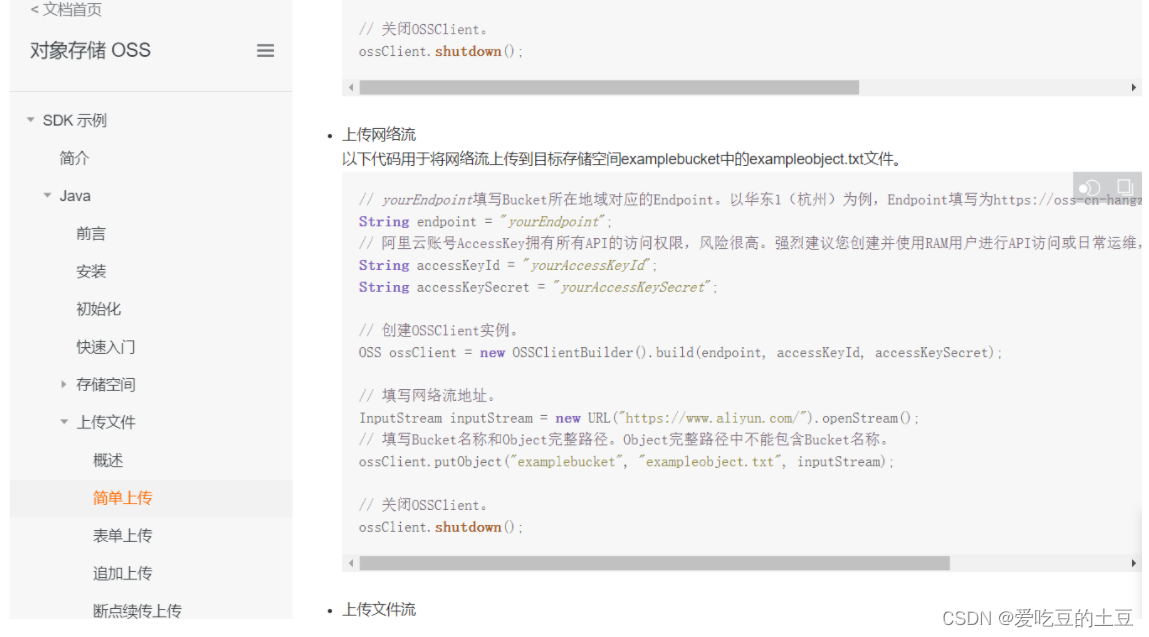
目录 1:OSS 1.1:开通OSS服务 1.2:搭建OSS环境 1.2.1:创建Bucket存储空间 1.2.2:创建文件夹上传图片 1.2.3:RAM访问控制 1.3:快速入门 1.3.1:下载SDK 1.3.2:搭建环…...
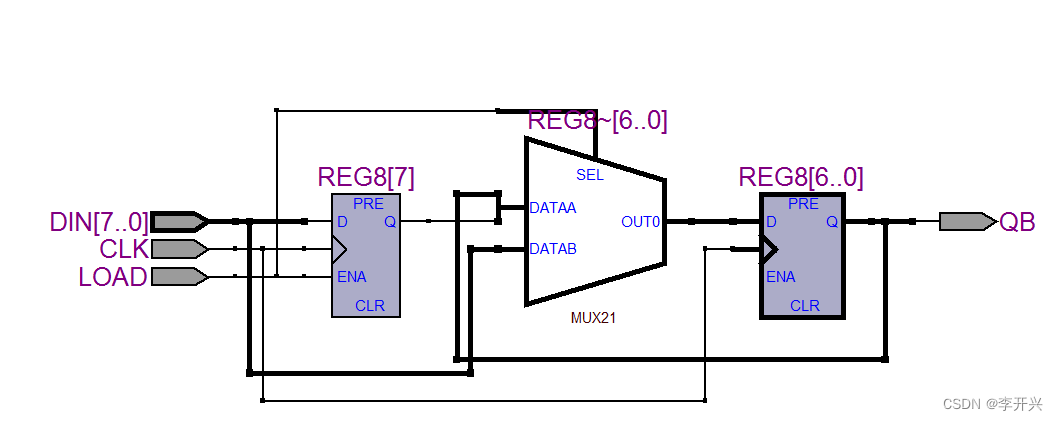
基于VHDL语言的汽车测速系统设计_kaic
摘 要 汽车是现代交通工具。车速是一项至关重要的指标。既影响着汽车运输的生产率,又关乎着汽车行驶有没有超速违章,还影响着汽车行驶时人们的人身安全。而伴随着我国国民的安全防范意识的逐步增强,人们也开始越来越关心因为汽车的超速而带来的极其严重…...

【数据结构】单链表(笔记总结)
👦个人主页:Weraphael ✍🏻作者简介:目前学习C和算法 ✈️专栏:数据结构 🐋 希望大家多多支持,咱一起进步!😁 如果文章对你有帮助的话 欢迎 评论💬 点赞&…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
