Python数据分析-Scipy科学计算法
1.认识Scipy
SciPy(发音为 "Sigh Pie")是一个开源的 Python 算法库和数学工具包。
通常与 NumPy、Matplotlib 和 pandas 等库一起使用,这些库共同构成了 Python 的科学计算基础。
2.使用Scipy基本函数
2.1 引用Scipy函数
import scipy.stats as st
2.2 构建一个简单的随机算数函数
2.2.1 引用函数、创建方程
衰减公式 : e = a * e^(-b*x)+c:
import numpy as np
import matplotlib.pyplot as plt
import scipy
def y(x,a,b,c):return a * np.exp(-b * x) + c2.2.2 构建数列
0~4之间的50个数:
xdata = np.linspace(0,4,50)
ydata = y(xdata,2.5,1.3,0.5)
print(xdata,ydata)2.2.3 模拟噪声处理
ydata_noise = ydata + 0.5 * np.random.randn(xdata.size)
plt.plot(xdata,ydata_noise)
#plt.show() 测试2.2.4 生成拟合曲线
params,pcov = scipy.optimize.curve_fit(y,xdata,ydata_noise)
plt.plot(xdata,y(xdata,*params))
plt.show()3. 随机变量与变量分布
创建一个具备正态分布形态的随机变量
s1 = st.norm.rvs(loc=0, scale=1, size=100):
生成了100个正态分布的随机数,并存储在变量 s1 中。其中随机数满足条件:
loc=0 期望值;scale=1 方差(标准差);size=100 数量
import seaborn as sns
import matplotlib.pyplot as plt
import scipy.stats as st
s1 = st.norm.rvs(loc=0,scale=1,size=100)
s2 = st.norm.rvs(loc=1,scale=2,size=100)
s3 = st.norm.rvs(loc=2,scale=3,size=100)
sns.distplot(s1)
sns.distplot(s2)
sns.distplot(s3)
plt.legend(labels=[1,2,3])
plt.show()
4.检测检验
4.1 分布图:总体VS样本
s0 = st.norm.rvs(72,1,1000)#测试总体概率
s1 = st.norm.rvs(68,0.8,100)#测试样本概率
sns.distplot(s0)
sns.distplot(s1)
plt.show()
4.2 置信区间、拒绝域
置信区间:总体概率为95%
拒绝域:概率p=5%=0.05,
>3*std:当类别数据>3个方差时,就是小概率事件,即,可以拒绝原假设,接收备择假设。
plt.figure(figsize=(10,5))#设置窗口尺寸
sns.distplot(st.norm.rvs(size=1000))
plt.show()
4.3 计算出现的频率
print(st.norm.cdf(-2))
print(st.norm.ppf(0.022))4.4 简单计算p值的方法
zscore = (68-72)/0.8
print(zscore)5. 流失vs非流失用户样本差异
5.1 数据预处理,提取月消费
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import scipy.stats as stdate = pd.read_csv('WA_Fn-UseC_-Telco-Customer-Churn.csv')
#按是否流失,提取月消费数据
churn0 = date[date['是否流失']=='No']['月消费']
churn1 = date[date['是否流失']=='Yes']['月消费']
print(churn0.head())5.2 观察分布结构
5.2.1 频数分布
plt.figure(figsize=(15,5))
churn0.hist(bins=50)
churn1.hist(bins=50)
plt.legend(labels=['churn0','churn1'])
plt.show()
5.2.2 概率分布
plt.figure(figsize=(15,5))
sns.distplot(churn0.tolist())
sns.distplot(churn1.tolist())
plt.legend(labels=['churn0','churn1'])
plt.show()
5.2.3 双侧检查:
是否存在显著性差异
H0:非流失用户μ值 = 流失用户μ值 ---均值无显著性差异
H1:非流失用户μ值 ≠ 流失用户μ值 ---均值有显著性差异
5.2.3.1 :st.ks_2samp(s0, s1)
这个函数执行Kolmogorov-Smirnov测试,用于比较两个样本是否来自同一分布。
s0 = churn0.tolist()
s1 = churn1.tolist()
print(st.ks_2samp(s0, s1))- statistic=0.24859894401422267, 统计量,值越小分布越相似
- pvalue=4.827359624586335e-75, 远远小于p值标准值0.05,拒绝H0接收H1
- statistic_location=68.8, 统计量位置,检验统计量发生位置
- statistic_sign=1 统计量符号 statistic_sign=1为正数
5.2.3.2 :st.describe(s0/s1)
这个函数输出样本s1/s0的描述性统计信息
print(st.describe(s0))
print(st.describe(s1))- nobs=5174, 数量
- minmax=(18.25, 118.75), 最大最小值
- mean=61.26512369540008, 均值
- variance=966.7527670734265,方差值
- skewness=-0.025012288702718842, 偏度值
- kurtosis=-1.3551511690013145)峰值
偏度值:统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征
峰值:概率密度分布曲线在平均值处峰值高低的特征数,如果峰度大于三,峰的形状比较尖
相关文章:

Python数据分析-Scipy科学计算法
1.认识Scipy SciPy(发音为 "Sigh Pie")是一个开源的 Python 算法库和数学工具包。 通常与 NumPy、Matplotlib 和 pandas 等库一起使用,这些库共同构成了 Python 的科学计算基础。 2.使用Scipy基本函数 2.1 引用Scipy函数 impor…...

【Python Django + Vue】酒店在线预订系统:用技术说话!
🎓 作者:计算机毕设小月哥 | 软件开发专家 🖥️ 简介:8年计算机软件程序开发经验。精通Java、Python、微信小程序、安卓、大数据、PHP、.NET|C#、Golang等技术栈。 🛠️ 专业服务 🛠️ 需求定制化开发源码提…...

禁用微软的windos安全中心
目录 一、为什么禁用 二、WDControl_1.5.0程序禁用windows安全中心 步骤1--- 步骤2--- 三、禁用widows安全中心成功 一、为什么禁用 描述:下载第三方软件常常会收到病毒防护秒杀, 第1---直接无法下载 第2---提前下载在U盘解压会被干掉程序文件 …...

2.html编辑器介绍
html编辑器介绍 HTML 编辑器推荐 理论上我们可以使用记事本进行html编码和开发,但是在实际开发html页面的时候,使用一些专业的开发工具可以使我们更加快速和高效的进行开发,下面介绍几种开发工具: VS Code:https://…...

树莓派应用--AI项目实战篇来啦-17.YOLOv8目标检测-安全帽检测
1. YOLOv8介绍 YOLOv8是Ultralytics公司2023年推出的Yolo系列目标检测算法,可以用于图像分类、物体检测和实例分割等任务。YOLOv8作为YOLO系列算法的最新成员,在损失函数、Anchor机制、样本分配策略等方面进行了全面优化和创新。这些改进不仅提高了模型的…...

git-secret介绍
git-secret介绍 git-secret 是一个与git兼容的命令行工具,旨在安全地存储和管理敏感数据,如源代码中的密码、密钥以及敏感文件。它通过 GPG 加密来保护文件,确保只有授权的用户才能访问这些敏感信息。 使用流程 1、安装 Git-Secret:在本地开发环境中安装 git-secret。 2…...

【实战】Nginx+Lua脚本+Redis 实现自动封禁访问频率过高IP
大家好,我是冰河~~ 自己搭建的网站刚上线,短信接口就被一直攻击,并且攻击者不停变换IP,导致阿里云短信平台上的短信被恶意刷取了几千条,加上最近工作比较忙,就直接在OpenResty上对短信接口做了一些限制&am…...
计算机专业大一课程:线性代数探秘
计算机专业大一课程:线性代数探秘 对于计算机专业的大一新生来说,线性代数是一门基础且重要的课程。它不仅是数学的一个分支,更是计算机科学中不可或缺的工具。那么,线性代数究竟包含哪些内容,对我们的计算机学习有何…...

vscode写markdown插入图片视频并放在指定目录
目录 前言正文 前言 各种云文档非常好用,但是当你想把这些资料保存在本地时,markdown我觉得是最好的选择 markdown编辑器也有很多,但我还是觉得vscode最好用,直接粘贴文件就可以插入也类似云文档的使用体验,但是想要…...

鸿蒙富文本显示
1.使用 RichText 组件(ArkTS) 背景知识:在 ArkTS(一种鸿蒙应用开发语言)中,RichText组件提供了更强大的富文本显示功能。它允许设置不同的文本样式,包括字体、颜色、字号等多种属性。 Rich Te…...

手写mybatis之细化XML语句构建器,完善静态SQL解析
前言 1:在流程上,通过 DefaultSqlSession#selectOne 方法调用执行器,并通过预处理语句处理器 PreparedStatementHandler 执行参数设置和结果查询。 2:那么这个流程中我们所处理的参数信息,也就是每个 SQL 执行时&#…...

使用Milvus和Llama-agents构建更强大的Agent系统
代理(Agent)系统能够帮助开发人员创建智能的自主系统,因此变得越来越流行。大语言模型(LLM)能够遵循各种指令,是管理 Agent 的理想选择,在许多场景中帮助我们尽可能减少人工干预、处理更多复杂任…...

Python 工具库每日推荐【Arrow】
文章目录 引言Python时间日期处理库的重要性今日推荐:Arrow工具库主要功能:使用场景:安装与配置快速上手示例代码代码解释实际应用案例案例:跨时区会议安排器案例分析高级特性时间范围和区间自定义时间格式扩展阅读与资源优缺点分析优点:缺点:总结【 已更新完 TypeScript…...

Win10 安装 Redis 数据库
一、Redis 数据库介绍 Redis 是一个开源的高性能键值对(key-value)的非关系型数据库。它通常用作数据结构服务器,支持多种类型的数据结构,如字符串(strings)、哈希(hashes)、列表&a…...

使用springboot生成war包
1.生成war包 1.1 更改pom包 打开一个springboot 项目 ,右击项目名从项目管理器打开 在pom.xml文件中插入以下两个依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-devtools</artifactId><…...

见微知著:OpenEuler系统启动流程
OpenEuler是一个开源的Linux发行版,它的启动流程涉及到多个阶段,包括固件初始化、引导加载程序、内核启动、初始化系统和服务管理器等。下面将详细介绍OpenEuler的启动流程。 一、启动流程 1. 固件初始化(BIOS/UEFI) 启动过程首…...

支持向量机-笔记
支持向量机(Support Vector Machine, SVM) 是一种强大的监督学习算法,广泛应用于分类和回归任务,特别是在分类问题中表现优异。SVM 的核心思想是通过寻找一个最优超平面,将不同类别的数据点进行分割,并最大…...
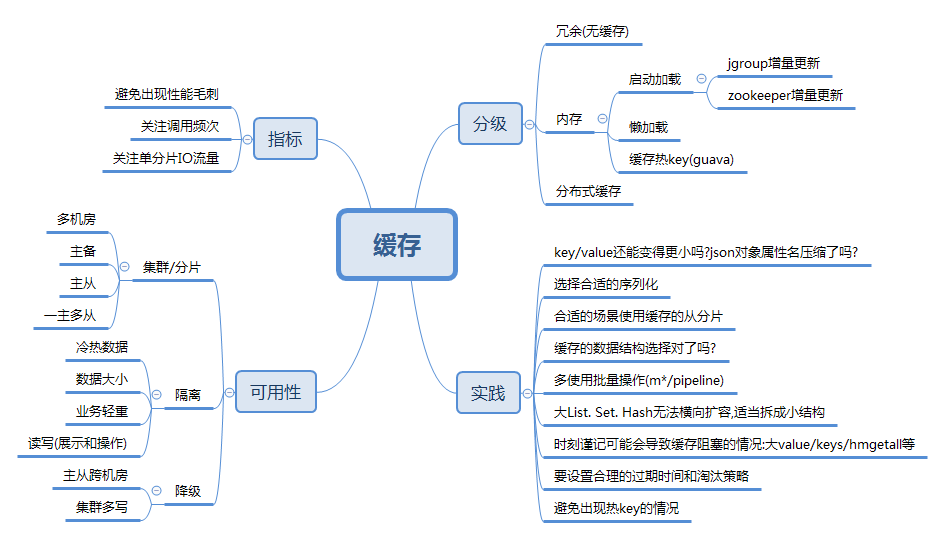
研发线上事故风险解读之缓存篇
专业在线打字练习平台-巧手打字通,只输出有价值的知识。 一 前言 本文继续基于《线上事故案例集》,进一步深入梳理线上事故缓存使用方面的问题点,重点关注缓存在使用和优化过程中可能出现的问题,旨在为读者提供具有实践指导意义的…...

JavaScript前端开发技术
JavaScript前端开发技术 引言 JavaScript(简称JS)是一种广泛使用的脚本语言,特别在前端开发领域,它几乎成为了网页开发的标配。从简单的表单验证到复杂的单页应用(SPA),JavaScript都扮演着不可…...

H.264 编码参数优化策略
一、概述 随着数字媒体技术的发展,视频编码成为了多媒体领域中的重要研究方向之一。而H.264作为一种广泛应用的视频编码标准,具有高压缩比、优质画面和广泛兼容性等优点。为了进一步提高视频质量和压缩效率,对H.264编码参数进行优化成为了一个…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
