支持向量机-笔记
支持向量机(Support Vector Machine, SVM) 是一种强大的监督学习算法,广泛应用于分类和回归任务,特别是在分类问题中表现优异。SVM 的核心思想是通过寻找一个最优超平面,将不同类别的数据点进行分割,并最大化两类数据之间的间隔(即“边距”)。SVM 的本质是一个二分类算法,但它也可以扩展到多分类和回归问题。
大白话:例如在二维中进行二分类,找一条直线把两类数据分开,且这条直线距离正负两类最近的点的距离最远,这个直线(二维)称为超平面,最近的点称为支持向量,超平面是由支持向量支撑起来的,软间隔则是允许忽略一些噪声数据点,由参数C决定忽略的力度。

1. 支持向量机的基本概念
超平面(Hyperplane)
超平面是指将数据空间划分为不同区域的一个线性决策边界。在二维空间中,超平面是一个线,而在三维空间中,超平面是一个平面。在n维空间中,超平面可以被认为是n-1维的平面。
支持向量(Support Vectors)
支持向量是指位于分类间隔边界上的数据点,这些点对超平面的最终位置有决定性的影响。SVM 寻找的最优超平面是由这些支持向量决定的。
边距(Margin)
边距是指两个类别之间的最小距离,SVM 的目标是最大化边距,即让两类数据之间的空隙尽可能大,以减少模型的误差和提高泛化能力。
- 硬间隔(Hard Margin)SVM:不允许分类错误,要求所有数据点都被完全正确分类。这种方法适合线性可分的数据。
- 软间隔(Soft Margin)SVM:允许一些数据点在决策边界的错误一侧,以便处理有噪声或线性不可分的数据。

2. 支持向量机的数学原理
线性可分 SVM
假设我们有一个线性可分的二分类数据集,SVM 的目标是找到一个最优的超平面,使得超平面两侧的分类边距最大化。
-
超平面的方程:
![]()
其中,w 是法向量,决定超平面的方向,b是偏置。
2.决策函数:
![]()
决策函数用于预测数据点属于哪个类别,输出结果为1或-1。
3.优化目标: 为了最大化分类边距,SVM 需要最小化 w 的范数,同时满足数据点的分类条件:
![]()
其中 yi为第 i个样本的标签(1或-1)。
最终优化问题可以表示为:
![]()
约束条件为:
![]()
软间隔 SVM
对于线性不可分的数据,SVM 引入了松弛变量(Slack Variables) ξi,允许一些数据点违背分类规则。优化问题变为:

约束条件为:
![]()
其中,C 是一个超参数,控制模型的柔韧性,允许一些分类错误以便更好地处理线性不可分数据。
3. 核方法(Kernel Trick)
当数据在原始特征空间中线性不可分时,SVM 使用核方法将数据映射到高维空间,使得在高维空间中线性可分。常见的核函数有:
大白话:当前维度不可分,则将数据映射到高维。

-
线性核(Linear Kernel)
![]()
适用于线性可分的数据。
2.多项式核(Polynomial Kernel)
![]()
其中 c 是常数,d 是多项式的次数,适用于具有多项式关系的数据。
3.径向基函数核(Radial Basis Function, RBF Kernel)
![]()
RBF 核非常适用于处理非线性数据,且在实际应用中非常常见。
4.Sigmoid核(Sigmoid Kernel)
![]()
这个核函数与神经网络中的激活函数相关联。
4. 支持向量机的优缺点
优点:
- 高效的处理高维数据:SVM 在处理高维空间的数据时表现出色,尤其是在维度高于样本数的情况下。
- 内存高效:SVM 只利用支持向量来构建决策边界,因此它并不需要整个数据集。
- 灵活性强:通过核方法,SVM 能够处理线性不可分的数据。
- 鲁棒性强:SVM 能够很好地处理噪声数据,并且可以通过调整软间隔参数 C 来控制过拟合。
缺点:
- 训练时间较长:特别是在样本数很大时,SVM 的训练时间会显著增加,因为计算复杂度较高。
- 难以处理多分类问题:SVM 本质上是二分类算法,尽管可以通过“一对一”或“一对多”的方法扩展到多分类任务,但实现较为复杂。
- 参数调优复杂:SVM 需要调节多个参数(如核函数、软间隔参数 C、核的超参数等),找到最优参数组合需要大量调试。
- 难以处理大规模数据:SVM 对大规模数据的处理效率较低。
5. SVM的调参要点
SVM 的性能在很大程度上取决于参数的选择,以下是常用的超参数及其调优策略:
-
核函数选择:核函数选择是最重要的参数之一,不同的核函数适用于不同类型的数据。线性数据可以选择线性核,非线性数据则使用 RBF 核或多项式核。
-
软间隔参数 C:该参数控制模型对误分类的容忍度。C 值越大,模型越倾向于对训练数据进行严格分类,可能导致过拟合;C 值越小,模型对误分类的容忍度越高,可能导致欠拟合。
-
核参数 γ:对于 RBF 核函数,γ控制单个样本的影响范围。较小的 γ值会使模型较为平滑,较大的 γ值会让模型更加拟合训练数据。
-
交叉验证:使用网格搜索(Grid Search)和交叉验证(Cross-Validation)可以帮助找到最优的 C 和 γ参数组合。
6. SVM 的 Python 实现示例
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score# 加载数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target# 分割训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 定义支持向量机模型(使用RBF核)
svm_model = SVC(kernel='rbf', C=1, gamma=0.1)# 训练模型
svm_model.fit(X_train, y_train)# 进行预测
y_pred = svm_model.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.2f}')
7. 常见面试问题
-
什么是支持向量机?
- 回答要点:SVM 是一种监督学习算法,寻找最优超平面来最大化分类间隔。
-
什么是支持向量?
- 回答要点:支持向量是位于决策边界附近的数据点,它们对超平面的位置有决定性作用。
-
解释SVM中的软间隔和硬间隔的区别。
- 回答要点:硬间隔不允许分类错误,适用于线性可分数据;软间隔允许部分误分类,适用于线性不可分数据。
-
什么是核方法?为什么需要核方法?
- 回答要点:核方法用于将数据映射到高维空间,使得在高维空间中线性可分,从而找到最优超平面。
-
如何选择SVM的参数 C 和 γ?
- 回答要点:通过交叉验证和网格搜索找到最优的参数,C 控制误分类的惩罚,γ 控制核函数的影响范围。
相关文章:

支持向量机-笔记
支持向量机(Support Vector Machine, SVM) 是一种强大的监督学习算法,广泛应用于分类和回归任务,特别是在分类问题中表现优异。SVM 的核心思想是通过寻找一个最优超平面,将不同类别的数据点进行分割,并最大…...
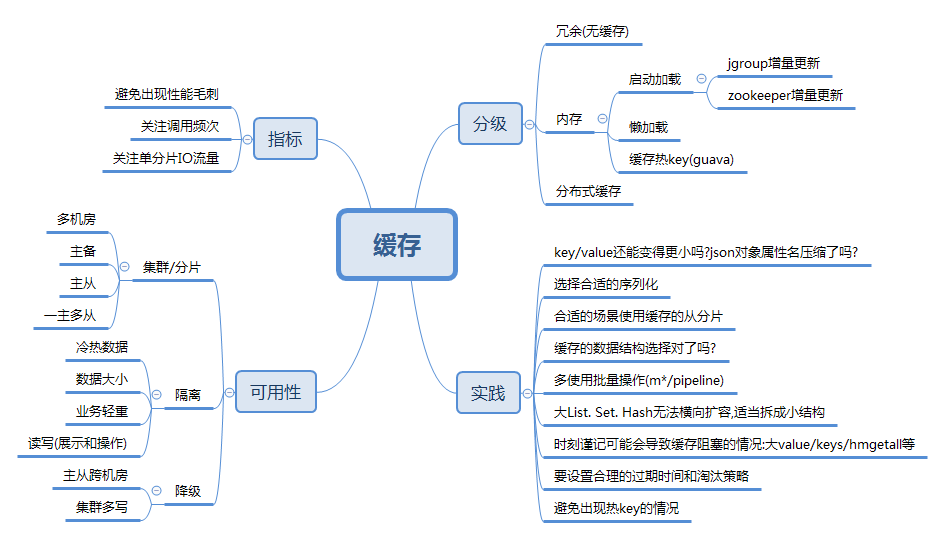
研发线上事故风险解读之缓存篇
专业在线打字练习平台-巧手打字通,只输出有价值的知识。 一 前言 本文继续基于《线上事故案例集》,进一步深入梳理线上事故缓存使用方面的问题点,重点关注缓存在使用和优化过程中可能出现的问题,旨在为读者提供具有实践指导意义的…...

JavaScript前端开发技术
JavaScript前端开发技术 引言 JavaScript(简称JS)是一种广泛使用的脚本语言,特别在前端开发领域,它几乎成为了网页开发的标配。从简单的表单验证到复杂的单页应用(SPA),JavaScript都扮演着不可…...

H.264 编码参数优化策略
一、概述 随着数字媒体技术的发展,视频编码成为了多媒体领域中的重要研究方向之一。而H.264作为一种广泛应用的视频编码标准,具有高压缩比、优质画面和广泛兼容性等优点。为了进一步提高视频质量和压缩效率,对H.264编码参数进行优化成为了一个…...

C++ 游戏开发技术选型指南
C 游戏开发技术选型指南 游戏开发是一个复杂而多元化的领域,而C凭借其高性能和强大的控制能力,成为许多游戏引擎的首选编程语言。在这篇博客中,我们将探讨如何选择合适的C技术栈进行游戏开发,包括技术背景、代码示例、优化实践、…...

基于Python Django的在线考试管理系统
🍊作者:计算机毕设匠心工作室 🍊简介:毕业后就一直专业从事计算机软件程序开发,至今也有8年工作经验。擅长Java、Python、微信小程序、安卓、大数据、PHP、.NET|C#、Golang等。 擅长:按照需求定制化开发项目…...

《Java基础》变量和数据类型
综述 在开始学习变量之前,我们思考一下为什么需要使用变量。 首先我们从小开始学习加法减法的时候,后来我们再学更难的东西就是代数,其中的x和y是我们要求解的内容,这些内容就是变量。 变量是人的思维的提升,没有变量…...

FLINK内存管理解析,taskmanager、jobmanager
1、在 Flink 中设置内存的方法是配置以下两个选项之一: 1)Total Flink memory:taskmanager.memory.flink.sizejobmanager.memory.flink.size 2)Total process memory:taskmanager.memory.process.sizejobmanager.mem…...

【AI论文精读13】RAG论文综述2(微软亚研院 2409)P5-可解释推理查询L3
AI知识点总结:【AI知识点】 AI论文精读、项目、思考:【AI修炼之路】 P1,P2,P3,P4 五、可解释推理查询(L3) ps:P2有四种查询(L1,L2,L3,…...

优达学城 Generative AI 课程3:Computer Vision and Generative AI
文章目录 1 官方课程内容自述第 1 课:图像生成简介第 2 课:计算机视觉基础第 3 课:图像生成与生成对抗网络(GANs)第 4 课:基于 Transformer 的计算机视觉模型第 5 课:扩散模型第 6 课࿰…...

UE5 C++ 通过绑定编辑器事件实现控制柄顶点编辑
开发中经常会遇到编辑器环境中制作工具拖拽控制柄编辑内容的需求,此时可以通过Editor事件拿到对应回调,进行相应更新: 1.创建Mesh编辑Actor类 创建一个Mesh编辑Actor类,提供Mesh顶点编辑的相关逻辑。 .h: #pragma once#inclu…...

云计算ftp 服务器实验
创建VLAN 10 划分端口 创建VLAN 10 的地址 10.1.1.1 服务器的地址是 10.1.1.2 这是服务上的配置 服务器上选择ftp 启动 ,文件目录选择一下 在 交换机上 ftp 10.1.1.2 服务器的地址 把刚才创建的shenyq txt 文件下载下到本地交换机 我们能看到交换…...

node.js服务器基础
node.js的事件循环 node.js是基于事件驱动的,通常在代码中注册想要等待的事件,设定好回调函数,当事件触发的时候就会调用回调函数。如果node.js没有要处理的事件了,那整个就结束了;事件里面可以继续插入事件,如果有事…...

2-SAT 问题详解:逻辑约束与图论的结合
2-SAT 问题详解:逻辑约束与图论的结合 2-SAT(Two Satisfiability Problem)是布尔可满足性问题(SAT)的特殊形式,它解决的是含有二元子句的布尔表达式的可满足性问题。2-SAT 问题常用于分析系统中的逻辑约束…...

使用NetTopologySuite读写gpkg文件
直接上代码: 优势是什么?纯C#开发,不存在兼容和字符问题。 using NetTopologySuite; using NetTopologySuite.Features; using NetTopologySuite.Geometries; using CdIts.NetTopologySuite.IO; using CdIts.NetTopologySuite.IO.GeoPackag…...

什么是http?列出常见方法并解他们?
HTTP 方法是客户端(通常是浏览器)用来向服务器表明其意图的方式。常见的 HTTP 方法有以下几种: 一、GET 解释:用于请求指定的资源。它是最常见的 HTTP 方法之一。GET 方法应该只用于获取数据,而不应该有任何副作用。例…...
)
通过修改注册表来提高导出图像的分辨率(PPT尝试)
通过修改注册表来提高 PowerPoint 导出图片的分辨率,可以导致导出的图片尺寸大于您期望的 1920 x 1080 像素。例如,将 ExportBitmapResolution 设置为 300 DPI,可能会导致输出图像的尺寸变得非常大,比如 10240 x 5760 像素。这是因…...

OpenCV 环境配置
首先下载opencv,在opencv官网进行下载。 按照上面的步骤,点击进去 滑至底部,不切换至不同页,选择合适的版本进行下载(Window系统选择Windows版本进行下载)。 接下来以4.1.2版本为例: 点击之后会进入这个页面ÿ…...

使用通义千问模拟ChatGPT-o1进行思考,并以类似于ChatGPT-o1的形式输出
prompt 你是ChatGPT O1,旨在通过第一性原理思维和基于证据的推理来解决用户问题。你的目标是提供清晰、循序渐进的解决方案、基础概念,并从头开始构建答案。 ### 指导原则: 以下是为大模型采用这种方法而设计的系统提示: 1. 理解…...

维生素对于生活的重要性
在探索健康奥秘的旅途中,维生素作为人体不可或缺的微量营养素,扮演着至关重要的角色。它们虽不直接提供能量,却是酶促反应、细胞代谢、免疫功能乃至心理健康的基石。今天,让我们一同深入探讨人体所需补充的维生素,这些…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...
