初知C++:AVL树
文章目录
- 初知C++:AVL树
- 1.AVL树的概念
- 2.AVL树的是实现
- 2.1.AVL树的结构
- 2.2.AVL树的插入
- 2.3.旋转
- 2.4.AVL树的查找
- 2.5.AVL树平衡检测

初知C++:AVL树
1.AVL树的概念
• AVL树是最先发明的自平衡⼆叉查找树,AVL是⼀颗空树,或者具备下列性质的⼆叉搜索树:它的左右子树都是AV树,且左右子树的高度差的绝对值不超过1。AVL树是⼀颗高度平衡搜索⼆叉树,通过控制⾼度差去控制平衡。
• AVL树得名于它的发明者G.M.Adelson-Velsky和E.M.Landis是两个前苏联的科学家,他们在1962年的论⽂《Analgorithmfortheorganizationofinformation》中发表了它。
• AVL树实现这⾥我们引⼊⼀个平衡因⼦(balancefactor)的概念,每个结点都有⼀个平衡因⼦,任何结点的平衡因⼦等于右⼦树的⾼度减去左⼦树的⾼度,也就是说任何结点的平衡因⼦等于0/1/-1,AVL树并不是必须要平衡因⼦,但是有了平衡因⼦可以更⽅便我们去进⾏观察和控制树是否平衡,就像⼀个⻛向标⼀样。
• 思考⼀下为什么AVL树是⾼度平衡搜索⼆叉树,要求⾼度差不超过1,⽽不是⾼度差是0呢?0不是更好的平衡吗?画画图分析我们发现,不是不想这样设计,⽽是有些情况是做不到⾼度差是0的。⽐如⼀棵树是2个结点,4个结点等情况下,⾼度差最好就是1,⽆法作为⾼度差是0 。
• AVL树整体结点数量和分布和完全⼆叉树类似,⾼度可以控制在 logN,那么增删查改的效率也可以控制在O(logN),相⽐⼆叉搜索树有了本质的提升。
2.AVL树的是实现
2.1.AVL树的结构
在下图我们可以看到_parent指针,后续更新平衡因子,有很大的作用。

2.2.AVL树的插入
2.2.1 AVL树插⼊⼀个值的⼤概过程
-
插⼊⼀个值按⼆叉搜索树规则进⾏插⼊。
-
新增结点以后,只会影响祖先结点的⾼度,也就是可能会影响部分祖先结点的平衡因⼦,所以更新
从新增结点->根结点路径上的平衡因⼦,实际中最坏情况下要更新到根,有些情况更新到中间就可
以停⽌了,具体情况我们下⾯再详细分析。 -
更新平衡因⼦过程中没有出现问题,则插⼊结束
-
更新平衡因⼦过程中出现不平衡,对不平衡⼦树旋转,旋转后本质调平衡的同时,本质降低了⼦树
的⾼度,不会再影响上⼀层,所以插⼊结束。
2.2.2 平衡因⼦更新
更新原则:
•
平衡因⼦=右⼦树⾼度-左⼦树⾼度(也可以变为左子树的高度-右子树的高度)
•
只有⼦树⾼度变化才会影响当前结点平衡因⼦。
•
插⼊结点,会增加⾼度,所以新增结点在parent的右⼦树,parent的平衡因⼦++,新增结点在
parent的左⼦树,parent平衡因⼦–
•
parent所在⼦树的⾼度是否变化决定了是否会继续往上更新
更新停⽌条件:
•
更新后parent的平衡因⼦等于0,更新中parent的平衡因⼦变化为-1->0或者1->0,说明更新前
parent⼦树⼀边⾼⼀边低,新增的结点插⼊在低的那边,插⼊后parent所在的⼦树⾼度不变,不会
影响parent的⽗亲结点的平衡因⼦,更新结束。
•
更新后parent的平衡因⼦等于1或-1,更新前更新中parent的平衡因⼦变化为0->1或者0->-1,说
明更新前parent⼦树两边⼀样⾼,新增的插⼊结点后,parent所在的⼦树⼀边⾼⼀边低,parent所
在的⼦树符合平衡要求,但是⾼度增加了1,会影响arent的⽗亲结点的平衡因⼦,所以要继续向上
更新。
•
更新后parent的平衡因⼦等于2或-2,更新前更新中parent的平衡因⼦变化为1->2或者-1->-2,说
明更新前parent⼦树⼀边⾼⼀边低,新增的插⼊结点在⾼的那边,parent所在的⼦树⾼的那边更⾼
了,破坏了平衡,parent所在的⼦树不符合平衡要求,需要旋转处理,旋转的⽬标有两个:1、把
parent⼦树旋转平衡。2、降低parent⼦树的⾼度,恢复到插⼊结点以前的⾼度。所以旋转后也不
需要继续往上更新,插⼊结束。
更新到10结点,平衡因⼦为2,10所在的⼦树已经不平衡,需要旋转处理

更新到中间结点,3为根的⼦树⾼度不变,不会影响上⼀层,更新结束

最坏更新到根停⽌

2.2.3插⼊结点及更新平衡因⼦的代码实现



2.3.旋转
2.3.1 旋转的原则
- 保持搜索树的规则
- 让旋转的树从不满⾜变平衡,其次降低旋转树的⾼度
旋转总共分为四种,左单旋/右单旋/左右双旋/右左双旋。
说明:下⾯的图中,有些结点我们给的是具体值,如10和5等结点,这⾥是为了⽅便讲解,实际中是什
么值都可以,只要⼤⼩关系符合搜索树的规则即可。
2.3.2 右单旋
•
本图1展⽰的是10为根的树,有a/b/c抽象为三棵⾼度为h的⼦树(h>=0),a/b/c均符合AVL树的要
求。10可能是整棵树的根,也可能是⼀个整棵树中局部的⼦树的根。这⾥a/b/c是⾼度为h的⼦树,
是⼀种概括抽象表⽰,他代表了所有右单旋的场景,实际右单旋形态有很多种,具体图2/图3/图4/
图5进⾏了详细描述。
•
在a⼦树中插⼊⼀个新结点,导致a⼦树的⾼度从h变成h+1,不断向上更新平衡因⼦,导致10的平
衡因⼦从-1变成-2,10为根的树左右⾼度差超过1,违反平衡规则。10为根的树左边太⾼了,需要
往右边旋转,控制两棵树的平衡。
•
旋转核⼼步骤,因为5<b⼦树的值<10,将b变成10的左⼦树,10变成5的右⼦树,5变成这棵树新
的根,符合搜索树的规则,控制了平衡,同时这棵的⾼度恢复到了插⼊之前的h+2,符合旋转原
则。如果插⼊之前10整棵树的⼀个局部⼦树,旋转后不会再影响上⼀层,插⼊结束了。
下面五张图分别为右旋的各种情况!!!!!(请仔细观看有利于理解哦)
图1:

图2:

图3:

图4:

图5:

2.3.3 右单旋代码实现
这里传过去的parent是平衡因子为2或者-2的节点!
2.3.4左单旋
•本图6展⽰的是10为根的树,有a/b/c抽象为三棵⾼度为h的⼦树(h>=0),a/b/c均符合AVL树的要求。10可能是整棵树的根,也可能是⼀个整棵树中局部的⼦树的根。这⾥a/b/c是⾼度为h的⼦树,是⼀种概括抽象表⽰,他代表了所有右单旋的场景,实际右单旋形态有很多种,具体跟上⾯左旋类似。
•在a⼦树中插⼊⼀个新结点,导致a⼦树的⾼度从h变成h+1,不断向上更新平衡因⼦,导致10的平衡因⼦从1变成2,10为根的树左右⾼度差超过1,违反平衡规则。10为根的树右边太⾼了,需要往左边旋转,控制两棵树的平衡。
•旋转核⼼步骤,因为10<b⼦树的值<15,将b变成10的右⼦树,10变成15的左⼦树,15变成这棵树新的根,符合搜索树的规则,控制了平衡,同时这棵的⾼度恢复到了插⼊之前的h+2,符合旋转原则。如果插⼊之前10整棵树的⼀个局部⼦树,旋转后不会再影响上⼀层,插⼊结束了。

2.3.5左单旋代码实现

2.3.6左右双旋
通过图7和图8可以看到,左边⾼时,如果插⼊位置不是在a⼦树,⽽是插⼊在b⼦树,b⼦树⾼度从h变成h+1,引发旋转,右单旋⽆法解决问题,右单旋后,我们的树依旧不平衡。右单旋解决的纯粹的左边⾼,但是插⼊在b⼦树中,10为跟的⼦树不再是单纯的左边⾼,对于10是左边⾼,但是对于5是右边⾼,需要⽤两次旋转才能解决,以5为旋转点进⾏⼀个左单旋,以10为旋转点进⾏⼀个右单旋,这棵树这棵树就平衡了。
图7:

图8:

• 图7和图8分别为左右双旋中h0和h1具体场景分析,下⾯我们将a/b/c⼦树抽象为⾼度h的AVL⼦树进⾏分析,另外我们需要把b⼦树的细节进⼀步展开为8和左⼦树⾼度为h-1的e和f⼦树,因为我们要对b的⽗亲5为旋转点进⾏左单旋,左单旋需要动b树中的左⼦树。b⼦树中新增结点的位置不同,平衡因⼦更新的细节也不同,通过观察8的平衡因⼦不同,这⾥我们要分三个场景讨论。
• 场景1:h>=1时,新增结点插⼊在e⼦树,e⼦树⾼度从h-1并为h并不断更新8->5->10平衡因⼦,引发旋转,其中8的平衡因⼦为-1,旋转后8和5平衡因⼦为0,10平衡因⼦为1。
• 场景2:h>=1时,新增结点插⼊在f⼦树,f⼦树⾼度从h-1变为h并不断更新8->5->10平衡因⼦,引发旋转,其中8的平衡因⼦为1,旋转后8和10平衡因⼦为0,5平衡因⼦为-1。
• 场景3:h==0时,a/b/c都是空树,b⾃⼰就是⼀个新增结点,不断更新5->10平衡因⼦,引发旋转,其中8的平衡因⼦为0,旋转后8和10和5平衡因⼦均为0。

2.3.7 左右双旋代码实现

2.3.8右左双旋
•跟左右双旋类似,下⾯我们将a/b/c⼦树抽象为⾼度h的AVL⼦树进⾏分析,另外我们需要把b⼦树的细节进⼀步展开为12和左⼦树⾼度为h-1的e和f⼦树,因为我们要对b的⽗亲15为旋转点进⾏右单旋,右单旋需要动b树中的右⼦树。b⼦树中新增结点的位置不同,平衡因⼦更新的细节也不同,通过观察12的平衡因⼦不同,这⾥我们要分三个场景讨论。
•场景1:h>=1时,新增结点插⼊在e⼦树,e⼦树⾼度从h-1变为h并不断更新12->15->10平衡因⼦,引发旋转,其中12的平衡因⼦为-1,旋转后10和12平衡因⼦为0,15平衡因⼦为1。
•场景2:h>=1时,新增结点插⼊在f⼦树,f⼦树⾼度从h-1变为h并不断更新12->15->10平衡因⼦,引发旋转,其中12的平衡因⼦为1,旋转后15和12平衡因⼦为0,10平衡因⼦为-1。
• 场景3:h==0时,a/b/c都是空树,b⾃⼰就是⼀个新增结点,不断更新15->10平衡因⼦,引发旋转,其中12的平衡因⼦为0,旋转后10和12和15平衡因⼦均为0。

2.3.9右左双旋代码实现

2.4.AVL树的查找

2.5.AVL树平衡检测
我们实现的AVL树是否合格,我们通过检查左右⼦树⾼度差的的程序进⾏反向验证,同时检查⼀下结点的平衡因⼦更新是否出现了问题。(空树也是AVL树哦!!!!)


相关文章:

初知C++:AVL树
文章目录 初知C:AVL树1.AVL树的概念2.AVL树的是实现2.1.AVL树的结构2.2.AVL树的插入2.3.旋转2.4.AVL树的查找2.5.AVL树平衡检测 初知C:AVL树 1.AVL树的概念 • AVL树是最先发明的自平衡⼆叉查找树,AVL是⼀颗空树,或者具备下列性…...

[LeetCode] 67. 二进制求和
题目描述: 给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和。 示例 1: 输入:a "11", b "1" 输出:"100" 示例 2: 输入:a "1010", b "…...

工业物联网关-ModbusTCP
Modbus-TCP模式把网关视作Modbus从端设备,主端设备可以通过Modbus-TCP协议访问网关上所有终端设备。用户可以自定义多条通道,每条通道可以配置为TCP Server或者TCP Slave。注意,该模式需要指定采集通道,采集通道可以是串口和网口通…...

子组件向父组件传值$emit
点击子组件的按钮,将子组件的值传递给父组件,并进行提示。 子组件 <template><div><button click"emitIndex">clickme</button></div> </template> <script> export default {methods: {emitInde…...

校车购票微信小程序的设计与实现(lw+演示+源码+运行)
摘 要 由于APP软件在开发以及运营上面所需成本较高,而用户手机需要安装各种APP软件,因此占用用户过多的手机存储空间,导致用户手机运行缓慢,体验度比较差,进而导致用户会卸载非必要的APP,倒逼管理者必须改…...

【Golang】关于Go语言中的定时器原理与实战应用
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...

matlab不小心删除怎么撤回
预设项——>删除文件——>移动至临时文件夹 tem临时文件夹下...

云原生、云计算、虚拟化概念概述
(带着批评阅读,不对的请评论区补充) 1、出现年代前后顺序 虚拟化------>云计算------>云原生 2、虚拟化 虚拟化侧重描述实现,最开始的技术是模拟、hook指令执行软件程序,后续出现了半虚拟化、CPU硬件提供虚拟化…...
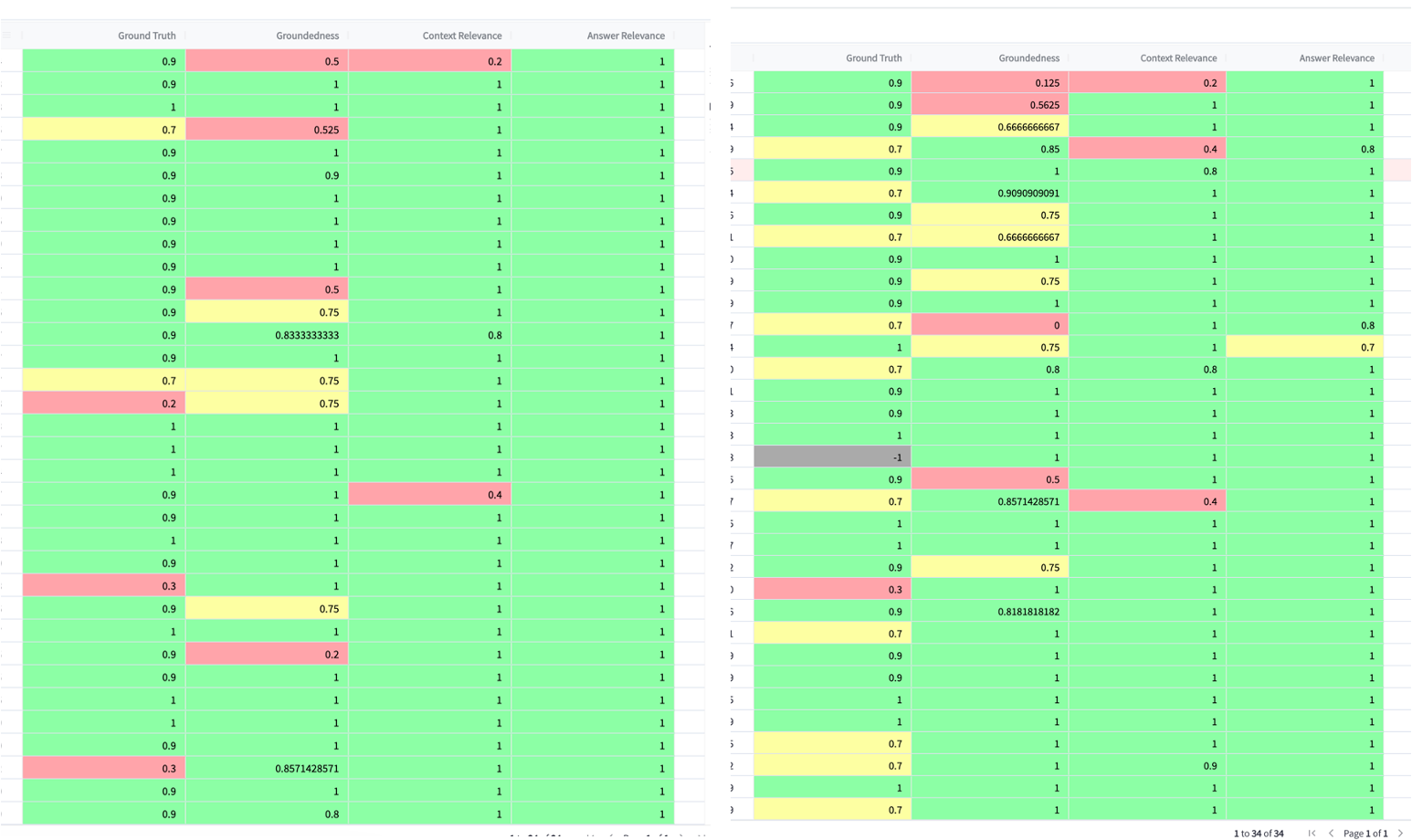
【Trulens框架】用TruLens 自动化 RAG 应用项目评估测试
前言: 什么是Trulens TruLens是面向神经网络应用的质量评估工具,它可以帮助你使用反馈函数来客观地评估你的基于LLM(语言模型)的应用的质量和效果。反馈函数可以帮助你以编程的方式评估输入、输出和中间结果的质量,从而…...

互联网线上融合上门洗衣洗鞋小程序,让洗衣洗鞋像点外卖一样简单
随着服务创新的风潮,众多商家已巧妙融入预约上门洗鞋新风尚,并携手洗鞋小程序,开辟线上蓝海。那么,这不仅仅是一个小程序,它究竟蕴含着哪些诱人好处呢? 1. 无缝融合,双线共赢:小程序…...

R语言绘制三维散点图
之前我们绘制的属于二维散点图,具有两个维度通常是 x 轴和 y 轴)上展示数据点的分布。只能呈现两个变量之间的关系。而三维散点图则具有三个维度(x 轴、y 轴和 z 轴)上展示数据点的分布。可以同时呈现三个变量之间的关系ÿ…...

2014年国赛高教杯数学建模A题嫦娥三号软着陆轨道设计与控制策略解题全过程文档及程序
2014年国赛高教杯数学建模 A题 嫦娥三号软着陆轨道设计与控制策略 嫦娥三号于2013年12月2日1时30分成功发射,12月6日抵达月球轨道。嫦娥三号在着陆准备轨道上的运行质量为2.4t,其安装在下部的主减速发动机能够产生1500N到7500N的可调节推力,…...

QD1-P25 CSS 背景
本节学习:CSS 背景属性 本节视频 https://www.bilibili.com/video/BV1n64y1U7oj?p25 背景颜色 背景图片 不重复 横向重复 纵向重复 双向重复 背景图片大小 400px 600px 原图大小 显示器宽度不够时&…...

《Linux运维总结:基于ARM64+X86_64架构CPU使用docker-compose一键离线部署mongodb 7.0.14容器版分片集群》
总结:整理不易,如果对你有帮助,可否点赞关注一下? 更多详细内容请参考:《Linux运维篇:Linux系统运维指南》 一、部署背景 由于业务系统的特殊性,我们需要面向不通的客户安装我们的业务系统&…...
)
Java利用ChromeDriver插件网页截图(Wondows版+Linux版)
chromedriver是谷歌浏览器驱动,用来模拟谷歌运行操作的一个工具,此处主要讲解Java后端利用此插件进行网页截图,并且适配Linux部署。 环境准备 Wondows服务器或电脑 本机需安装Chrome谷歌浏览器,根据本机浏览器版本,下载对应的chr…...

无人机之交互系统篇
一、系统构成 无人机交互系统通常由多个子系统组成,包括但不限于: 多模式人机交互装置:这是人机交互系统的基础层,通常包括计算机、局域网、传感器等设备,用于实现操作员与无人机之间的数据交互和指令传递。例如&…...

MarsCode--找出数字比例超过n/2的【简单】
问题描述 给定一个长度为n的整型数组,已知其中一个数字的出现次数超过数组长度的一半,找出这个元素 输入格式 一个长度为n的数组,其中某个元素的出现次数大于n/2 输出格式 一个整数 输入样例 [1,3,8,2,3,1,3,3,3] 输出样例 3 数据范…...

Python网络爬虫快速入门指南
Python网络爬虫快速入门指南 网络爬虫,也称为网络蜘蛛,是一种自动访问互联网并提取信息的程序。Python因其简洁明了的语法和丰富的库支持,成为开发网络爬虫的理想选择。在这篇博客中,我们将探讨如何快速入门Python网络爬虫技术&a…...

C86 架构一键离线安装 docker 和 docker-compose 实战指南
C86 架构一键离线安装 docker 和 docker-compose 实战指南 文章目录 C86 架构一键离线安装 docker 和 docker-compose 实战指南一 磁盘挂载二 docker 部署1 上传安装包2 解压安装包3 安装包 docker 三 验证安装四 清除安装包五 安装包下载地址 本文提供了在 C86 架构环境下&…...

【LwIP源码学习2】调试输出相关宏
前言 本文对lwip中debug.h文件里的调试相关宏进行分析。 正文 debug.h中有3个重要的调试相关宏: LWIP_ASSERT(message, assertion) LWIP_ERROR(message, expression, handler) LWIP_DEBUGF(debug, message) 断言 LWIP_ASSERT(message, assertion) 源代码为&…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...
