Java->排序
目录
一、排序
1.概念
2.常见的排序算法
二、常见排序算法的实现
1.插入排序
1.1直接插入排序
1.2希尔排序(缩小增量法)
1.3直接插入排序和希尔排序的耗时比较
2.选择排序
2.1直接选择排序
2.2堆排序
2.3直接选择排序与堆排序的耗时比较
3.交换排序
3.1冒泡排序
3.2快速排序
1. Hoare版
2. 挖坑法
3. 前后指针
3.2.1快速排序的优化
1.三数取中法选key
2. 递归到小的子区间时,可以考虑使用插入排序
3.2.2非递归的快速排序
4.归并排序
1.归并排序
2.非递归的归并排序
3.海量数据的排序问题
5.排序算法复杂度及稳定性分析
编辑
三、其他非基于比较排序
1.计数排序
2.基数排序
3.桶排序
4.比较
5.排序
一、排序
1.概念
所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。

内部排序:数据元素全部放在内存中的排序
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求在内外存之间移动数据的排序
2.常见的排序算法

二、常见排序算法的实现
1.插入排序
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列
1.1直接插入排序
public static void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {int j = i - 1;int tmp = array[i];for (; j >= 0; j--) {if(array[j] > tmp) {
//if(arr[j] >= tmp)
//变为不稳定的排序array[j+1] = array[j];}else {
// array[j+1] = tmp;break;}}array[j+1] = tmp;}}直接插入排序的特性总结:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1),它是一种稳定的排序算法
4. 稳定性:稳定
如果一个排序 本身就是稳定的排序 那么它就可以被实现为不稳定的排序,
但是一个排序 本身就是不稳定的排序 那么它不可能被实现为稳定的排序
1.2希尔排序(缩小增量法)
先选定一个整数,把待排序文件分为整数个组,再进行每个组内的排序

跳跃式分组:

public static void shellSort(int[] array) {int gap = array.length;while(gap > 1) {gap /= 2;shell(array,gap);}}private static void shell(int[] array, int gap) {for (int i = gap; i < array.length; i++) {int j = i - gap;int tmp = array[i];for (; j >= 0; j -= gap) {if(array[j] > tmp) {array[j+gap] = array[j];}else {break;}}array[j+gap] = tmp;}} 希尔排序的特性总结:
1. 希尔排序是对直接插入排序的优化。
2. 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就会很快。这样整体而言,可以达到优化的效果。
3. 希尔排序的时间复杂度不固定:O(N^1.3)....O(N^1.5)
4. 空间复杂度:O(1) ,不稳定
1.3直接插入排序和希尔排序的耗时比较
import java.util.Arrays;
import java.util.Random;public class Text {public static void readyDataOrder(int[] array) {Random random = new Random();for (int i = 0; i < array.length; i++) {array[i] = random.nextInt(100000);}}public static void InsertOrder(int[] array) {array = Arrays.copyOf(array,array.length);long start = System.currentTimeMillis();Sort.insertSort(array);long end = System.currentTimeMillis();System.out.println("插入排序耗时参考:" + (end - start));}public static void ShellOrder(int[] array) {long start = System.currentTimeMillis();Sort.shellSort(array);long end = System.currentTimeMillis();System.out.println("希尔排序耗时参考:" + (end - start));}public static void main(String[] args) {int[] array = new int[100000];readyDataOrder(array);InsertOrder(array);ShellOrder(array);}
}
//插入排序耗时参考:1884
//希尔排序耗时参考:22
2.选择排序
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完
2.1直接选择排序
public static void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIndex = i;for (int j = i + 1; j < array.length; j++) {if (array[j] < array[minIndex]) {minIndex = j;}}swap(array,i,minIndex);}}private static void swap(int[] array, int i, int minIndex) {int tmp = array[i];array[i] = array[minIndex];array[minIndex] = tmp;}直接选择排序的特性总结:
1. 直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}public static void select2Sort(int[] array) {int left = 0;int right = array.length - 1;while(left<right) {int minIndex = left;int maxIndex = left;for (int i = left + 1; i <= right; i++) {if(array[i] < array[minIndex]) {minIndex = i;}if(array[i] > array[maxIndex]) {maxIndex = i;}}swap(array,left,minIndex);//第一个数据是最大值if(maxIndex == left) {maxIndex = minIndex;}swap(array,right,maxIndex);left++;right--;}}
//复杂度不变2.2堆排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆
public static void heapSort(int[] array) {createHeap(array);int end = array.length - 1;while(end > 0) {swap(array,0,end);siftDown(array,0,end);end--;}}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}public static void createHeap(int[] array) {for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) {siftDown(array,parent,array.length);}}private static void siftDown(int[] array,int parent,int len) {int child = parent * 2 + 1;while(child < len) {if(child + 1 < len && array[child] < array[child + 1]) {child++;}if(array[child] > array[parent]) {swap(array,child,parent);parent = child;child = parent * 2 + 1;}else {break;}}}堆排序的特性总结:
1. 堆排序使用堆来选数,效率就高了很多。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(1)
4. 稳定性:不稳定
2.3直接选择排序与堆排序的耗时比较
public class Text {public static void main(String[] args) {int[] array = new int[100000];readyDataOrder(array);InsertOrder(array);ShellOrder(array);selectOrder(array);select2Order(array);heaptOrder(array);}public static void readyDataOrder(int[] array) {Random random = new Random();for (int i = 0; i < array.length; i++) {array[i] = random.nextInt(100000);}}public static void InsertOrder(int[] array) {array = Arrays.copyOf(array,array.length);long start = System.currentTimeMillis();Sort.insertSort(array);long end = System.currentTimeMillis();System.out.println("插入排序耗时参考:" + (end - start));}public static void ShellOrder(int[] array) {array = Arrays.copyOf(array,array.length);long start = System.currentTimeMillis();Sort.shellSort(array);long end = System.currentTimeMillis();System.out.println("希尔排序耗时参考:" + (end - start));}public static void selectOrder(int[] array) {array = Arrays.copyOf(array,array.length);long start = System.currentTimeMillis();Sort.selectSort(array);long end = System.currentTimeMillis();System.out.println("选择排序耗时参考:" + (end - start));}public static void select2Order(int[] array) {array = Arrays.copyOf(array,array.length);long start = System.currentTimeMillis();Sort.select2Sort(array);long end = System.currentTimeMillis();System.out.println("选择排序2耗时参考:" + (end - start));}public static void heaptOrder(int[] array) {array = Arrays.copyOf(array,array.length);long start = System.currentTimeMillis();Sort.heapSort(array);long end = System.currentTimeMillis();System.out.println("堆排序耗时参考:" + (end - start));}
}
//插入排序耗时参考:2098
//希尔排序耗时参考:25
//选择排序耗时参考:4093
//选择排序2耗时参考:2929
//堆排序耗时参考:163.交换排序
所谓交换,就是根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置,交换排序的特点是:将键值较大的记录向序列的尾部移动,键值较小的记录向序列的前部移动。
3.1冒泡排序
public static void bubbleSort(int[] array) {//i是趟数for (int i = 0; i < array.length - 1; i++) {for (int j = 0; j < array.length - 1 - i; j++) {if(array[j] > array[j+1]) {swap(array,j,j+1);}}}}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}冒泡排序的特性总结:
1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度:O(N^2)
3. 空间复杂度:O(1)
4. 稳定性:稳定
优化:
public static void bubbleSort(int[] array) {//i是趟数for (int i = 0; i < array.length - 1; i++) {boolean flg = true;for (int j = 0; j < array.length - 1 - i; j++) {if(array[j] > array[j+1]) {swap(array,j,j+1);flg = false;}}if(flg) {break;}}}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}3.2快速排序
任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止
1. Hoare版
public static void quickSort(int[] array) {quick(array,0,array.length - 1);}private static void quick(int[] array, int left, int right) {if(left > right) return;int par = partition(array,left,right);quick(array,left,par-1);quick(array,par+1,right);}private static int partition(int[] array, int start, int end) {int i = start;int pivot = array[start];while(start < end) {
//先end后startwhile(start < end && array[end] >= pivot) {end--;}while(start < end && array[start] <= pivot) {start++;}swap(array,start,end);}swap(array,i,start);return start;}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}快速排序的特性总结:
1. 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
2. 时间复杂度:O(N*logN) 如果的是1 2 3 4 5 或 5 4 3 2 1…… 单分支的树时间复杂度为O(N^2),但一般不说快排时间复杂度为O(N^2),
3. 空间复杂度:O(logN) 单分支的树空间复杂度为O(N)
4. 稳定性:不稳定
//插入排序耗时参考:1983
//希尔排序耗时参考:19
//选择排序耗时参考:3844
//选择排序2耗时参考:2977
//堆排序耗时参考:14
//冒泡排序耗时参考:20525
//快速排序耗时参考:112. 挖坑法
public static void quickSort(int[] array) {quick(array,0,array.length - 1);}private static void quick(int[] array, int left, int right) {if(left > right) return;int par = partition(array,left,right);quick(array,left,par-1);quick(array,par+1,right);} private static int partition(int[] array,int start,int end) {int pivot = array[start];while(start < end) {while(start < end && array[end] >= pivot) {end--;}array[start] = array[end];while(start < end && array[start] <= pivot) {start++;}array[end] = array[start];}array[start] = pivot;return start;}3. 前后指针
public static void quickSort(int[] array) {quick(array,0,array.length - 1);}private static void quick(int[] array, int left, int right) {if(left > right) return;int par = partition(array,left,right);quick(array,left,par-1);quick(array,par+1,right);}private static int partition(int[] array,int start,int end) {int prev = start;int cur = start + 1;while(cur <= end) {if(array[cur] < array[start] && array[++prev] != array[cur]) {swap(array,cur,prev);}cur++;}swap(array,prev,start);return prev;}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}3.2.1快速排序的优化
1.三数取中法选key
private static void quick(int[] array, int left, int right) {if(left > right) return;int index = midThreeNum(array,left,right);swap(array,index,left);int par = partition(array,left,right);quick(array,left,par-1);quick(array,par+1,right);}//三数取中法选keypublic static int midThreeNum(int[] array, int start, int end) {int mid = (start + end) / 2;if(array[start] < array[end]) {if(array[mid] < array[start]){return start;}else if(array[mid] > array[end]) {return end;}else {return mid;}}else {if(array[mid] > array[start]){return start;}else if(array[mid] < array[end]) {return end;}else {return mid;}}}2. 递归到小的子区间时,可以考虑使用插入排序
public static void quickSort(int[] array) {quick(array,0,array.length - 1);}private static void quick(int[] array, int left, int right) {if(left > right) return;if(right - left + 1 == 7) {insertSort2(array,left,right);}int index = midThreeNum(array,left,right);swap(array,index,left);int par = partition(array,left,right);quick(array,left,par-1);quick(array,par+1,right);}//三数取中法选keypublic static int midThreeNum(int[] array, int start, int end) {int mid = (start + end) / 2;if(array[start] < array[end]) {if(array[mid] < array[start]){return start;}else if(array[mid] > array[end]) {return end;}else {return mid;}}else {if(array[mid] > array[start]){return start;}else if(array[mid] < array[end]) {return end;}else {return mid;}}}//递归到小的子区间时,可以考虑使用插入排序private static void insertSort2(int[] array ,int start,int end) {for (int i = start + 1; i <= end; i++) {int j = i - 1;int tmp = array[i];for (; j >= start; j--) {if (array[j] > tmp) {array[j + 1] = array[j];} else {
// array[j+1] = tmp;break;}}array[j + 1] = tmp;}}private static int partition(int[] array, int start, int end) {int i = start;int pivot = array[start];while(start < end) {while(start < end && array[end] >= pivot) {end--;}while(start < end && array[start] <= pivot) {start++;}swap(array,start,end);}swap(array,i,start);return start;}3.2.2非递归的快速排序
public static void quickSort2(int[] array) {int left = 0;int right = array.length - 1;int par = partition(array,left,right);Stack<Integer> stack = new Stack<>();if(par > left + 1) {stack.push(left);stack.push(par - 1);}if(par < right - 1) {stack.push(par + 1);stack.push(right);}while(!stack.isEmpty()) {right = stack.pop();left = stack.pop();par = partition(array,left,right);if(par > left + 1) {stack.push(left);stack.push(par - 1);}if(par < right - 1) {stack.push(par + 1);stack.push(right);}}}private static int partition(int[] array, int start, int end) {int i = start;int pivot = array[start];while(start < end) {while(start < end && array[end] >= pivot) {end--;}while(start < end && array[start] <= pivot) {start++;}swap(array,start,end);}swap(array,i,start);return start;}4.归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并
1.归并排序

public static void mergeSort(int[] array) {mergeSortFunc(array,0,array.length - 1);}private static void mergeSortFunc(int[] array,int left,int right) {if(left == right) return;int mid =(left + right) / 2;//分解mergeSortFunc(array,left,mid);mergeSortFunc(array,mid+1,right);//合并merge(array,left,right,mid);}private static void merge(int[] array, int left, int right, int mid) {int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;int[] tmpArr = new int[right - left + 1];int k = 0;while(s1<=e1 && s2<=e2) {if(array[s1] < array[s2]) {tmpArr[k++] = array[s1++];}else {tmpArr[k++] = array[s2++];}}while(s1<=e1) {tmpArr[k++] = array[s1++];}while(s2<=e2) {tmpArr[k++] = array[s2++];}for (int i = 0; i < tmpArr.length; i++) {array[i+left] = tmpArr[i];}}归并排序的特性总结:
1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(N)
4. 稳定性:稳定
//插入排序耗时参考:2301
//希尔排序耗时参考:25
//选择排序耗时参考:4710
//选择排序2耗时参考:3635
//堆排序耗时参考:25
//冒泡排序耗时参考:23906
//快速排序耗时参考:40
//归并排序耗时参考:422.非递归的归并排序
public static void mergeSort(int[] array) {int gap = 1;while (gap < array.length) {for (int i = 0; i < array.length; i += 2*gap) {int left = i;int mid = left + gap - 1;int right = mid + gap;if (mid >= array.length) {mid = array.length - 1;}if (right >= array.length) {right = array.length - 1;}merge(array, left, right, mid);}gap *= 2;}}private static void merge(int[] array, int left, int right, int mid) {int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;int[] tmpArr = new int[right - left + 1];int k = 0;while (s1 <= e1 && s2 <= e2) {if (array[s1] < array[s2]) {tmpArr[k++] = array[s1++];} else {tmpArr[k++] = array[s2++];}}while (s1 <= e1) {tmpArr[k++] = array[s1++];}while (s2 <= e2) {tmpArr[k++] = array[s2++];}for (int i = 0; i < tmpArr.length; i++) {array[i + left] = tmpArr[i];}}3.海量数据的排序问题
外部排序:排序过程需要在磁盘等外部存储进行的排序
前提:内存只有 1G,需要排序的数据有 100G
因为内存中因为无法把所有数据全部放下,所以需要外部排序,而归并排序是最常用的外部排序
1. 先把文件切分成 200 份,每个 512 M
2. 分别对 512 M 排序,因为内存已经可以放的下,所以任意排序方式都可以
3. 进行 2路归并,同时对 200 份有序文件做归并过程,最终结果就有序了
5.排序算法复杂度及稳定性分析
| 排序方法 | 最好 | 平均 | 最坏 | 空间复杂度 | 稳定性 |
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 希尔排序 | O(n) | O(n^1.3) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(1) | 不稳定 |
| 快速排序 | O(n * log(n)) | O(n * log(n)) | O(n^2) | O(log(n)) ~ O(n) | 不稳定 |
| 归并排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(n) | 稳定 |
三、其他非基于比较排序
1.计数排序
计数排序的场景一定是数据集中在某各范围中
步骤:
1. 统计相同元素出现次数
2. 根据统计的结果将序列回收到原来的序列中
public static void countSort(int[] array) {//1.求 最大值 最小值 来确定 计数数组的大小int min = array[0];int max = array[0];for (int i = 1; i < array.length; i++) {if(array[i] < min) {min = array[i];}if(array[i] > max) {max = array[i];}}int len = max - min + 1;int[] count = new int[len];//2.遍历原来的数组 存放元素到计数数组中
//O(N)for (int i = 0; i < array.length; i++) {int index = array[i] - min;count[index]++;}//3.遍历计数数组
//O(范围)int arrIndex = 0;for (int i = 0; i < count.length; i++) {while(count[i]!=0) {array[arrIndex] = i + min;arrIndex++;count[i]--;}}时间复杂度:O(范围 + N )
空间复杂度:O(范围)
稳定性:稳定
2.基数排序
动态图
队列,桶
3.桶排序
划分多个范围相同的区间,每个子区间自排序,最后合并

public static void bucketSort(int[] array){// 计算最大值与最小值int max = array[0];int min = array[0];for(int i = 1; i < array.length; i++){if(array[i] < min) {min = array[i];}if(array[i] > max) {max = array[i];}}// 计算桶的数量int bucketNum = (max - min) / array.length + 1;ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);for(int i = 0; i < bucketNum; i++){bucketArr.add(new ArrayList<Integer>());}// 将每个元素放入桶for(int i = 0; i < array.length; i++){int num = (array[i] - min) / (array.length);bucketArr.get(num).add(array[i]);}// 对每个桶进行排序for(int i = 0; i < bucketArr.size(); i++){Collections.sort(bucketArr.get(i));}// 将桶中的元素赋值到原序列int index = 0;for(int i = 0; i < bucketArr.size(); i++){for(int j = 0; j < bucketArr.get(i).size(); j++){array[index++] = bucketArr.get(i).get(j);}}}4.比较
- 基数排序:根据键值的每位数字来分配桶;
- 计数排序:每个桶只存储单一键值;
- 桶排序:每个桶存储一定范围的数值;
5.排序
相关文章:

Java->排序
目录 一、排序 1.概念 2.常见的排序算法 二、常见排序算法的实现 1.插入排序 1.1直接插入排序 1.2希尔排序(缩小增量法) 1.3直接插入排序和希尔排序的耗时比较 2.选择排序 2.1直接选择排序 2.2堆排序 2.3直接选择排序与堆排序的耗时比较 3.交换排序 3.1冒泡排序…...

linux 大小写转换
var"TM_card_INFo" # 把变量中的第一个字符换成大写 echo ${var^} # 把变量中的所有小写字母,全部替换为大写 echo ${var^^} # 把变量中的第一个字符换成小写 echo ${var,} # 把变量中的所有大写字母,全部替换为小写 echo ${var,,} 参考…...

Linux——传输层协议
目录 一再谈端口号 1端口号范围划分 2两个问题 3理解进程与端口号的关系 二UDP协议 1格式 2特点 3进一步理解 3.1关于UDP报头 3.2关于报文 4基于UDP的应用层协议 三TCP协议 1格式 2TCP基本通信 2.1关于可靠性 2.2TCP通信模式 3超时重传 4连接管理 4.1建立…...

centos系列,yum部署jenkins2.479.1,2024年长期支持版本
centos系列,yum部署jenkins2.479.1,2024年长期支持版本 0、介绍 注意:jenkins建议安装LTS长期支持版本,而不是安装每周更新版本,jenkins安装指定版本 openjdk官网下载 Index of /jenkins/redhat-stable/ | 清华大学开…...

正则表达式-“三剑客”(grep、sed、awk)
1.3正则表达式 正则表达式描述了一种字符串匹配的模式,可以用来检查一个串是否含有某种子串,将匹配的子串替换或者从某个串中取出符号某个条件的子串等,在linux中代表自定义的模式模版,linux工具可以用正则表达式过滤文本。Linux…...

数智时代的新航向:The Open Group 2024生态系统架构·可持续发展年度大会邀您共筑AI数字新时代
在全球可持续发展和数字化转型双重驱动下,企业正面临着前所未有的挑战与机遇。如何在激烈的市场竞争中,实现业务增长的同时,履行社会责任,达成可持续发展的目标?The Open Group 2024生态系统架构可持续发展年度大会将于…...

TensorFlow 的核心概念
TensorFlow 是一个开源的机器学习框架,由 Google 开发和维护。它提供了一个强大的工具集,用于构建和训练各种机器学习模型。 TensorFlow 的核心概念是计算图(Computational Graph)。计算图由节点(Nodes)和…...

SpringBoot教程(二十四) | SpringBoot实现分布式定时任务之Quartz(动态新增、修改等操作)
SpringBoot教程(二十四) | SpringBoot实现分布式定时任务之Quartz(动态新增、修改等操作) 前言数据库脚本创建需要被调度的方法创建相关实体类创建业务层接口创建业务层实现类控制层类测试结果 前言 我这边的SpringBoot的版本为2…...

Matlab详细学习教程 MATLAB使用教程与知识点总结
Matlab语言教程 章节目录 一、Matlab简介与基础操作 二、变量与数据类型 三、矩阵与数组操作 四、基本数学运算与函数 五、图形绘制与数据可视化 六、控制流与逻辑运算 七、脚本与函数编写 八、数据导入与导出 九、Matlab应用实例分析 一、Matlab简介与基础操作 重点内容知识…...

【ELKB】Kibana使用
搭建好ELKB后访问地址:http://localhost:5601 输入账号密码登录以后 左侧导航有home、Analysis、Enterprise search 、Observability、Security、Management home:首页Analysis:工具来分析及可视化数据Enterprise search:企业级搜…...

ChatGPT免费使用:人工智能在现代社会中的作用
随着人工智能技术的不断发展,越来越多的应用程序和工具开始使用GPT作为其语言模型。但是,这些应用程序和工具是否收费?如果是免费的,那么他们是如何盈利的?在本文中,我们将探讨ChatGPT免费使用的背后原理&a…...
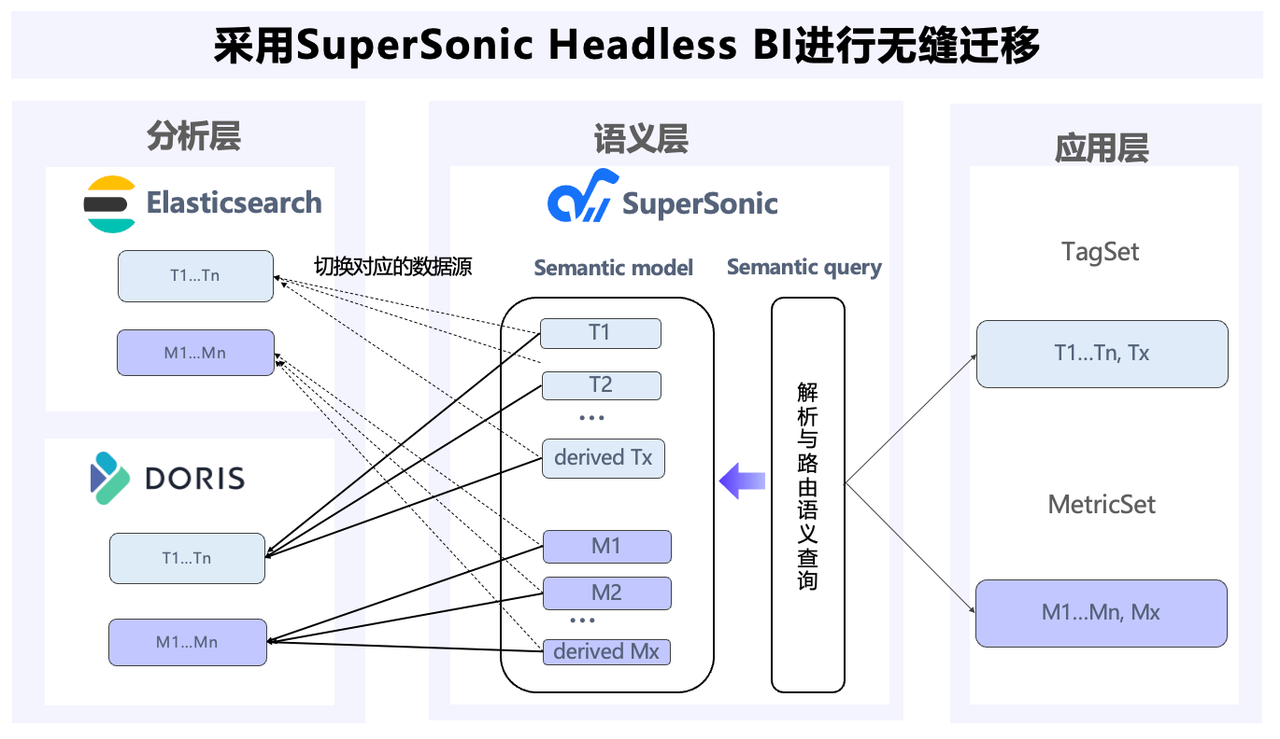
腾讯音乐:从 Elasticsearch 到 Apache Doris 内容库升级,统一搜索分析引擎,成本直降 80%
导读: 为满足更严苛数据分析的需求,腾讯音乐借助 Apache Doris 替代了 Elasticsearch 集群,统一了内容库数据平台的内容搜索和分析引擎。并基于 Doris 倒排索引和全文检索的能力,支持了复杂的自定义标签计算,实现秒级查…...

CubeMX的FreeRTOS学习
一、FreeRTOS的介绍 什么是FreeRTOS? Free即免费的,RTOS的全称是Real Time Operating system,中文就是实时操作系统。 注意:RTOS不是指某一个确定的系统,而是指一类的操作系统。比如:us/OS,FreeRTOS&…...

C语言初始:数据类型和变量
、 一.数据类型介绍 人有黄人白人黑人,那么数据呢? 我们大家可以看出谁是黄种人,谁是白种人,谁是黑种人,这是因为他们是类似的。 数据也是有类型的,就譬如整数类型,字符类型,浮点…...

Linux shellcheck工具
安装工具 通过linux yum源下载,可能因为yum源的问题找不到软件包,或者下载的软件包版本太旧。 ShellCheck的源代码托管在GitHub上(推荐下载方式): GitHub - koalaman/shellcheck: ShellCheck, a static analysis tool for shell scripts 对下…...

FLINK SQL时间属性
Flink三种时间属性简介 在Flink SQL中,时间属性是一个核心概念,它主要用于处理与时间相关的数据流。Flink支持三种时间属性:事件时间(event time)、处理时间(processing time)和摄入时间&#…...

android——Groovy gralde 脚本迁移到DSL
1、implementation的转换 implementation com.github.CymChad:BaseRecyclerViewAdapterHelper:*** 转换为 implementation ("com.github.CymChad:BaseRecyclerViewAdapterHelper:***") 2、plugin的转换 apply plugin: kotlin-android-extensions 转换为&#x…...

工程项目管理中的最常见概念!蓝燕云总结!
01 怎么理解工程项目管理? 建设工程项目管理指的是专业性的管理,并非行政事务管理。建设工程项目管理是对工程项目全生命周期的管理,确保项目能够按计划的进度、成本和质量完成。 建设工程项目不同阶段管理的主要内容不同,通常…...

PostgreSQL AUTO INCREMENT
PostgreSQL AUTO INCREMENT 在数据库管理系统中,自动递增(AUTO INCREMENT)是一种常见特性,用于在插入新记录时自动生成唯一的标识符。PostgreSQL,作为一个功能强大的开源关系数据库管理系统,也提供了类似的…...

24-10-13-读书笔记(二十五)-《一只特立独行的猪》([中] 王小波)用一生来学习艺术
文章目录 《一只特立独行的猪》([中] 王小波)目录阅读笔记记录总结 《一只特立独行的猪》([中] 王小波) 十月第五篇,放慢脚步,秋季快要过去了,要步入冬季了,心中也是有些跌宕起伏&am…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

