2012年国赛高教杯数学建模D题机器人避障问题解题全过程文档及程序
2012年国赛高教杯数学建模
D题 机器人避障问题
图1是一个800×800的平面场景图,在原点O(0, 0)点处有一个机器人,它只能在该平面场景范围内活动。图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物,障碍物的数学描述如下表:

在图1的平面场景中,障碍物外指定一点为机器人要到达的目标点(要求目标点与障碍物的距离至少超过10个单位)。规定机器人的行走路径由直线段和圆弧组成,其中圆弧是机器人转弯路径。机器人不能折线转弯,转弯路径由与直线路径相切的一段圆弧组成,也可以由两个或多个相切的圆弧路径组成,但每个圆弧的半径最小为10个单位。为了不与障碍物发生碰撞,同时要求机器人行走线路与障碍物间的最近距离为10个单位,否则将发生碰撞,若碰撞发生,则机器人无法完成行走。
机器人直线行走的最大速度为v=v(ρ)=v_0/(1+e(10-0.1ρ2 ) )个单位/秒。机器人转弯时,最大转弯速度为 ,其中 是转弯半径。如果超过该速度,机器人将发生侧
翻,无法完成行走。
请建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型。对场景图中4个点O(0, 0),A(300, 300),B(100, 700),C(700, 640),具体计算:
(1) 机器人从O(0, 0)出发,O→A、O→B、O→C和O→A→B→C→O的最短路径。
(2) 机器人从O (0, 0)出发,到达A的最短时间路径。
注:要给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标以及机器人行走的总距离和总时间。

整体求解过程概述(摘要)
针对机器人避障问题,本文分别建立了机器人从区域中一点到达另一点的避障的最短路径、最短时间路径的非线性0-1整数规划模型。同时,本文为求带有NP属性的非线性0-1整数规划模型,构建了有效启发式算法,利用MATLAB软件编程,求得了O→A、O→B、O→C、O→A→B→A→C的最短路径,同时得到了O→A的最短时间路径,求得的各类最短路径均是全局最优。
针对区域中一点到达另一点的避障的最短路径问题,首先,本文证明了圆弧位置设定在需要绕过障碍物的顶角上,且圆弧半径为10个单位时,能够使得机器人从区域中一点到达另一点的行进路径最短;其次,本文将最短路径选择问题转化成了最短路径的优选问题,根据避障条件,建立了具有较高普适性的避障最短路径的优化模型。为便于求解,本文巧妙地将此优化模型转化成了以可行路径不与障碍物边界相交、不与圆弧相交为约束条件,以机器人从区域中一点达到另一点避障路径最短为目标的0-1规划模型;再次,本文构建了两种有效的启发式算法,利用MATLAB软件编程求得了O→A、O→B、O→C、O→A→B→A→C的最短路径,最短路径长分别为471.0372、853.7001、1088.1952、2725.1596,其中O–>A的最短路径为(0,0)→(70.5063,213.1405) →(75.975,219.1542)→(300,300),对应圆弧的圆心坐标为(80,210),O→B的最短路径,对应圆弧的圆心坐标:(60,300)、(150,435)、(220、470)、(220,530)、(150,600), O→C经过的圆心:(410,100)、(230,60)、(720,520),(720,600),(500,200), O→A→B→C→O经过的圆心:(410,100),(230,60), (80,210),(220,530),(150,600),(270,680),(370,680), (430,680),(670,730),(540,730),(720,520),(720,600),(500,200)。
针对最短时间路径问题,我们建立了从o点出发到任意目标点的0-1非线性整数规划模型,同时针对题意要求,具体构建了从o点出发到A的最短时间路径的0-1非线性整数规划模型,利用LINGO软件求解,获得了机器人从o点出发,到达A的最短时间路径,求得最短时间路径下转弯半径为12.9885 ,同时最短时间路径时间长为94.2283个单位。相应圆弧的圆心坐标为(82.1414,207.9153),两切点坐标分别为(69.8045,211.9779)、(77.7492,220.1387)。
模型假设:
1.将机器人看成一个质点;
2.半径不变时,机器人在行进、转弯过程中能一直保持最大的速度;
3.机器人行走过程中不会意外停止;
4.忽略影响机器人行走非最小转弯半径以及最小安全距离因素。
问题分析:
求取最短路径的分析
本问题要求机器人从区域中一点到达另一点的避障最短路径。机器人只要做到转弯时的圆弧半径最小为10个单位、与障碍物最近距离单时刻保持大于10个单位,那么可行走的路径就有无数条,若想求得机器人从区域中一点到达另一点的避障最短路径,则需要建立避障的最短路径模型,而建立避障的最短路径模型有一定难度。根据对问题的分析,我们认为可以从简单做起,先确定小范围内最短路径条件,如圆弧位置的影响,圆弧半径的大小,避免与障碍物碰撞条件等,通过确定最短路径条件来建立避障的最短路径模型。对于最短路径的求取,我们可以通过确定穷举原则,利用穷举法来求解,当然也可以通过构建启发式算法的进行求解。
最短时间路径的分析
对于要建立最短时间路径模型来说,我们容易知道影响的因素有直线行走速度、转弯速度,同时还需要考虑使得最短时间路径条件,如圆弧位置(坐标)的影响,圆弧半径的大小,避免与障碍物碰撞条件等。对于直线行进,我们希望行进速度越大越好,对于机器人转弯时,转弯速度要有约束,要保证机器人不能发生侧翻。我们发现圆弧半径的大小与转弯速度紧密相连,从转弯速度公式来分析,当转弯半径增大时,最大转弯速度也增大,为在更短时间内行进到目标点,我们希望转弯速度为机器人的最大转弯速度较好,但有很大的可能是行进的路径不是最短的,即行进路径有很大可能在增加。于是,我们需要做的工作是,在满足最短时间路径条件时,找到一个圆弧的坐标位置,同时确定半径的大小,以求得最短时间路径。
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
function mind=distancebetweenlines(A,B,C,D,M)
Ax=A(1);Ay=A(2);
Bx=B(1);By=B(2);
Cx=C(1);Cy=C(2);
Dx=D(1);Dy=D(2);
if (A(1)-B(1))~=0k=(By-Ay)/(Bx-Ax);b=By-k*Bx;ABXXL=linspace(A(1),B(1),M);ABYXL=k.*ABXXL+b;
elseABXXL=linspace(A(1),B(1),M);ABYXL=linspace(A(2),B(2),M);
end
if (C(1)-D(1))~=0k=(Dy-Cy)/(Dx-Cx);b=Dy-k*Dx;CDXXL=linspace(C(1),D(1),M);CDYXL=k.*CDXXL+b;
elseCDXXL=linspace(C(1),D(1),M);CDYXL=linspace(C(2),D(2),M);
end
mind=100000;
for i=1:Mfor j=1:Mif sqrt((ABXXL(i)-CDXXL(j))^2+(ABYXL(i)-CDYXL(j))^2)<=mindmind=sqrt((ABXXL(i)-CDXXL(j))^2+(ABYXL(i)-CDYXL(j))^2);endend
end
clear
clc
close all
theta=0:pi/100:2*pi;
zb{1}=[300 400;500 400;500 600;300 600];
zb{2}=[550 450;70 70];
zb{3}=[360 240;400 330;540 330;500 240];
zb{4}=[280 100;345 210;410 100];
zb{5}=[80 60;80 150+60;150+80 150+60;150+80 60;];
zb{6}=[60 300; 150 435;235 300];
zb{7}=[0 470;220 470;220 530;0 530];
zb{8}=[150 600;240 600;270 680;180 680];
zb{9}=[370 680;430 680;430 800;370 800];
zb{10}=[540 600;670 600;670 730;540 730];
zb{11}=[640 520;720 520;720 600;640 600];
zb{12}=[500 140;800 140;800 200;500 200];
zb{13}=[0 0;0 800;800 800;800 0;];
zb{14}=[0 0 79];
zb{15}=[300 300 65];
zb{16}=[100 700 66];
zb{17}=[700 640 67];
for i=1:length(zb)temp=zb{i};if size(zb{i},1)==2x=temp(2,1)*cos(theta)+temp(1,1);y=temp(2,2)*sin(theta)+temp(1,2);plot(x,y,'r-');hold onelseif size(zb{i},1)==3for j=1:length(temp)plot([temp(:,1);temp(1,1)],[temp(:,2);temp(1,2)],'b-');hold onendelseif size(zb{i},1)==4for j=1:length(temp)plot([temp(:,1);temp(1,1)],[temp(:,2);temp(1,2)],'b-');hold onendelseif size(zb{i},1)==1plot(temp(1),temp(2),'r.','MarkerSize',12);text(temp(1)+10,temp(2)+20,char(temp(3)));hold onendif i<=12&i~=2for j=1:size(temp,1)temp1=temp(j,:);x=10*cos(theta)+temp1(1);y=10*sin(theta)+temp1(2);plot(x,y,'r-');hold onendend
end
axis([0 800 0 800]);grid on
hold off
%下面计算切点坐标
for i=1:4x=[];y=[];kk=1;temp=zb{13+i};A=temp(1:2);for j=1:12temp2=zb{j};if j==2r=70;temp2=temp2(1,:);elser=10;endfor k=1:size(temp2,1)B=temp2(k,:);if ~ismember(B(1),[0,800]) & ~ismember(B(2),[0,800])[x(:,kk) y(:,kk)]=qiedian(A,B,r);kk=kk+1;endendendqdzb(:,:,i)=[reshape(x,1,2*length(x));reshape(y,1,2*length(y))];
end
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2012年国赛高教杯数学建模D题机器人避障问题解题全过程文档及程序
2012年国赛高教杯数学建模 D题 机器人避障问题 图1是一个800800的平面场景图,在原点O(0, 0)点处有一个机器人,它只能在该平面场景范围内活动。图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物,障碍物的数学描述如下表:…...

Linux驱动开发——设备树
文章目录 1 什么是设备树?2 DTS、DTB和DTC3 DTS语法3.1 dtsi头文件3.2 设备节点3.3 标准属性3.4 根节点compatible属性3.5 向节点追加或修改内容 4 创建小型模板设备树5 设备树在系统中的体现6 绑定信息文档7 设备树常用OF操作函数7.1 查找节点的OF函数7.2 查找父/子…...

spring boot 2.7整合Elasticsearch Java client + ingest attachment实现文档解析
一、软件环境 软件版本号备注Spring boot2.7.23.x版本建议使用ElasticSearch8.xElasticSearch7.17.4ElasticSearch 7.x 可使用JDK 8 ElasticSearch 8.x 要求使用JDK 11 二、安装ElasticSearch 下载地址:https://artifacts.elastic.co/downloads/elasticsearch/el…...

一、PyCharm 基本快捷键总结
PyCharm 快捷键 前言一、编辑(Editing)二、查找/替换(Replace)三、运行(Running)四、重构(Refactoring)五、基本(General) 前言 下面我们将学习一些 Pycharm 中的快捷键来帮我们更好的使用工具。 一、编辑(Editing) 快捷键快捷键…...
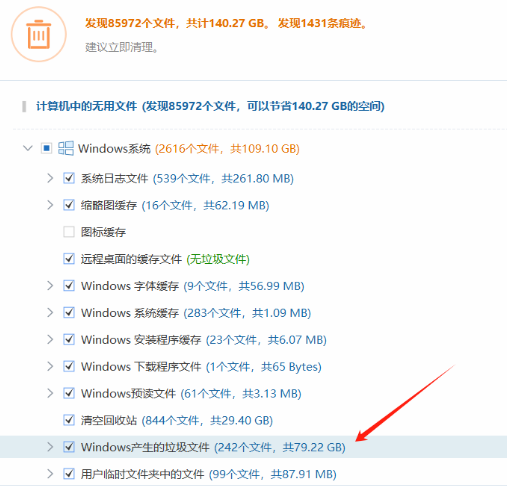
Windows系统C盘爆满了,如何清理?
Windows系统C盘爆满了,如何清理? 大家好,我是秋意零。 相信使用过Windows系统的朋友,都见过C盘那道靓丽的 “红色风景线” ! 我自己的Win10系统,已经使用了4-5年时间了。最近频频出现"红色风景线&q…...

【C++】踏上C++学习之旅(一):初识C++和命名空间
文章目录 前言1. 初识C2. C的发展阶段2. 命名空间2.1 为什么要有命名空间?2.2 命名空间的语法2.3 命名空间的原理2.4 使用命名空间的三种方式2.4.1 加命名空间名称及作用域限定符( :: )2.4.2 使用using关键字将命名空间中某个成员 引入2.4.3 使用using namespace 命…...

tensorflow入门案例手写数字识别人工智能界的helloworld项目落地1
参考 https://tensorflow.google.cn/?hlzh-cn https://tensorflow.google.cn/tutorials/keras/classification?hlzh-cn 项目资源 https://download.csdn.net/download/AnalogElectronic/89872174 文章目录 一、案例学习1、导入测试和训练数据集,定义模型ÿ…...

深度学习——线性神经网络(三、线性回归的简洁实现)
目录 3.1 生成数据集3.2 读取数据集3.3 定义模型3.4 初始化模型参数3.5 定义损失函数3.6 定义优化算法3.7 训练 在上一节中,我们通过张量来自定义式地进行数据存储和线性代数运算,并通过自动微分来计算梯度。实际上,由于数据迭代器、损失函数…...

本地部署 Milvus
本地部署 Milvus 1. Install Milvus in Docker2. Install Attu, an open-source GUI tool 1. Install Milvus in Docker curl -sfL https://raw.githubusercontent.com/milvus-io/milvus/master/scripts/standalone_embed.sh -o standalone_embed.shbash standalone_embed.sh …...

Git基础-配置http链接的免密登录
问题描述 当我们在使用 git pull 或者 git push 进行代码拉取或代码提交时, 若我们的远程代码仓库是 http协议的链接时,就是就会提示我们进行账号密码的登录。 每次都要登录,这未免有些麻烦。 本文介绍一下免密登录的配置。解决方案 1 执行…...
)
华为OD机试真题-编码能力提升-2024年OD统一考试(E卷)
最新华为OD机试考点合集:华为OD机试2024年真题题库(E卷+D卷+C卷)_华为od机试题库-CSDN博客 每一题都含有详细的解题思路和代码注释,精编c++、JAVA、Python三种语言解法。帮助每一位考生轻松、高效刷题。订阅后永久可看,持续跟新。 题目描述 为了提升软件编码能力,小…...
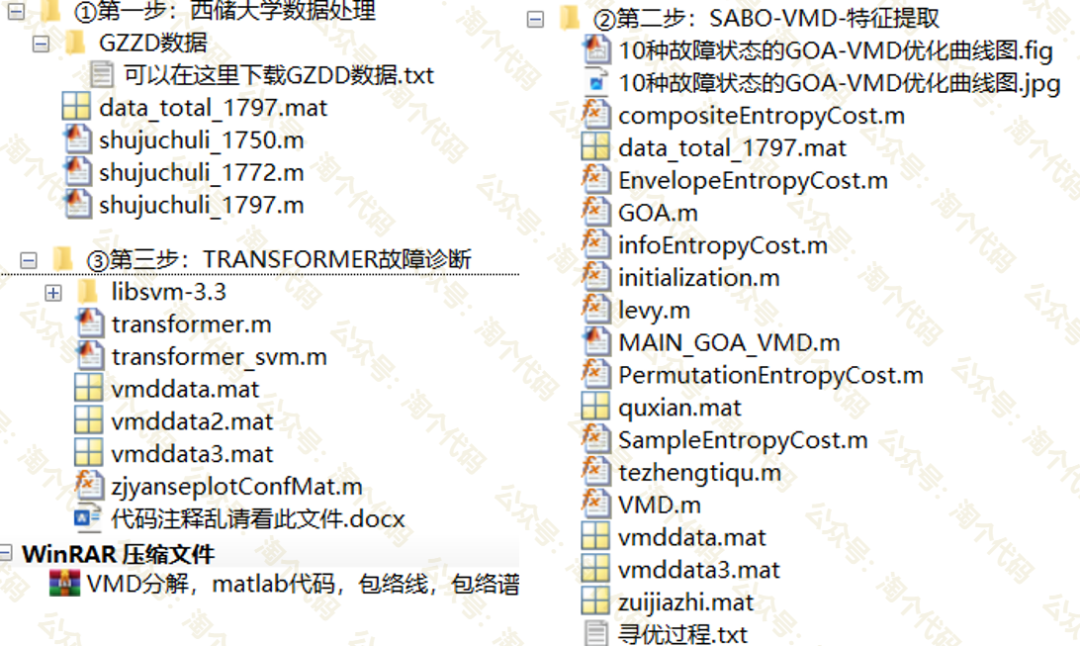
高被引算法GOA优化VMD,结合Transformer-SVM的轴承诊断,保姆级教程!
本期采用2023年瞪羚优化算法优化VMD,并结合Transformer-SVM实现轴承诊断,算是一个小创新方法了。需要水论文的童鞋尽快! 瞪羚优化算法之前推荐过,该成果于2023年发表在计算机领域三区SCI期刊“Neural Computing and Applications”…...

半小时速通RHCSA
1-7章: #01创建以上目录和文件结构,并将/yasuo目录拷贝4份到/目录下 #02查看系统合法shell #03查看系统发行版版本 #04查看系统内核版本 #05临时修改主机名 #06查看系统指令的查找路径 #07查看passwd指令的执行路径 #08为/yasuo/ssh_config文件在/mulu目录下创建软链…...

人工智能和机器学习之线性代数(一)
人工智能和机器学习之线性代数(一) 人工智能和机器学习之线性代数一将介绍向量和矩阵的基础知识以及开源的机器学习框架PyTorch。 文章目录 人工智能和机器学习之线性代数(一)基本定义标量(Scalar)向量&a…...

STM32外设应用详解
STM32外设应用详解 STM32微控制器是意法半导体(STMicroelectronics)推出的一系列基于ARM Cortex-M内核的高性能、低功耗32位微控制器。它们拥有丰富的外设接口和功能模块,可以满足各种嵌入式应用需求。本文将详细介绍STM32的外设及其应用&am…...
优化配置)
docker详解介绍+基础操作 (三)优化配置
1.docker 存储引擎 Overlay: 一种Union FS文件系统,Linux 内核3.18后支持 Overlay2:Overlay的升级版,docker的默认存储引擎,需要磁盘分区支持d-type功能,因此需要系统磁盘的额外支持。 关于 d-type 传送…...

细说Qt的状态机框架及其用法
文章目录 使用场景基本用法状态定义添加转换历史状态QStateMachine是Qt框架中用于构建状态机的一个类,它属于Qt的状态机框架(State Machine Framework)。这个框架提供了一种模型,用于设计响应不同事件(如用户输入、文件I/O或网络活动)的应用程序的行为。通过使用状态机,开发…...

Oracle-表空间与数据文件操作
目录 1、表空间创建 2、表空间修改 3、数据文件可用性切换操作 4、数据文件和表空间删除 1、表空间创建 (1)为 ORCL 数据库创建一个名为 BOOKTBS1 的永久表空间,数据文件为d:\bt01.dbf ,大小为100M,区采用自动扩展…...

C# WinForm实现画笔签名及解决MemoryBmp格式问题
目录 需求 实现效果 开发运行环境 设计实现 界面布局 初始化 画笔绘图 清空画布 导出位图数据 小结 需求 我的文章 《C# 结合JavaScript实现手写板签名并上传到服务器》主要介绍了 web 版的需求实现,本文应项目需求介绍如何通过 C# WinForm 通过画布画笔…...

GC1272替代APX9172/茂达中可应用于电脑散热风扇应用分析
在电脑散热风扇应用中,选择合适的驱动器件对于风扇的性能和效率至关重要。以下是对GC1272替代APX9172/茂达在此类应用中的分析: 1. 功能比较 GC1272: 主要用于驱动直流风扇,具有高效的电流控制和调速功能。支持PWM调速࿰…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...
