深度学习——线性神经网络(三、线性回归的简洁实现)
目录
- 3.1 生成数据集
- 3.2 读取数据集
- 3.3 定义模型
- 3.4 初始化模型参数
- 3.5 定义损失函数
- 3.6 定义优化算法
- 3.7 训练
在上一节中,我们通过张量来自定义式地进行数据存储和线性代数运算,并通过自动微分来计算梯度。实际上,由于数据迭代器、损失函数、优化器和神经网络层很常用,现代深度学习框架已经为我们实现了这些组件,只需要调用即可。
3.1 生成数据集
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2ltrue_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b,1000)
# 可以打印出来看一下
print(features,labels)

3.2 读取数据集
我们可以通过调用框架中现有的API来读取数据,将features和labels作为API的参数传递,并通过数据迭代器指定batch_size,此外,布尔值is_train表示是否希望数据迭代器对象在每轮内打乱数据。
def load_array(data_arrays, batch_size, is_train=True):"""构造一个Python数据迭代器"""dataset = data.TensorDataset(*data_arrays)return data.DataLoader(dataset, batch_size, shuffle=is_train)batch_size = 10
data_iter = load_array((features,labels), batch_size)
提到的data.TensorDataset(*data_arrays)中,*号的用法与函数定义中的类似,它表示TensorDataset可以接受任意数量的参数。这些参数通常是torch.Tensor对象,其中最后一个参数默认被视为标签,其余的参数被视为特征。
使用iter函数构造Python迭代器,并使用next函数从迭代器中获取第一项。
print(next(iter(data_iter)))
我是用pycharm写的代码,和jupyter中有些不一样,jupyter中直接写next(iter(data_iter))就可以打印出来了,pycharm中必须要加上print

因为布尔值shuffle=is_train表示数据迭代器对象在每轮内打乱数据,所以next函数取出来的第一批量10项数据,并不直接是生成的数据集中的前10项数据。这点大家可以注意一下!
3.3 定义模型
对于标准深度学习模型,我们可以使用框架已经预定义好的层,这使我们只需关注使用哪些层来构造模型,而不必关注层的实现细节。
我们先定义一个模型变量net,它是一个Sequential类的实例。Sequential类将多个层串联在一起,当给定输入数据时,Sequential实例将数据传入第一层,然后将第一层的输出作为第二层的输入,以此类推。
在线性神经网络中,模型只包含一个层,因此实际上不需要Sequential,但是由于以后几乎所有的模型都是多个层的,在这里使用Sequential类更方便理解“标准的流水线”。

在单层网络架构中,这一单层称为“全连接层”,因为它的每个输入都通过矩阵-向量乘法得到它的每个输出。
在pytorch中,全连接层在Linear类中定义,我们将两个参数传递到nn.Linear中,第一个参数指定输入特征的形状,即2;第二个参数指定输出特征形状,输出特征形状为单个标量,因此为1。
# nn是神经网络的缩写
from torch import nnnet = nn.Sequential(nn.Linear(2,1))
3.4 初始化模型参数
在使用net之前,我们需要初始化模型参数,如在线性回归模型中的权重和偏置。深度学习框架通常由预定义的方法来初始化参数。
在这里,我们指定每个权重系数应该从均值为0,标准差为0.01的正态分布中随机抽样,偏置参数将初始化为0.
我们在构造nn.Linear时指定了输入和输出的尺寸,现在可以直接访问参数以设定它们的初始值。通过net[0]选择网络中的第一层,然后使用weight.data和bias.data方法访问函数。我们还可以使用替换方法normal_和fill_来重写参数值。
# 重写参数值之前的对比
print(net[0].weight.data)
print(net[0].bias.data)net[0].weight.data.normal_(0,0.01)
net[0].bias.data.fill_(0)
print(net[0].weight.data)
print(net[0].bias.data)
下面是重写参数值之前的对比
3.5 定义损失函数
计算均方误差使用的是MSELoss类,也称为平方 L 2 L_2 L2范数。默认情况下,它返回所有样本损失的平均值
loss = nn.MSELoss()
3.6 定义优化算法
小批量随机梯度下降算法是一种优化神经网络的标准工具,Pytorch在optim模块中实现了该算法的许多变体。当我们实例化一个SGD实例时,我们要指定优化的参数(可以通过net.parameters()从我们的模型中获得)以及优化算法所需的超参数字典。小批量随机梯度下降只需要设置lr的值,这里设置为0.03.
trainer = torch.optim.SGD(net.parameters(), lr=0.03)
3.7 训练
在每轮里,我们将完整遍历一次数据集(train_data),不断地从中获取一个小批量的输入和相应的标签。对于每个小批量,将执行以下步骤:
- 通过调用net(X)生成预测并计算损失l(前向传播)
- 通过反向传播来计算梯度
- 通过调用优化器来更新模型参数
为了 更好地度量训练效果,我们计算每轮后的损失,并打印出来监控训练过程。
num_epochs = 3
for epoch in range(num_epochs):for X, y in data_iter:l = loss(net(X), y)trainer.zero_grad()l.backward()trainer.step()l = loss(net(features),labels)print(f'epoch{epoch + 1}, loss {l:f}')

几点注意:
l = loss(net(X), y)
loss函数中已经有了sum()操作,省略了原来实现过程中的 l.sum() 这一步骤
net(X)
net()本身就带了模型中的参数,就不需要把W,b写进去了
trainer.zero_grad()
优化器需要先把梯度清零
trainer.step()
调用step()函数进行模型更新
l = loss(net(features),labels)
模型参数更新完之后,再计算一遍均方误差
下面比较一下生成数据集的真实参数和通过有限数据训练获得的模型参数。要访问参数,我们首先从net访问所需的层,然后读取该层的权重和偏置。如下所示,我们估计得到的参数与生成数据集的真实参数非常接近。
w = net[0].weight.data
print('w的估计误差:', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差:', true_b - b)

小结:
- 我们可以使用Pytorch中的高级API更简洁地实现模型;
- 在Pytorch中,data模块提供了数据处理工具,nn 模块定义了大量的神经网络层和常见的损失函数;
- 我们可以通过以"_"结尾的方法将参数替换,从而自定义初始化参数。
以下是完整代码:
import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l
# nn是神经网络的缩写
from torch import nntrue_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b,1000)
# 可以打印出来看一下
# print(features,labels)def load_array(data_arrays, batch_size, is_train=True):"""构造一个Python数据迭代器"""dataset = data.TensorDataset(*data_arrays)return data.DataLoader(dataset, batch_size, shuffle=is_train)batch_size = 10
data_iter = load_array((features,labels), batch_size)
# print(next(iter(data_iter)))net = nn.Sequential(nn.Linear(2,1))# 重写参数值之前的对比
# print(net[0].weight.data)
# print(net[0].bias.data)net[0].weight.data.normal_(0,0.01)
net[0].bias.data.fill_(0)
# print(net[0].weight.data)
# print(net[0].bias.data)
loss = nn.MSELoss()trainer = torch.optim.SGD(net.parameters(), lr=0.03)num_epochs = 3
for epoch in range(num_epochs):for X, y in data_iter:l = loss(net(X), y)trainer.zero_grad()l.backward()trainer.step()l = loss(net(features),labels)# print(f'epoch{epoch + 1}, loss {l:f}')w = net[0].weight.data
print('w的估计误差:', true_w - w.reshape(true_w.shape))
b = net[0].bias.data
print('b的估计误差:', true_b - b)
相关文章:

深度学习——线性神经网络(三、线性回归的简洁实现)
目录 3.1 生成数据集3.2 读取数据集3.3 定义模型3.4 初始化模型参数3.5 定义损失函数3.6 定义优化算法3.7 训练 在上一节中,我们通过张量来自定义式地进行数据存储和线性代数运算,并通过自动微分来计算梯度。实际上,由于数据迭代器、损失函数…...

本地部署 Milvus
本地部署 Milvus 1. Install Milvus in Docker2. Install Attu, an open-source GUI tool 1. Install Milvus in Docker curl -sfL https://raw.githubusercontent.com/milvus-io/milvus/master/scripts/standalone_embed.sh -o standalone_embed.shbash standalone_embed.sh …...

Git基础-配置http链接的免密登录
问题描述 当我们在使用 git pull 或者 git push 进行代码拉取或代码提交时, 若我们的远程代码仓库是 http协议的链接时,就是就会提示我们进行账号密码的登录。 每次都要登录,这未免有些麻烦。 本文介绍一下免密登录的配置。解决方案 1 执行…...
)
华为OD机试真题-编码能力提升-2024年OD统一考试(E卷)
最新华为OD机试考点合集:华为OD机试2024年真题题库(E卷+D卷+C卷)_华为od机试题库-CSDN博客 每一题都含有详细的解题思路和代码注释,精编c++、JAVA、Python三种语言解法。帮助每一位考生轻松、高效刷题。订阅后永久可看,持续跟新。 题目描述 为了提升软件编码能力,小…...
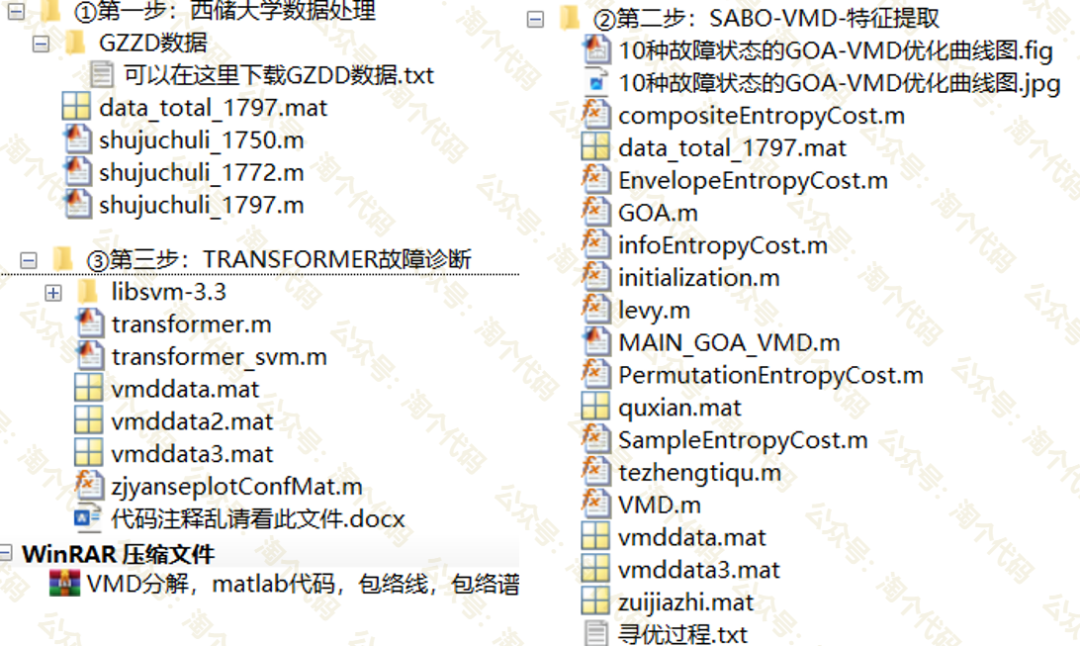
高被引算法GOA优化VMD,结合Transformer-SVM的轴承诊断,保姆级教程!
本期采用2023年瞪羚优化算法优化VMD,并结合Transformer-SVM实现轴承诊断,算是一个小创新方法了。需要水论文的童鞋尽快! 瞪羚优化算法之前推荐过,该成果于2023年发表在计算机领域三区SCI期刊“Neural Computing and Applications”…...

半小时速通RHCSA
1-7章: #01创建以上目录和文件结构,并将/yasuo目录拷贝4份到/目录下 #02查看系统合法shell #03查看系统发行版版本 #04查看系统内核版本 #05临时修改主机名 #06查看系统指令的查找路径 #07查看passwd指令的执行路径 #08为/yasuo/ssh_config文件在/mulu目录下创建软链…...

人工智能和机器学习之线性代数(一)
人工智能和机器学习之线性代数(一) 人工智能和机器学习之线性代数一将介绍向量和矩阵的基础知识以及开源的机器学习框架PyTorch。 文章目录 人工智能和机器学习之线性代数(一)基本定义标量(Scalar)向量&a…...

STM32外设应用详解
STM32外设应用详解 STM32微控制器是意法半导体(STMicroelectronics)推出的一系列基于ARM Cortex-M内核的高性能、低功耗32位微控制器。它们拥有丰富的外设接口和功能模块,可以满足各种嵌入式应用需求。本文将详细介绍STM32的外设及其应用&am…...
优化配置)
docker详解介绍+基础操作 (三)优化配置
1.docker 存储引擎 Overlay: 一种Union FS文件系统,Linux 内核3.18后支持 Overlay2:Overlay的升级版,docker的默认存储引擎,需要磁盘分区支持d-type功能,因此需要系统磁盘的额外支持。 关于 d-type 传送…...

细说Qt的状态机框架及其用法
文章目录 使用场景基本用法状态定义添加转换历史状态QStateMachine是Qt框架中用于构建状态机的一个类,它属于Qt的状态机框架(State Machine Framework)。这个框架提供了一种模型,用于设计响应不同事件(如用户输入、文件I/O或网络活动)的应用程序的行为。通过使用状态机,开发…...

Oracle-表空间与数据文件操作
目录 1、表空间创建 2、表空间修改 3、数据文件可用性切换操作 4、数据文件和表空间删除 1、表空间创建 (1)为 ORCL 数据库创建一个名为 BOOKTBS1 的永久表空间,数据文件为d:\bt01.dbf ,大小为100M,区采用自动扩展…...

C# WinForm实现画笔签名及解决MemoryBmp格式问题
目录 需求 实现效果 开发运行环境 设计实现 界面布局 初始化 画笔绘图 清空画布 导出位图数据 小结 需求 我的文章 《C# 结合JavaScript实现手写板签名并上传到服务器》主要介绍了 web 版的需求实现,本文应项目需求介绍如何通过 C# WinForm 通过画布画笔…...

GC1272替代APX9172/茂达中可应用于电脑散热风扇应用分析
在电脑散热风扇应用中,选择合适的驱动器件对于风扇的性能和效率至关重要。以下是对GC1272替代APX9172/茂达在此类应用中的分析: 1. 功能比较 GC1272: 主要用于驱动直流风扇,具有高效的电流控制和调速功能。支持PWM调速࿰…...

《Linux从小白到高手》综合应用篇:详解Linux系统调优之服务器硬件优化
List item 本篇介绍Linux服务器硬件调优。硬件调优主要包括CPU、内存、磁盘、网络等关键硬件组。 1. CPU优化 选择适合的CPU: –根据应用需求选择多核、高频的CPU,以满足高并发和计算密集型任务的需求。CPU缓存优化: –确保CPU缓存&#x…...
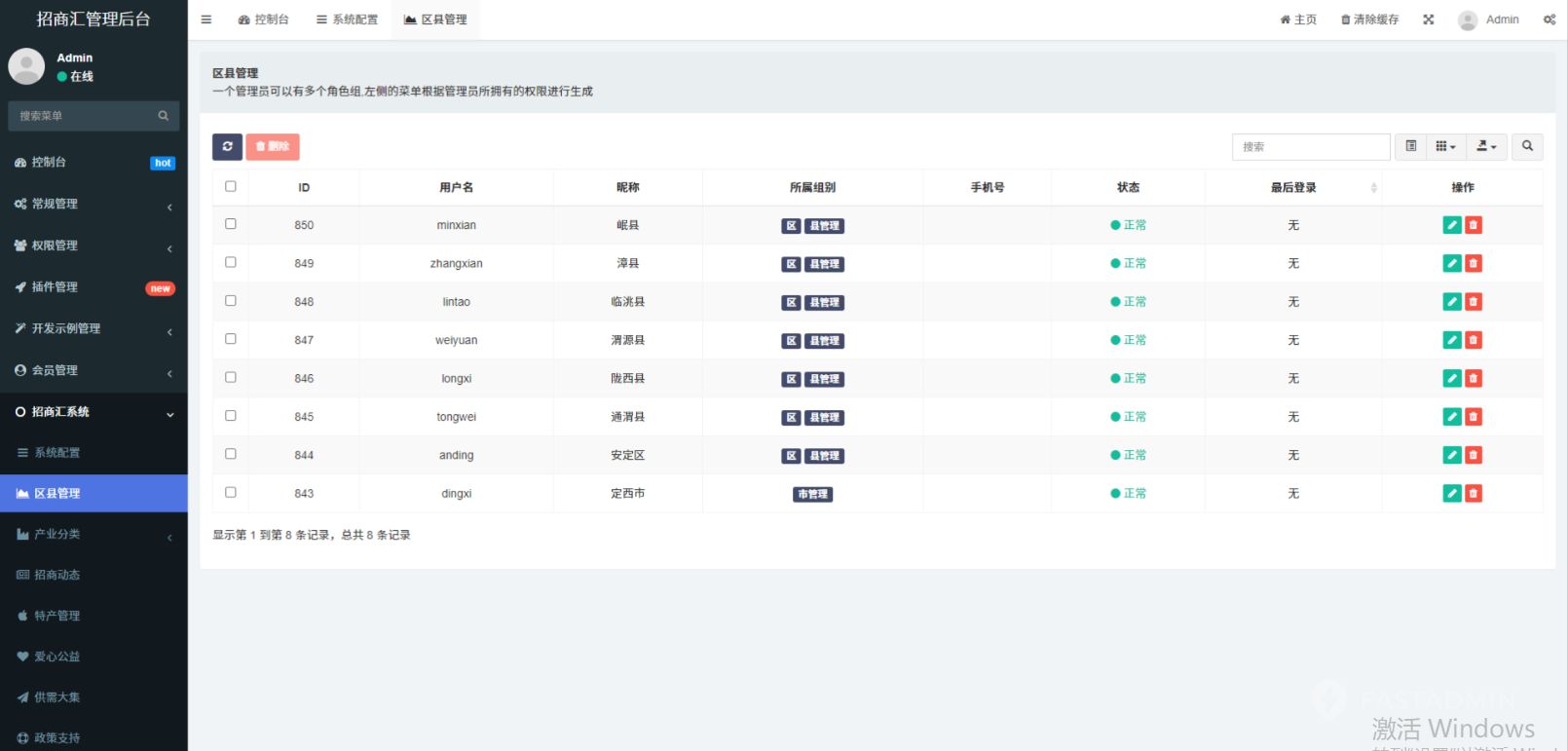
PHP政务招商系统——高效连接共筑发展蓝图
政务招商系统——高效连接,共筑发展蓝图 🏛️ 一、政务招商系统:开启智慧招商新篇章 在当今经济全球化的背景下,政务招商成为了推动地方经济发展的重要引擎。而政务招商系统的出现,更是为这一进程注入了新的活力。它…...
Linux 命令行
这学期是我第一次正式学习 linux ,是在 VMware 里创建了 openEuler 的虚拟机练习 linux 的常用命令。 目前主要在学习 linux 的常用命令,因此这篇博客主要介绍一些常用的命令。 本文将持续更新… 阅读建议 Linux 是一个倒置的树结构(文件系…...

每日一题:单例模式
每日一题:单例模式 ❝ 单例模式是确保一个类只有一个实例,并提供一个全局访问点 1.饿汉式(静态常量) 特点:在类加载时就创建了实例。优点:简单易懂,线程安全。缺点:无论是否使用&…...

前端_001_html扫盲
文章目录 概念标签及属性常用全局属性head里常用标签body里常用标签表情符号 url编码 概念 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>Title</title> </head> <body></bod…...

49 | 桥接模式:如何实现支持不同类型和渠道的消息推送系统?
上一篇文章我们学习了第一种结构型模式:代理模式。它在不改变原始类(或者叫被代理类)代码的情况下,通过引入代理类来给原始类附加功能。代理模式在平时的开发经常被用到,常用在业务系统中开发一些非功能性需求…...

使用js和canvas实现简单的网页贪吃蛇小游戏
玩法介绍 点击开始游戏后,使用键盘上的↑↓←→控制移动,吃到食物增加长度,碰到墙壁或碰到自身就游戏结束 代码实现 代码比较简单,直接阅读注释即可,复制即用 <!DOCTYPE html> <html lang"en"…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

深入浅出WebGL:在浏览器中解锁3D世界的魔法钥匙
WebGL:在浏览器中解锁3D世界的魔法钥匙 引言:网页的边界正在消失 在数字化浪潮的推动下,网页早已不再是静态信息的展示窗口。如今,我们可以在浏览器中体验逼真的3D游戏、交互式数据可视化、虚拟实验室,甚至沉浸式的V…...

用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法
用神经网络读懂你的“心情”:揭秘情绪识别系统背后的AI魔法 大家好,我是Echo_Wish。最近刷短视频、看直播,有没有发现,越来越多的应用都开始“懂你”了——它们能感知你的情绪,推荐更合适的内容,甚至帮客服识别用户情绪,提升服务体验。这背后,神经网络在悄悄发力,撑起…...
进行稀疏数据预测的技术方案)
结合PDE反应扩散方程与物理信息神经网络(PINN)进行稀疏数据预测的技术方案
以下是一个结合PDE反应扩散方程与物理信息神经网络(PINN)进行稀疏数据预测的技术方案,包含完整数学推导、PyTorch/TensorFlow双框架实现代码及对比实验分析。 基于PINN的反应扩散方程稀疏数据预测与大规模数据泛化能力研究 1. 问题定义与数学模型 1.1 反应扩散方程 考虑标…...
