github pages + hugo 搭建静态博客网站
体验地址
1. 起因, 目的:
-
其实6年前,我就写过这个。
项目代码
博客地址 -
最近想改写一下。
github 推荐的主题是 Jekyll, 我当时用的就是这个,感觉很麻烦。尤其是文章命名。 -
新的主题 hugo 用起来还行。
2.过程:
过程记录, 需要详细! 因为问题非常多!
3. 参考教程:
- 视频教程: https://www.youtube.com/watch?v=_QSr2_pxIJs
- 配置文件,参考来源: https://theplaybook.dev/docs/deploy-hugo-to-github-pages/
一句话介绍 hugo:
hugo 是一个静态博客渲染工具, go 语言写的。
安装:
choco install hugo-extended # 失败。 估计是权限
scoop install hugo-extended # ok!
运行的话, 最好是使用 wsl , cmd 也行!!
新 hugo 建项目
hugo new site my_hugo_blog -f yaml
cd my_hugo_blog
安装主题,
git init
git clone https://github.com/adityatelange/hugo-PaperMod themes/PaperMod --depth=1
git submodule add --depth=1 https://github.com/adityatelange/hugo-PaperMod.git themes/PaperMod
修改 “hugo.toml”, 增加一行
theme = “PaperMod”
新建文章
hugo new docs/test_file.md
!!! !!! !!! !!!
!!! 修改 draft = true, ----> draft = false 否则无法渲染。 直接删掉这一行也行。
!! !!! !!! !!!
查看文章: localhost:7897/docs/test_file
下面就 github 相关的操作了
- 创建github 项目,上传文件。
- 新建一个分支, gh-pages !!! 这里名称不能变。 必须是 gh! 一个字都不能变!
- 开启 github actions 读写权限 https://github.com/buxuele/my_hugo_blog/settings/actions
- mkdir -p .github/workflows, 新建+修改 deploy.yml
- 修改 “hugo.toml”, 增加 baseUrl
报错:
其实就是修改一个 hugo 的版本。
老哥留步,支持一下。

相关文章:

github pages + hugo 搭建静态博客网站
体验地址 1. 起因, 目的: 其实6年前,我就写过这个。 项目代码 博客地址 最近想改写一下。 github 推荐的主题是 Jekyll, 我当时用的就是这个,感觉很麻烦。尤其是文章命名。 新的主题 hugo 用起来还行。 2.过程: 过程记录&am…...

Python爬虫如何爬取并解析JSON数据
前言 Python爬虫是一种用于从互联网上获取数据的程序,而JSON(JavaScript Object Notation)是一种常用的数据交换格式。本文将介绍如何使用Python爬虫来爬取并解析JSON数据,同时还会讲解如何使用代理IP来提高爬取效率。 1. 什么是…...

【C++】精妙的哈希算法
🚀个人主页:小羊 🚀所属专栏:C 很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~ 目录 一、哈希结构1、哈希概念2、哈希函数3、哈希冲突3.1 闭散列3.2 开散列 4、完整代码 一、哈希结构 1、哈希概念 A…...

智慧链动青春:国家区块链中心接待北京市十一学校青少年访学探索
以生动科学的方法点燃青少年科学探索欲望是构建未来科技人才梯队的基石。近期国家区块链技术创新中心接待北京市十一学校新生访学,以科普讲座、实操互动的方式让学生在深度思考中感受科学魅力、接触前沿科技,激发学生对区块链、隐私计算和芯片设计制造的…...

利用C++封装鼠标轨迹算法为DLL:游戏行为检测的利器
在现代软件开发中,鼠标轨迹模拟技术因其在自动化测试、游戏脚本编写等领域的广泛应用而备受青睐。本文将介绍如何使用C语言将鼠标轨迹算法封装为DLL(动态链接库),以便在多种编程环境中实现高效调用,同时探讨其在游戏行…...

Qt- QSS风格选择器常用属性选择器样式表盒子
1. 风格设置 Qt 提供了 3 种整体风格,使用 QStyleFactory::keys() 来获取 (windowsvista 、Windows 、Fusion) 可以在 main.cpp 中调用 setStyle 方法对应用程序进行全局风格的设置 int main(int argc, char *argv[]) {QApplication a(arg…...

粤智助自助一体机大厂浮出水面 OBOO鸥柏已成服务终端中坚力量
自助服务查询一体机作为操作自主化便民的重要窗口,OBOO鸥柏自助服务终端机以其显著的技术优化,通过触摸屏或其他交互界面,使用户能够自助服务完成各种操作,如支付、查询信息终端、办理业务,自助查档答应一体化等。为交…...

SpringBoot-application.properties配置
默认配置最终都是映射/关联到某个类 #SPRING CONFIG(ConfigFileApplicationListener) spring.config.name #配置文件名(默认 为 application ) spring.config.location #配置文件的位置 …...

STM32-ADC模数转换
一、概述 ADC(Analog-Digital Converter)模拟-数字转换器 ADC可以将引脚上连续变化的模拟电压转换为内存中存储的数字变量,建立模拟电路到数字电路的桥梁12位逐次逼近型ADC,1us转换时间输入电压范围:0~3.3Vÿ…...

lspci | grep VGA
执行lspci | grep VGA后如下,解释含义 00:0f.0 VGA compatible controller: VMware SVGA II Adapter 0b:00.0 VGA compatible controller: NVIDIA Corporation GA104 [GeForce RTX 3070] (rev a1) 执行 lspci | grep VGA 命令后,您得到了两条输出&#…...

智慧厂区车辆导航解决方案;智慧工厂电子地图应用解决方案;大型工厂内部导航解决方案;智慧工厂可视化地图应用方案
智慧厂区车辆导航解决方案;智慧工厂电子地图应用解决方案 在智慧工业的蓬勃发展背景下,上海懒图科技凭借其室内电子地图技术的深厚积淀,正为智慧工厂物流管理领域注入革新力量。其创新的车辆导航与可视化管理系统,凭借高精度定位…...

决策树C4.5算法详解及实现
C4.5决策树是一种广泛使用的机器学习算法,它用于分类任务。它是在ID3算法的基础上改进的,主要通过生成决策树来构建分类模型。C4.5通过以下步骤工作: 1. 数据集分裂 C4.5通过选择具有最高信息增益率的特征来分裂数据集。信息增益率…...

prompt learning
prompt learning 对于CLIP(如上图所示)而言,对其prompt构造的更改就是在zero shot应用到下游任务的时候对其输入的label text进行一定的更改,比如将“A photo of a{obj}”改为“[V1][V2]…[Vn][Class]”这样可学习的V1-Vn的token…...

适用于 Windows 11 的 5 大数据恢复软件 [免费和付费]
为什么我们需要Windows 11数据恢复软件? 计算机用户经常遇到的一件事就是数据丢失,这种情况随时可能发生。错误地删除重要文件和文件夹可能会非常令人担忧,但幸运的是,有一种方法可以恢复 PC 上丢失的数据。本文将向您展示可用于…...

vue实现获取当前时间并实时显示
以下代码可以实现获取当前时间并实时显示,朋友们直接copy使用即可,希望可以帮助到有需要的朋友们! <template><div class"time">{{ datetimeStr }}</div> </template> <script>export default {data…...
【论文阅读】SRCNN
学习资料 论文题目:Learning a Deep Convolutional Network for Image Super-Resolution(学习深度卷积网络用于图像超分辨率)论文地址:link.springer.com/content/pdf/10.1007/978-3-319-10593-2_13.pdf代码:作者提出的…...

数据结构与算法——Java实现 32.堆
目录 堆 大顶堆 威廉姆斯建堆算法 Floyd建堆算法 Floyd建堆算法复杂度 大顶堆代码实现 人的想法和感受是会随着时间的认知改变而改变, 原来你笃定不会变的事,也会在最后一刻变得释然 —— 24.10.10 堆 堆是基于二叉树实现的数据结构 大顶堆任意一个父节…...
)
深度学习 .dot()
在 MXNet 中,.dot() 是用于计算两个数组的点积(矩阵乘法)的方法。这个方法适用于一维和二维数组,并返回它们的点积结果。 语法 ndarray1.dot(ndarray2) 参数 ndarray1: 第一个输入数组。ndarray2: 第二个输入数组,…...
idea2024 git merge 时丢失 Merge remote-tracking branch问题
idea2024 git merge 时丢失 Merge remote-tracking branch问题 处理建议 直接修改本地git的配置 git config --global merge.ff false 分析 在 IntelliJ IDEA 中进行 Git merge 操作时,有时你可能会遇到提交历史中丢失 Merge remote-tracking branch 的信息&#…...
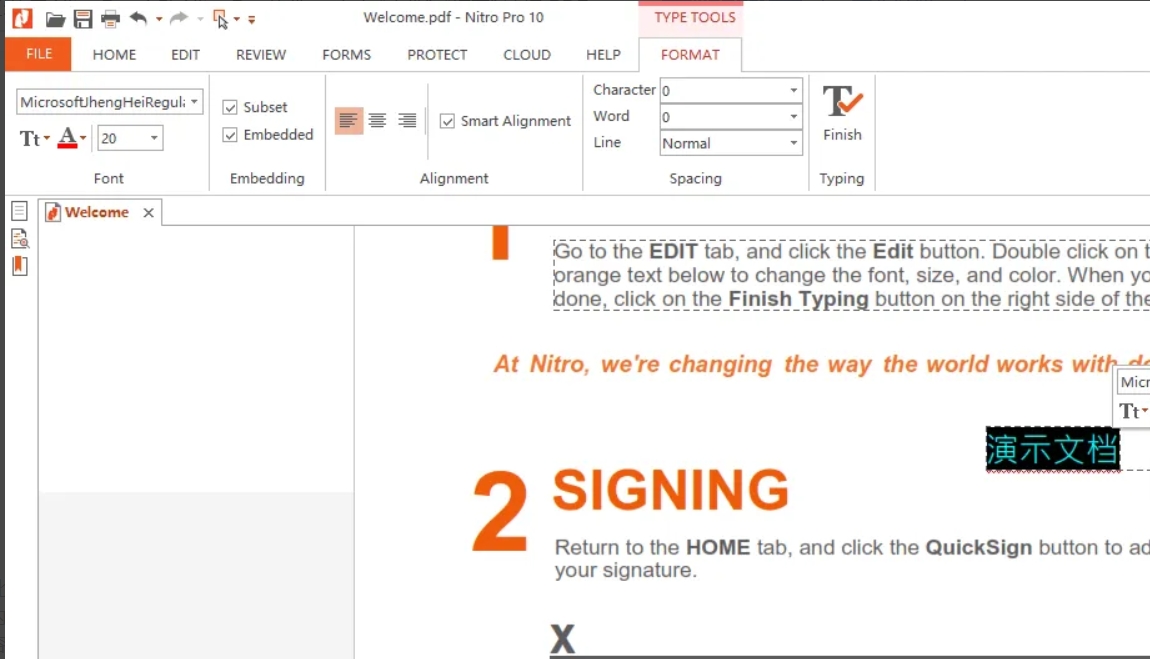
pdf怎么删除多余不想要的页面?删除pdf多余页面的多个方法
pdf怎么删除多余不想要的页面?在日常办公或学习中,我们经常会遇到需要处理PDF文件的情况。PDF文件因其格式稳定、不易被篡改的特点而广受青睐,但在编辑方面却相对不如Word等文档灵活。有时,在接收或创建的PDF文件中,可…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
