【STL】AVLTree模拟实现
AVLTree模拟实现
- 1 前言
- 2 AVL树的插入
- 2.1 平衡因子不继续向上更新的情况
- 2.2 平衡因子变为2或者-2,发生旋转
- 2.2.1 左单旋
- 2.2.2 右单旋
- 2.2.3 左右双旋
- 2.2.4 右左双旋
- 3 代码
1 前言
二叉搜索树的不足:如果出现极端情况,效率会变得很低。
AVL:二叉平衡搜索树
平衡因子:右子树的高度 - 左子树的高度 平衡因子绝对值不超过1(-1, 0, 1)
1.平衡因子为什么不是0?而是 -1, 0 ,1??
做不到,两个节点的时候不能相等,四个节点也做不到
AVL树的效率:
增删查改:高度次 O(log N)
满二叉树:2^h - 1 = N
AVL树:2^h - x = N
x的范围:[1, 2^(h - 1) - 1]
2 AVL树的插入
2.1 平衡因子不继续向上更新的情况
插入的原则:
新增在左:parent的平衡因子–
新增在右:parent的平衡因子++


从这里可以看出,当平衡因子的值为 -1 或者 1 的时候,并不会停止向上更新。
只有当平衡因子更新为0的时候,才不会继续往上更新了。
2.2 平衡因子变为2或者-2,发生旋转

当平衡因子的值更新为 -2或者2的时候,就代表这棵树不平衡了,就需要进行旋转。这时候更新也停止了(因为要进行旋转了)
2.什么情况要继续往上更新?(更新结束的条件)
更新后的parent平衡因子==0,说明parent所在的子树的高度不变,不会再影响祖先,不用再继续往上更新
更新后的parent平衡因子 ==1 或者 -1,说明parent所在的子树的高度发生改变,会影响祖先,要继续往上更新
更新后的parent平衡因子 ==2 或者 -2,说明parent所在的子树的高度发生改变且不平衡,想办法调整平衡(对parent所在子树进行旋转,让他平衡)
更新到根节点 --> 更新结束
2.2.1 左单旋
发生左单旋的情况:(具体图,某一种情况)

发生左单旋的抽象图(有很多种情况):

什么情况会发生左单旋?
在右边高的情况下往右边插入。
转化成代码就是:在插入之后,
parent->_bf = 2 && cur->_bf = 1.这里parent->_bf = 2说明是右边高,如果parent->_bf = -2,说明是左边高。
总结:
cur->left 比 parent大,所以,cur->left做parent的右没有问题
cur->left比cur小,所以,cur->left做cur的左没有问题
核心操作:
parent->right = cur->left
cur->left = parent;
2.2.2 右单旋
发生右单旋的情况(具体图):

发生右单旋的抽象图(有很多种情况):

旋转:
右边高 --> 往左边旋转
左边高 --> 往右边旋转
旋转的时候要注意的问题:
- 保持他是搜索树
- 变成平衡树且降低这个子树的高度
2.2.3 左右双旋
左右双旋的情况:
当父节点左边高并且当前节点的右边高时,就会发生左右双旋。

双旋平衡因子的更新:
区分的关键,看插入节点的父节点的平衡因子
平衡因子的三种情况:h == 0, h > 0。h > 0又分为两种情况:插入节点是父节点的左子树或者插入节点是父节点的右子树
2.2.4 右左双旋
右左双旋:
当父节点的右边高并且当前节点的左边高时,就会发生右左双旋


如何分清是单旋还是双旋?
单旋:单纯的一边高,左边高或者右边高
双旋:有折现的产生。
3 代码
AVLTree.h
#pragma once
#include <iostream>
#include <assert.h>
using namespace std;template <class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;//new一个AVLTreeNode节点的时候就会调用这个构造函数// 如果传入参数,就是kvAVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};template <class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){//搜索的插入//...控制平衡//新增在左边,父节点的平衡因子-- | 新增在右边,父节点的平衡因子++ 新增的节点会影响到它的祖先if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{assert("插入相同的节点");}}//走到这里,找到了要插入的位置 --> 将cur插入进去cur = new Node(kv);if (cur->_kv.first < parent->_kv.first)parent->_left = cur;elseparent->_right = cur;//因为是三叉链,所以cur的_parent指针还要指回去cur->_parent = parent;//走到这里,插入完成了。需要检查平衡因子,判断是否平衡,不平衡要进行旋转while (parent){//插入的位置是左孩子,bf--;插入的位置是右孩子,bf++if (cur == parent->_left)parent->_bf--;elseparent->_bf++;//接下来要判断根据不同的平衡因子进行不同的更新的情况if (parent->_bf == 0){break; //如果是0, 就不用更新了}else if (parent->_bf == -1 || parent->_bf == 1) //如果插入之后parent的平衡因子等于-1或者1,说明还要向上调整{cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//如果平衡因子走到这里,说明要发生旋转了:左旋,右旋,双旋。if (parent->_bf == 2 && cur->_bf == 1){//这种情况是左单旋,为什么?RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){//左边高,还要往左边插入,所以要发生右单旋RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){//父节点右边高,当前节点左边高 --> 右左双旋RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){//父节点左边高,当前节点右边高 --> 左右双旋RotateLR(parent);}else{assert("平衡因子出错");}break;}else{assert("平衡因子出错");}}return true;}void RotateL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;//1.把curleft给parent的right --> parent的_right指向curleftparent->_right = curleft;//判断curleft是否为空,如果不为空,就curleft的父节点指回去if (curleft){curleft->_parent = parent;}//2.parent的right给cur的left --> cur的_left指向parentcur->_left = parent;//3.判断parent是不是当前的根节点,如果是,cur的_parent就为空。如果不是,cur的_parent还要指向ppnodeNode* ppnode = parent->_parent;//4.parent还要往回指,因为是三叉链parent->_parent = cur;if (parent == _root) //如果是根节点{_root = cur;cur->_parent = nullptr;}else{//如果不是根节点,就要判断是ppnode的左孩子还是右孩子if (ppnode->_left == parent)ppnode->_left = cur;elseppnode->_right = cur;//往回指cur->_parent = ppnode;}//更新平衡因子parent->_bf = cur->_bf = 0;}void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;//1.让parent的左指向cur的右parent->_left = curright;if (curright){//第一次往回指curright->_parent = parent;}//找到parent的父节点Node* ppnode = parent->_parent;//2.cur的右指向parentcur->_right = parent;//第二次往回指parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{parent->_parent = cur;if (ppnode->_left == parent)ppnode->_left = cur;elseppnode->_right = cur;//第三次往回指cur->_parent = ppnode;}//更新平衡因子cur->_bf = parent->_bf = 0;}//左右双旋void RotateLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(cur);RotateR(parent);//根据不同的情况修改平衡因子if (bf == 0){cur->_bf = 0;parent->_bf = 0;curright->_bf = 0;}else if (bf == 1) //说明左边低,右边高{parent->_bf = 0;cur->_bf = -1;curright->_bf = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}else{assert("RotateLR false");}}void RotateRL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf; //提前保存下来RotateR(cur);RotateL(parent);if (bf == 0){cur->_bf = 0;parent->_bf = 0;curleft->_bf = 0;}else if (bf == 1) //说明插入的位置是curleft的右边{parent->_bf = -1;cur->_bf = 0;curleft->_bf = 0;}else if (bf == -1) //插入的位置是curleft的左边{parent->_bf = 0;cur->_bf = 1;curleft->_bf = 0;}else{assert("RotateRL false");}}//bool Erase(const pair<K, V>& key)//{//}int Height(){return Height(_root);}int Height(Node* root){if (root == nullptr)return 0;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr)return true;int leftHight = Height(root->_left);int rightHight = Height(root->_right);if (rightHight - leftHight != root->_bf){cout << "平衡因子异常:" << root->_kv.first << "->" << root->_bf << endl;return false;}return abs(rightHight - leftHight) < 2&& IsBalance(root->_left)&& IsBalance(root->_right);}void Inorder(){_Inorder(_root);}private:void _Inorder(Node* cur){if (cur == nullptr)return;_Inorder(cur->_left);cout << cur->_kv.first << " : " << cur->_kv.second << " : " << cur->_bf << endl;_Inorder(cur->_right);}
private:Node* _root = nullptr;
};Test_AVLTree.cpp
#include "AVLTree.h"void testAVL1()
{int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };AVLTree<int, int> t;for (auto e : a){t.Insert(make_pair(e, e));}t.IsBalance();t.Inorder();
}int main()
{testAVL1();return 0;
}

相关文章:

【STL】AVLTree模拟实现
AVLTree模拟实现 1 前言2 AVL树的插入2.1 平衡因子不继续向上更新的情况2.2 平衡因子变为2或者-2,发生旋转2.2.1 左单旋2.2.2 右单旋2.2.3 左右双旋2.2.4 右左双旋 3 代码 1 前言 二叉搜索树的不足:如果出现极端情况,效率会变得很低。 AVL&am…...

无极低码课程【tomcat部署windows环境厂家乱码处理】
windows 下tomcat安装 下载地址一:https://tomcat.apache.org/download-90.cgi 下载地址二:https://archive.apache.org/dist/tomcat/ 解压tomcat,进入bin目录运行startup.bat...

注册安全分析报告:惠农网
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞…...

Qualitor checkAcesso.php 任意文件上传漏洞复现(CVE-2024-44849)
0x01 漏洞概述 Qualitor 8.24及之前版本存在任意文件上传漏洞,未经身份验证远程攻击者可利用该漏洞代码执行,写入WebShell,进一步控制服务器权限。 0x02 复现环境 FOFA:app="Qualitor-Web" 0x03 漏洞复现 PoC POST /html/ad/adfilestorage/request/checkAcess…...

PHP-FPM和FastCGI
文章目录 前言一. FastCGI1.定义2.工作方式3.协议4.架构5.工作原理(请求生命周期) 二. PHP-FPM1.定义:2.特性3.进程管理模式4.工作流程 三.关系与应用四.配置示例五.性能优化六.配置选项七.常见问题及解决方案 前言 PHP-FPM 是基于 FastCGI …...

【Linux快速入门(二)】Linux与ROS学习之编译基础(make编译)
目录 零.前置篇章 一.make的由来 二.安装make 三.编写Makefile 四.编译运行 五.删除可执行文件 零.前置篇章 第一篇【Linux快速入门】Linux与ROS学习之编译基础(gcc编译)_linuxros-CSDN博客 一.make的由来 "make"是一个用于自…...

jupyterlab的安装与使用攻略/包括汉化方法
官网链接 Project Jupyter | Home 1.第一步安装 打开控制台 使用pip工具安装 pip install jupyterlab 如图 2.安装成功后启动 jupyter lab 会自动启动它的web页面 然后就可以正常使用咯!! 如果需要更换浏览器访问 新开控制台执行下面命令 jupy…...

std::list
std::list是C标准库中的一个序列容器,它提供了双向链表的功能。std::list允许在序列的任何位置高效地插入和删除元素,而不会引起其他元素的移动,这使得std::list在需要频繁插入和删除操作的场景中非常有用。 std::list的特性: 双…...

opencv-rust 系列2: camera_calibration
opencv-rust 系列2: camera_calibration 前言: 这里只是opencv-rust自带示例的中文注解. 略微增加了一些代码也是我在调试时用到的. 说明: camera_calibration.rs是opencv-rust自带的示例, 在examples目录中可以找到,我增加了一些中文注释如下.如需运行可以在项目根目录执行命…...

JVM和GC案例详解
接上文JVM环境配置说明:上文博客 一、JVM远程连接设置 1. JMX方式连接(这种方式没有GC监控),设置如下 2. 连接成功后可以查看基础配置参数(和服务器配置一致) 2. jstatd方式连接(这种方式没有CPU监控) 添加jstatd方式连接 双击Tomcat࿰…...

postgreSql下载安装
一、下载 官网:PostgreSQL: The worlds most advanced open source database 二、安装 1.找到.exe文件,双击安装 2.跟着安装向导操作 三、启动...
GPT-SOVIT模型部署指南
一、模型介绍 强大的小样本语音转换和文本转语音 WebUI。 具有以下特征: 零样本 TTS: 输入 5 秒的声音样本并体验即时文本到语音的转换。少量样本 TTS: 仅使用 1 分钟的训练数据对模型进行微调,以提高语音相似度和真实感。跨语…...
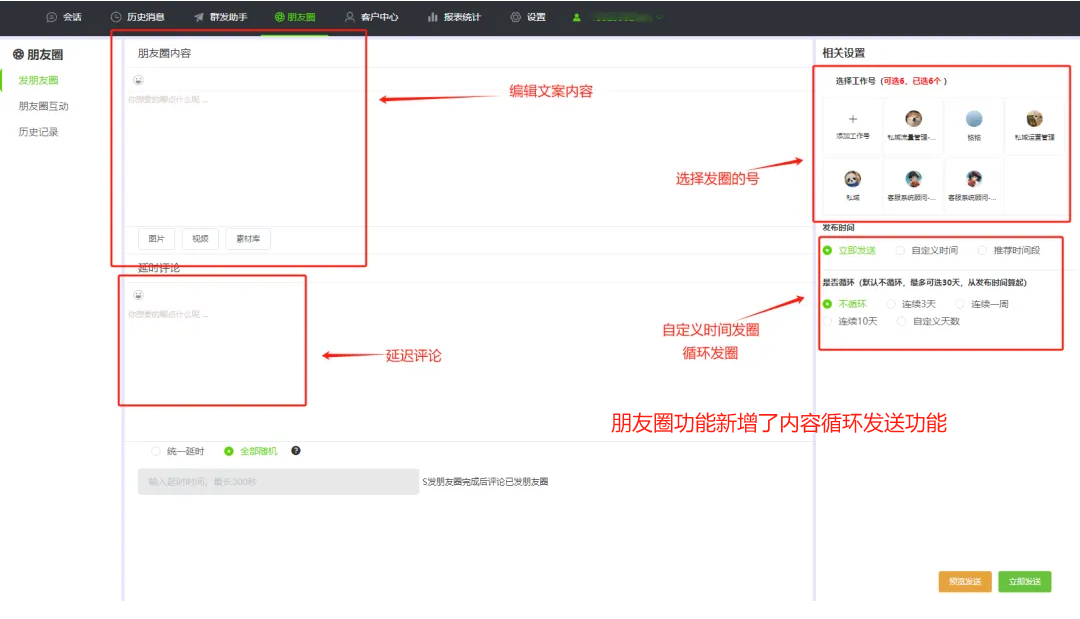
怎么定时发朋友圈?
要实现微信朋友圈的定时发布,可以采用以下几种方法: 1、 绑定QQ号并使用QQ空间定时功能: 于微信和QQ的紧密联系,可以通过绑定QQ号,利用QQ空间的定时发布功能来间接实现微信朋友圈的定时发布。首先,在QQ空…...

如何利用phpstudy创建mysql数据库
phpStudy诞生于2007年,是一款老牌知名的PHP开发集成环境工具,产品历经多次迭代升级,目前有phpStudy经典版、phpStudy V8(2019版)等等,利用phpstudy可以快速搭建一个mysql环境,接下来我们就开始吧…...

五、Linux之Vi和Vim编辑器
基本介绍 Vi Linux 系统会内置 vi 文本编辑 Vim 具有程序编辑的能力,可以看做是 Vi 的增强版本,可以主动的以字体颜色辨别语法的正确性,方便程序设计。 代码补完、编译及错误跳转等方便编程的功能特别丰富 常用的三种模式 正常模式 以 vim …...

git删除错误的commit
文章目录 1、git删除错误的commit2、.gitignore配置文件不生效的问题 1、git删除错误的commit git的流程如图: 当某次失误造成commit的版本有问题,需要回退到正常的版本修改后重新add。 首先通过git log查看commit提交记录,可以看到HEAD-…...

代码随想录算法训练营Day08 | 344.反转字符串、541. 反转字符串II、卡码网:54.替换数字
文章目录 344.反转字符串思路与重点 541. 反转字符串II思路与重点 卡码网:54.替换数字思路与重点 344.反转字符串 题目链接:344. 反转字符串 - 力扣(LeetCode)讲解链接:代码随想录 (programmercarl.com)状态ÿ…...

mysql锁之乐观锁、悲观锁、表锁、行锁、共享锁、排他锁
mysql锁之乐观锁、悲观锁、表锁、行锁、共享锁、排他锁 MySQL锁概述 锁是计算机协调多个进程或线程并发访问某一个资源的机制,在数据库中,除传统的计算资源(CPU、RAM、I/O)的争用以外,数据也是一种供许多用户共享的资…...

【软件干货】Android应用进程如何保活?
1.Android 应用进程保活方法介绍 在Android应用程序中,为了保证应用的正常运行和稳定性,有时需要对应用进程进行保活。以下是一些实现进程保活的方法: 1、使用前台服务(Foreground Service):将服务调用startForeground()方法&…...

neo4j部署保姆级教程
由于公司是基于大数据架构的,让部署neo4j数据库,之前没有接触过,然后紧急学了一下,并且从网上找了一些教程,决定还是记录下来,后续有时间了会在出一篇使用教程 环境准备(root用户) …...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
