Java基础概览和常用知识(七)
什么是自动装箱和自动拆箱,原理是什么?
自动装箱和自动拆箱是Java编程语言中的两个重要概念,它们涉及到基本数据类型与其对应包装类之间的自动转换。
一、定义
自动装箱:是指Java编译器在需要将基本数据类型转换为对应的包装类时,会自动进行转换的过程。例如,将int类型转换为Integer类型,将double类型转换为Double类型等。
自动拆箱:则是自动装箱的逆过程,即Java编译器在需要将包装类对象转换为对应的基本数据类型时,会自动进行转换。例如,将Integer类型转换为int类型,将Double类型转换为double类型等。
二、原理
自动装箱:当基本数据类型被赋值给一个包装类对象时,编译器会自动生成一个调用对应包装类构造函数的代码。这种转换是通过包装类的构造函数或静态工厂方法(例如Integer.valueOf(int i))实现的。
自动拆箱:当包装类对象被赋值给基本数据类型时,编译器会自动生成一个调用包装类的xxxValue()方法的代码,以获取基本数据类型的值。这种转换是通过包装类提供的xxxValue()方法实现的,其中xxx表示基本数据类型(如intValue、doubleValue等)。
三、例子
- 自动装箱:
int num = 5;
Integer numObj = num; // 自动装箱,编译器会将int类型的num自动转换为Integer类型的numObj在这个例子中,编译器将int类型的num自动转换为Integer类型的numObj。
- 自动拆箱:
Integer numObj = 10;
int num = numObj; // 拆箱,编译器会将Integer类型的numObj自动转换为int类型的num在这个例子中,编译器将Integer类型的numObj自动转换为int类型的num。
另外,自动装箱和拆箱在Java集合框架(如ArrayList)中尤为重要,因为这些框架只能存储对象而不能存储基本数据类型。例如:
ArrayList<Integer> list = new ArrayList<>();
list.add(10); // int 10 被自动装箱为 Integer 对象
int value = list.get(0); // Integer 对象被自动拆箱为 int 基本类型在这个例子中,list.add(10)将int类型的10自动装箱为Integer对象,然后list.get(0)将Integer对象自动拆箱为int基本数据类型。
举例:
Integer i = 10; //装箱
int n = i; //拆箱上面这两行代码对应的字节码为:
L1LINENUMBER 8 L1ALOAD 0BIPUSH 10INVOKESTATIC java/lang/Integer.valueOf (I)Ljava/lang/Integer;PUTFIELD AutoBoxTest.i : Ljava/lang/Integer;L2LINENUMBER 9 L2ALOAD 0ALOAD 0GETFIELD AutoBoxTest.i : Ljava/lang/Integer;INVOKEVIRTUAL java/lang/Integer.intValue ()IPUTFIELD AutoBoxTest.n : IRETURN从字节码中,我们发现装箱其实就是调用了 包装类的valueOf()方法,拆箱其实就是调用了 xxxValue()方法。
因此,
Integer i = 10等价于Integer i = Integer.valueOf(10)int n = i等价于int n = i.intValue();
注意:如果频繁拆装箱的话,也会严重影响系统的性能。我们应该尽量避免不必要的拆装箱操作。
private static long sum() {// 应该使用 long 而不是 LongLong sum = 0L;for (long i = 0; i <= Integer.MAX_VALUE; i++)sum += i;return sum;
}总的来说,自动装箱和自动拆箱机制使得Java语言的基本数据类型与对象之间的转换变得更加简单和高效。然而,在使用时也需要注意其潜在的问题,如性能开销和可能的空指针异常等。因此,在编写代码时,应尽量避免在循环或大量计算中自动装箱,如果可能,手动进行装箱操作以减少不必要的开销。
什么浮点数运算的时候会有精度丢失的风险?
浮点数运算时会有精度丢失的风险,这主要源于浮点数在计算机中的表示方式及其运算特性。以下是对这一现象的详细解释:
一、浮点数的表示方式
二进制系统:计算机内部使用二进制系统来存储和处理数据。然而,许多十进制小数在转换为二进制时无法得到一个有限长度的循环小数或终止小数,例如十进制的0.1在二进制中就是无限循环小数。
IEEE 754标准:浮点数在计算机中通常采用IEEE 754标准进行表示,该标准定义了浮点数的编码格式,包括符号位、指数部分和尾数部分。其中,尾数的位数是有限的,这意味着浮点数只能精确地表示一定数量的小数位数。
二、精度丢失的原因
有限位数:由于浮点数的尾数位数有限,因此无法精确表示所有的十进制小数。当小数位数超过尾数的表示范围时,就会发生精度丢失。
舍入误差:在浮点数运算过程中,由于数值的内部表示不精确,运算结果也需要进行舍入处理以适应浮点数的存储格式。这种舍入误差会随着多次运算的累积而逐渐增大,最终导致精度丢失。
二进制与十进制的不匹配:由于二进制和十进制之间的不匹配,某些十进制小数在二进制中无法精确表示,这也会导致精度丢失。
三、精度丢失的影响
计算误差:精度丢失会导致计算结果与期望结果之间存在误差。这种误差在多次运算后会逐渐累积,最终影响结果的准确性。
比较问题:由于浮点数的精度问题,直接比较两个浮点数是否相等通常是不可靠的。即使两个浮点数的值在视觉上非常接近,它们在底层的二进制表示中也可能存在微小差异。
四、应对措施
使用BigDecimal类:在需要高精度计算的场景中,可以使用Java中的BigDecimal类来代替浮点数进行运算。BigDecimal类可以精确表示小数,并且允许开发者控制舍入模式,从而避免浮点数的精度问题。
引入误差容忍度:在比较两个浮点数时,可以引入误差容忍度(也称为epsilon),即允许两个浮点数的差值在某个很小的范围内视为相等。这样可以避免直接比较浮点数时产生的误差。
选择合适的数值类型:根据实际需求选择合适的数值类型,如float、double或BigDecimal。在可能的情况下,优先选择精度更高的数值类型以减少精度丢失的风险。
综上所述,浮点数运算时会有精度丢失的风险,这主要源于浮点数的表示方式和运算特性。为了降低这种风险,可以采取相应的应对措施来确保计算的准确性。
如何解决浮点数运算的精度丢失问题?
浮点数运算的精度丢失问题在计算机科学中是一个普遍存在的挑战,源于二进制无法精确表示某些十进制小数以及运算过程中的舍入误差。以下是一些解决浮点数运算精度丢失问题的方法:
一、使用整数进行计算
- 原理:
- 将浮点数转换为整数进行计算,可以避免浮点数表示不精确的问题。
- 通过放大或缩小数值的倍数(如乘以10的幂),将浮点数转换为整数进行计算,然后再将结果转换回浮点数。
function multiply(a, b) { const multiplier = 10000; // 选择一个合适的倍数,如10000 const intA = a * multiplier; const intB = b * multiplier; return (intA * intB) / (multiplier * multiplier);
}二、使用toFixed()方法
- 原理:
toFixed()方法可以将浮点数四舍五入到指定的小数位数。- 需要注意的是,
toFixed()返回的是一个字符串,需要使用parseFloat()将其转换回数字。
const result = parseFloat((0.1 + 0.2).toFixed(10));三、使用第三方库
- 原理:
- 有一些第三方库专门用于处理浮点数计算精度问题,如
decimal.js、bignumber.js等。 - 这些库提供了一系列方法来进行高精度的浮点数计算。
- 有一些第三方库专门用于处理浮点数计算精度问题,如
- 示例:
- 使用
decimal.js库:
- 使用
import Decimal from 'decimal.js';
const a = new Decimal(0.1);
const b = new Decimal(0.2);
const result = a.plus(b).toNumber();四、使用BigDecimal类(Java)
- 原理:
- 在Java中,
BigDecimal类可以精确表示小数,并且允许开发者控制舍入模式。 BigDecimal提供了丰富的数学运算方法,可以避免浮点数的精度问题。
- 在Java中,
import java.math.BigDecimal;
public class BigDecimalExample { public static void main(String[] args) { BigDecimal a = new BigDecimal("0.1"); BigDecimal b = new BigDecimal("0.2"); BigDecimal sum = a.add(b); System.out.println(sum); // 输出: 0.3 }
}五、引入误差容忍度(epsilon)
- 原理:
- 在比较两个浮点数时,由于它们在底层的二进制表示中可能存在微小差异,直接比较可能会导致错误的结果。
- 引入误差容忍度(epsilon),即允许两个浮点数的差值在某个很小的范围内视为相等。
double a = 0.1 + 0.2;
double b = 0.3;
double epsilon = 1e-10; // 容忍度
System.out.println(Math.abs(a - b) < epsilon); // 输出: true六、使用整数表示货币值
- 原理:
- 在处理货币运算时,可以使用整数来表示货币值(如以分为单位表示货币值而不是以元),从而避免浮点数精度问题。
int priceInCents = 100; // 1.00元表示为100分
int quantity = 3;
int totalCostInCents = priceInCents * quantity;
System.out.println("总价:" + (totalCostInCents / 100.0) + " 元"); // 输出: 3.00 元综上所述,解决浮点数运算精度丢失问题的方法有多种,可以根据具体场景和需求选择合适的方法。在实际应用中,应尽量避免在需要高精度计算的场景中使用浮点数,而是采用整数或其他高精度数据类型进行计算。
超过Long整型的数据应该如何表示?
基本数值类型都有一个表达范围,如果超过这个范围就会有数值溢出的风险。
在 Java 中,64 位 long 整型是最大的整数类型。
long l = Long.MAX_VALUE;
System.out.println(l + 1); // -9223372036854775808
System.out.println(l + 1 == Long.MIN_VALUE); // trueBigInteger 内部使用 int[] 数组来存储任意大小的整形数据。
相对于常规整数类型的运算来说,BigInteger 运算的效率会相对较低。
相关文章:
)
Java基础概览和常用知识(七)
什么是自动装箱和自动拆箱,原理是什么? 自动装箱和自动拆箱是Java编程语言中的两个重要概念,它们涉及到基本数据类型与其对应包装类之间的自动转换。 一、定义 自动装箱:是指Java编译器在需要将基本数据类型转换为对应的包装类…...

STL-string
STL的六大组件: string // string constructor #include <iostream> #include <string> using namespace std; int main() {// 构造std::string s0("Initial string");std::string s1; //nullptrstd::string s2("A character sequenc…...

数据库基础-学习版
目录 数据库巡检清理表空间高水位处理重建索引扩展字段异常恢复处置常见命令汇总 数据库巡检 数据库巡检的主要目的是确保数据库的健康状态、性能和安全,及时发现潜在的问题。 一 数据库状态检查 查看数据库列表:SHOW DATABASES; 检查当前数据库SELECT DATABASE(); 检查数据…...

【Gin】Gin框架介绍和使用
一、简单使用Gin框架搭建一个服务器 package mainimport ("github.com/gin-gonic/gin" )func main() {// 创建一个默认的路由引擎r : gin.Default()// GET 请求方法r.GET("/hello", func(c *gin.Context) {// c.JSON 返回的是JSON格式的数据c.JSON(200, g…...

AI大模型带来哪些创业机遇?
AI 大模型的快速发展带来了许多创新和创业机遇,涵盖了从行业应用到基础设施优化的方方面面。以下是一些具体的创业机会: 1、垂直行业应用 大模型可以根据不同行业的需求进行定制和优化,提供高度专业化的 AI 解决方案。 医疗领域:…...

[Linux] 层层深入理解文件系统——(3)磁盘组织存储的文件
标题:[Linux] 层层深入理解文件系统——(3)磁盘组织组织存储的文件 个人主页水墨不写bug 目录 一、磁盘中的文件 1)磁盘的物理结构 2)磁盘的CHS寻址法 3)磁盘的空间管理 二、磁盘如何组织存储文件 三…...

Apache Cordova学习计划
Apache Cordova(之前称为 PhoneGap): 1. PhoneGap的起源:2008年8月,PhoneGap在旧金山的iPhoneDevCamp上首次亮相,由Nitobe公司开发,目的是“为跨越Web技术和iPhone之间的鸿沟牵线搭桥”。 2. Ph…...

Unity学习日志-API
Untiy基本API 角度旋转自转相对于某一个轴 转多少度相对于某一个点转练习 角度 this.transform.rotation(四元数)界面上的xyz(相对于世界坐标) this.transform.eulerAngles;相对于父对象 this.transform.localEulerAngles;设置角度和设置位置一样,不能单独设置xz…...

Java基础常见面试题总结(上)
基础概念与常识 Java 语言有哪些特点? 简单易学(语法简单,上手容易);面向对象(封装,继承,多态);平台无关性( Java 虚拟机实现平台无关性)&…...

4 -《本地部署开源大模型》在Ubuntu 22.04系统下部署运行ChatGLM3-6B模型
在Ubuntu 22.04系统下部署运行ChatGLM3-6B模型 大模型部署整体来看并不复杂,且官方一般都会提供标准的模型部署流程,但很多人在部署过程中会遇到各种各样的问题,很难成功部署,主要是因为这个过程会涉及非常多依赖库的安装和更新及…...
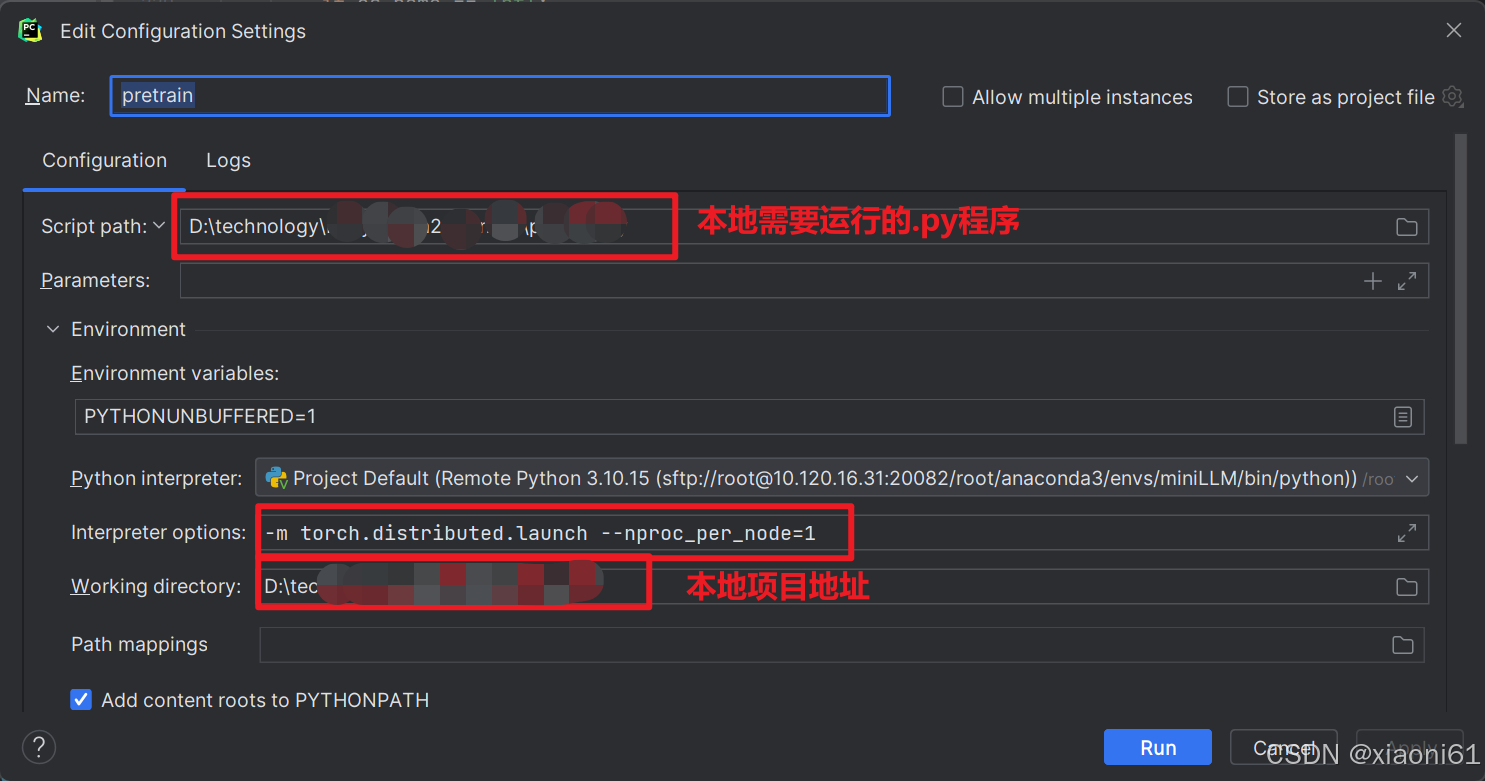
本地如何使用Pycharm连接远程服务器调试torchrun
pycharm 远程连接服务器并且debug, 支持torch.distributed.launch debug_pycharm远程debug-CSDN博客 上面这个博客写的真的非常好,记录一下,需要注意该博主的主机为mac 本人可调试版本为: 可直接运行版本为:...

Visual Studio 2022常用快捷键
1. 基本编辑快捷键 Ctrl X:剪切选中内容Ctrl C:复制选中内容Ctrl V:粘贴内容Ctrl Z:撤销Ctrl Y:重做Ctrl Shift L:删除当前行Ctrl K, Ctrl C:注释选中的代码Ctrl K, Ctrl U…...
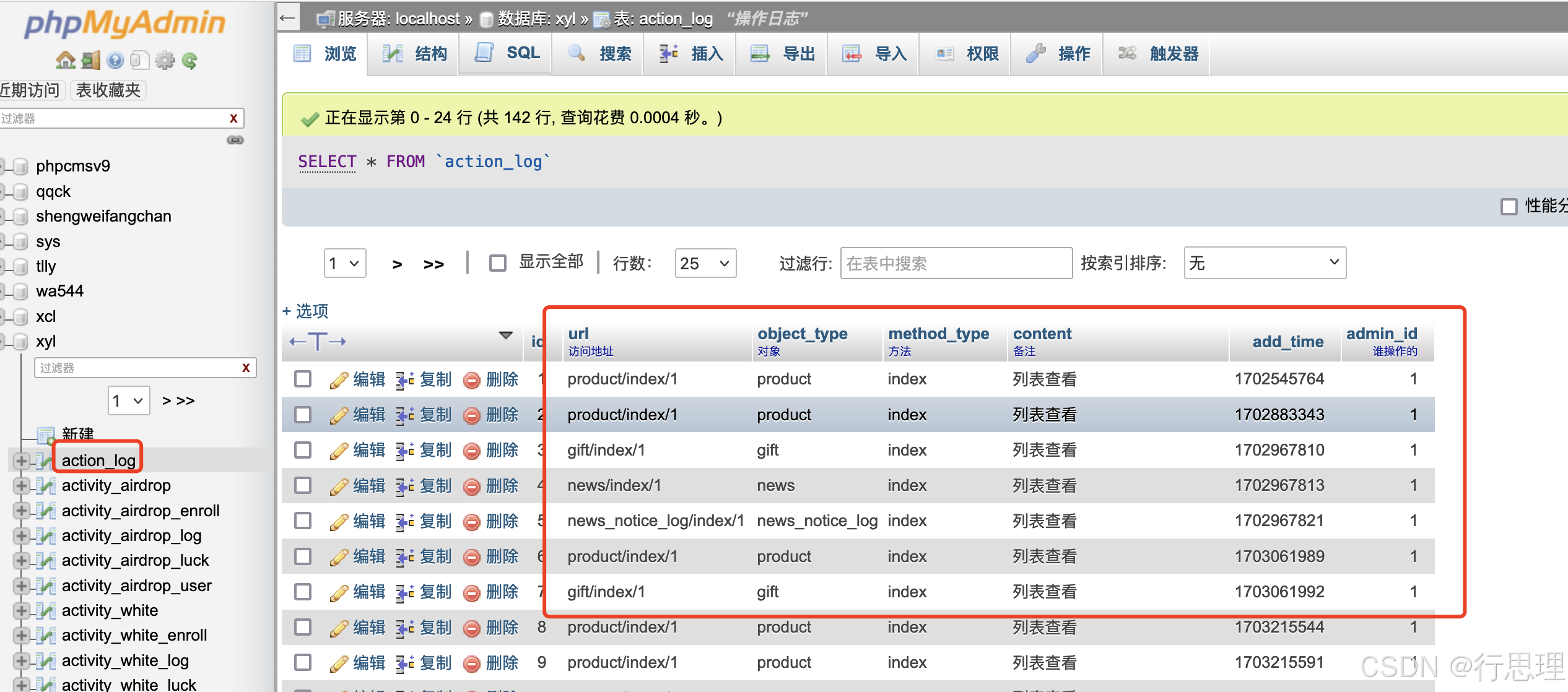
mysql innodb 引擎如何直接复制数据库文件?
mysql innodb 引擎如何直接复制数据库文件?介绍如下: 1、首先找到数据库文件所在位置 一般可以看my.conf/my.ini配置的文件的“datadir” 看示例: “MAMP”在Macos下的数据库文件位置: /Library/Application Support/appsolu…...

python中的global和nonlocal关键字以及闭包和模块
global i 这样的用法在于 Python 中,但需要在一个函数内部使用,以便将变量 i 声明为全局变量。让我们来详细讲解一下它的用法。 什么是全局变量? 全局变量是指在函数外部定义的变量,可以在任何函数中访问和修改。如果你需要在函数…...
LabVIEW风机滚动轴承监测系统
矿井主通风机作为矿井中最重要的通风设备,一旦出现故障,不仅会影响矿井内的空气质量,还可能引发安全事故。研究表明,通风机中约30%的故障是由轴承问题引起的。因此,能够实时监控矿井主通风机轴承状态的系统,…...

第1节 什么是鸿蒙系统
鸿蒙系统(HarmonyOS)是华为公司发布的一款基于微内核的面向全场景的分布式操作系统。以下是对它的具体介绍: 1. 核心特点: • 分布式能力:这是鸿蒙系统的核心优势之一。它能够将多种不同类型的智能终端设备连接起来&a…...

CentOS 7 将 YUM 源更改为国内镜像源
在 CentOS 7 中,将 YUM 源更改为国内的阿里云镜像源可以提高软件包的下载速度。以下是具体的步骤: 1. 备份原有 YUM 源配置 首先,建议你备份当前的 YUM 源配置,以防后续需要恢复: sudo cp -r /etc/yum.repos.d /etc…...

python调用dircmp进行文件夹比较
不同电脑上的同一部署文件,由于更新频率不相同导致两边内容有差异,需要比较两边的文件夹及文件差异。之前写过批量修改文件名的Python代码,因此优先想用python处理。 百度“python 文件夹对比”,不少文章都是自己实现的文件夹…...

微信小程序 - 供应链系统设计
文章目录 一、系统概述二、系统架构设计三、系统安全设计四、系统性能优化五、系统部署与维护 在当今数字化时代,供应链管理对于企业的高效运营至关重要。微信小程序作为一种便捷的移动应用形式,为供应链系统的开发提供了新的机遇。本文将从系统架构设计…...
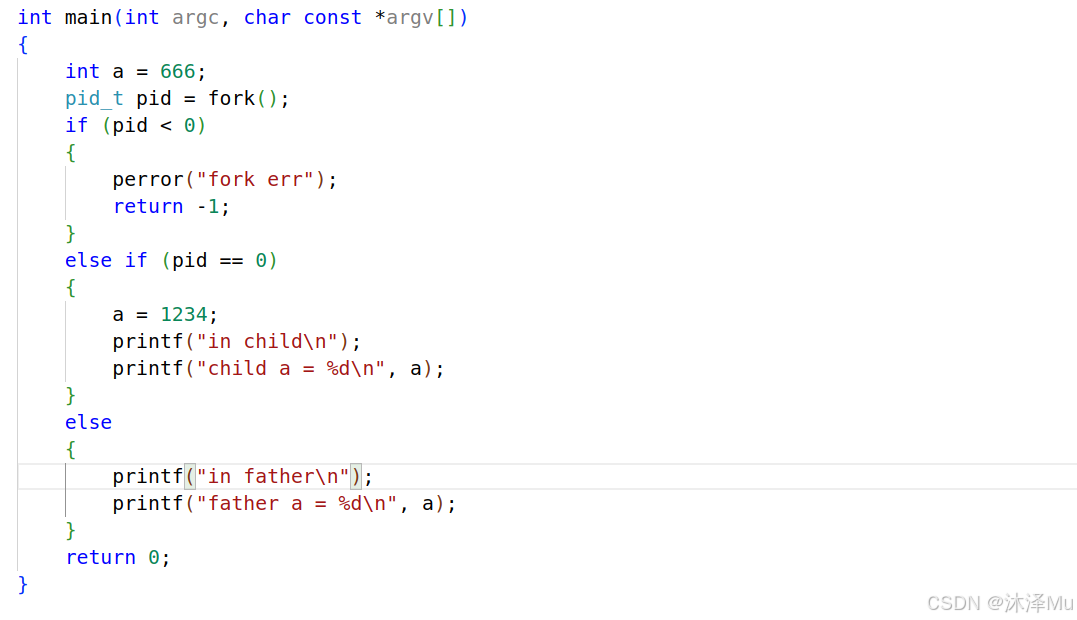
嵌入式学习-IO进程-Day03
嵌入式学习-IO进程-Day03 IO进程 获取文件属性(stat) 库 库的概念 库的分类 静态库的制作 动态库的制作 进程 进程和程序的区别 进程的特点 进程三段 进程的类型 进程的运行状态 进程状态转换图(重点) 进程的函数接口 创建进程for…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
