C++从入门到起飞之——红黑树 全方位剖析!

🌈个人主页:秋风起,再归来~
🔥系列专栏:C++从入门到起飞
🔖克心守己,律己则安
目录
1. 红⿊树的概念
2. 红⿊树的实现
2.1 构建整体框架
2.2 红黑树的插入
2.3 红黑树的验证
2.4 红黑树的其他简单接口
3、红黑树完整源码
4、完结散花
1. 红⿊树的概念
红⿊树是⼀棵⼆叉搜索树,他的每个结点增加⼀个存储位来表⽰结点的颜⾊,可以是红⾊或者⿊⾊。 通过对任何⼀条从根到叶⼦的路径上各个结点的颜⾊进⾏约束,红⿊树确保没有⼀条路径会⽐其他路 径⻓出2倍,因⽽是接近平衡的。
>红⿊树的规则:
1. 每个结点不是红⾊就是⿊⾊
2. 根结点是⿊⾊的
3. 如果⼀个结点是红⾊的,则它的两个孩⼦结点必须是⿊⾊的,也就是说任意⼀条路径不会有连续的 红⾊结点。
4. 对于任意⼀个结点,从该结点到其所有NULL结点的简单路径上,均包含相同数量的⿊⾊结点
说明:《算法导论》等书籍上补充了⼀条每个叶⼦结点(NIL)都是⿊⾊的规则。他这⾥所指的叶⼦结点 不是传统的意义上的叶⼦结点,⽽是我们说的空结点,有些书籍上也把NIL叫做外部结点。NIL是为了 ⽅便准确的标识出所有路径,《算法导论》在后续讲解实现的细节中也忽略了NIL结点,所以我们知道 ⼀下这个概念即可。

2. 红⿊树的实现
2.1 构建整体框架
枚举类型定义红黑色:
//枚举类型定义颜色
enum Colour
{RED,BLACK
};红黑树每个节点的结构:
//节点结构(默认存储pair类型的key/val结构)
template<class K, class V>
struct RBTreeNode
{RBTreeNode(const pair<K, V>& kv):_kv(kv), _parent(nullptr), _left(nullptr), _right(nullptr),_col(RED){}pair<K, V> _kv;RBTreeNode* _parent;RBTreeNode* _left;RBTreeNode* _right;Colour _col;//初始化为红色
};红黑树整体结构
//红黑树
template<class K,class V>
class RBTree
{typedef RBTreeNode Node;
public://各种接口的实现private:Node* _root=nullptr;
};2.2 红黑树的插入
1、红黑树是特殊的二叉搜索数,所以我们进行插入时,还是先按照二叉搜索数的规则进行插入!
//如果树为空,在根插入并且颜色为黑色
if (_root == nullptr)
{_root = new Node(kv);_root->_col = BLACK;return true;
}
//树不为空按搜索树规则先进行插入
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{if (kv.first < cur->_kv.first)//小往左走{parent = cur;cur = parent->_left;}else if (kv.first > cur->_kv.first)//大往右走{parent = cur;cur = parent->_right;}else{return false;//不支持相同元素的插入}
}
cur = new Node(kv);
cur->_col = RED;
if (kv.first < parent->_kv.first)//K小插入在左边parent->_left = cur;
else//K大插入在右边parent->_right = cur;
cur->_parent = parent;2、插入成功后,我们就要维护红黑树的规则了。
>如果插入节点的父亲是黑色,那插入后依然符合红黑树的规则,我们不用处理。
>如果插入节点的父亲是红色,那么此时就有连续的红色节点,我们就要进行处理。
a、插入节点的叔叔存在且为红,我们只需要进行变色。

变色原理:因为parent的颜色为红,所以g的颜色一定为黑。插入前从g开始的路径的黑色节点的数量相同,要解决连续红色节点的问题,我们必然要把parent变黑色。但从g到cur路径的黑色节点多了一个,所以我们把g变红,在把u变黑就完美的解决了问题!

不过,g变红后,又可能会引起祖先节点的连续红色节点问题,所以我们还要继续向上维护红黑树的规则!
变色代码实现
//插入后进行维护红黑树规则的逻辑
//parent存在且为红
while (parent&& parent->_col = RED)
{Node* grandfather = parent->_parent;//p在g的右边if (parent == grandfather->_right){//g//u pNode* uncle = grandfather->_left;if (uncle&& uncle->_col = RED)//uncle存在且为红{//变色处理uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//更新cur继续向上处理cur = grandfather;parent = cur->_parent;}else//uncle不存在或者存在且为黑{}}else//p在g的左边{//g//p uNode* uncle = grandfather->_left;if (uncle&& uncle->_col = RED)//uncle存在且为红{//变色处理uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//更新cur继续向上处理cur = grandfather;parent = cur->_parent;}else//uncle不存在或者存在且为黑{}}
}b、如果uncle不存在或者uncle存在且为黑,这时我们就要进行旋转加变色处理。
单旋+变色:
>如果uncle不存在,说明c一定是新增节点,如果c是变色后的节点,那么它在变色前一定是黑色,而从g开始的路径到c就多一个黑色节点!

>如果uncle存在且为黑,说明c一定是变色后的节点,如果c是新增的节点,那么从g开始的路径到u就多一个黑色节点!

变色原理:我们根据c、p、g的位置来选择合理的旋转逻辑,然后再把p变黑,g变红即可解决问题!
双旋+变色:
c为红,p为红,g为⿊,u不存在或者u存在且为⿊,u不存在,则c⼀定是新增结点,u存在且为⿊,则 c⼀定不是新增,c之前是⿊⾊的,是在c的⼦树中插⼊,符合情况1,变⾊将c从⿊⾊变成红⾊,更新上 来的。
分析:p必须变⿊,才能解决,连续红⾊结点的问题,u不存在或者是⿊⾊的,这⾥单纯的变⾊⽆法解 决问题,需要旋转+变⾊。

如果p是g的左,c是p的右,那么先以p为旋转点进⾏左单旋,再以g为旋转点进⾏右单旋,再把c变 ⿊,g变红即可。c变成课这颗树新的根,这样⼦树⿊⾊结点的数量不变,没有连续的红⾊结点了,且 不需要往上更新,因为c的⽗亲是⿊⾊还是红⾊或者空都不违反规则。

如果p是g的右,c是p的左,那么先以p为旋转点进⾏右单旋,再以g为旋转点进⾏左单旋,再把c变 ⿊,g变红即可。c变成课这颗树新的根,这样⼦树⿊⾊结点的数量不变,没有连续的红⾊结点了,且 不需要往上更新,因为c的⽗亲是⿊⾊还是红⾊或者空都不违反规则。

 插入完整代码:
插入完整代码:
bool insert(const pair<K, V>& kv)
{//如果树为空,在根插入并且颜色为黑色if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//树不为空按搜索树规则先进行插入Node* parent = nullptr;Node* cur = _root;while (cur){if (kv.first < cur->_kv.first)//小往左走{parent = cur;cur = parent->_left;}else if (kv.first > cur->_kv.first)//大往右走{parent = cur;cur = parent->_right;}else{return false;//不支持相同元素的插入}}cur = new Node(kv);cur->_col = RED;if (kv.first < parent->_kv.first)//K小插入在左边parent->_left = cur;else//K大插入在右边parent->_right = cur;cur->_parent = parent;//插入后进行维护红黑树规则的逻辑//parent存在且为红while (parent&& parent->_col == RED){Node* grandfather = parent->_parent;//p在g的右边if (parent == grandfather->_right){//g//u pNode* uncle = grandfather->_left;if (uncle&& uncle->_col == RED)//uncle存在且为红{//变色处理uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//更新cur继续向上处理cur = grandfather;parent = cur->_parent;}else//uncle不存在或者存在且为黑{if (cur == parent->_right){//g//u p// c//以g为旋转点进行左单旋RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//g//u p// c//进行右左双旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}//旋转+变色后链接祖先节点的节点为黑,必然不会发生连续红色节点的情况直接break;break;}}else//p在g的左边{//g//p uNode* uncle = grandfather->_left;if (uncle&& uncle->_col == RED)//uncle存在且为红{//变色处理uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//更新cur继续向上处理cur = grandfather;parent = cur->_parent;}else//uncle不存在或者存在且为黑{if (cur == parent->_left){//g//p u//c//以g为旋转点进行右单旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//g//p u// c//进行左右双旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}//旋转+变色后链接祖先节点的节点为黑,必然不会发生连续红色节点的情况直接break;break;}}}//如果持续更新变色到根_root->_col = BLACK;return true;
}2.3 红黑树的验证
>检查每条路径的黑色节点是否相等,是否有连续的红色节点
//检查每条路径的黑色节点是否相等,是否有连续的红色节点
bool Check(Node* root, int blackNum, const int refNum)
{if (root == nullptr){// 前序遍历⾛到空时,意味着⼀条路径⾛完了 //cout << blackNum << endl;if (refNum != blackNum){cout << "存在黑色结点的数量不相等的路径" << endl;return false;}return true;}// 检查孩⼦不太⽅便,因为孩⼦有两个,且不⼀定存在,反过来检查⽗亲就⽅便多了 if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红色节点" << endl;return false;}if (root->_col == BLACK){blackNum++;}return Check(root->_left, blackNum, refNum)&& Check(root->_right, blackNum, refNum);
}>检查平衡
//检查平衡
bool IsBalance()
{if (_root == nullptr)return true;if (_root->_col == RED)return false;// 参考值 int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);
}>插入一万个随机数看看是否平衡
void testInert()
{const int N = 10000;RBTree<int, int> t;vector<int> v;srand((unsigned int)time(nullptr));for (int i = 0; i < N; i++){v.push_back(rand() + i);}for (auto e : v){t.insert({ e,e });}cout << t.IsBalance() << endl;
}
2.4 红黑树的其他简单接口
//默认构造
RBTree() = default;
//拷贝构造
RBTree(const RBTree<K,V>& rbt)
{_root=_copy(rbt._root);
}
// 赋值重载
RBTree<K, V>& operator=(RBTree<K, V> tmp)
{std::swap(_root, tmp._root);return *this;
}
//中序遍历
void InOrder()
{_InOrder(_root);
}
//二叉树的析构
~RBTree()
{_Destroy(_root);
}private:
//递归拷贝
Node* _copy(Node* root)
{if (root == nullptr)return nullptr;Node* newNode = new Node(root->_kv);newNode->_left = _copy(root->_left);newNode->_right = _copy(root->_right);return newNode;
}
//中序遍历
void _InOrder(Node* root)
{if (root == nullptr)return;_InOrder(root->_left);cout << "<" << root->_kv.first << "," << root->_kv.second << ">" << endl;_InOrder(root->_right);
}
//二叉树的销毁
void _Destroy(Node* root)
{if (root == nullptr)return;_Destroy(root->_left);_Destroy(root->_right);delete root;
}3、红黑树完整源码


#pragma once
#include<iostream>
using namespace std;
//枚举类型定义颜色
enum Colour
{RED,BLACK
};
//节点结构(默认存储pair类型的key/val结构)
template<class K, class V>
struct RBTreeNode
{RBTreeNode(const pair<K, V>& kv):_kv(kv), _parent(nullptr), _left(nullptr), _right(nullptr),_col(RED){}pair<K, V> _kv;RBTreeNode* _parent;RBTreeNode* _left;RBTreeNode* _right;Colour _col;//初始化为红色
};//红黑树
template<class K,class V>
class RBTree
{typedef RBTreeNode<K,V> Node;
public://默认构造RBTree() = default;//拷贝构造RBTree(const RBTree<K,V>& rbt){_root=_copy(rbt._root);}// 赋值重载RBTree<K, V>& operator=(RBTree<K, V> tmp){std::swap(_root, tmp._root);return *this;}//中序遍历void InOrder(){_InOrder(_root);}//二叉树的析构~RBTree(){_Destroy(_root);}//红黑树的查找Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}//红黑树的插入bool insert(const pair<K, V>& kv){//如果树为空,在根插入并且颜色为黑色if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}//树不为空按搜索树规则先进行插入Node* parent = nullptr;Node* cur = _root;while (cur){if (kv.first < cur->_kv.first)//小往左走{parent = cur;cur = parent->_left;}else if (kv.first > cur->_kv.first)//大往右走{parent = cur;cur = parent->_right;}else{return false;//不支持相同元素的插入}}cur = new Node(kv);cur->_col = RED;if (kv.first < parent->_kv.first)//K小插入在左边parent->_left = cur;else//K大插入在右边parent->_right = cur;cur->_parent = parent;//插入后进行维护红黑树规则的逻辑//parent存在且为红while (parent&& parent->_col == RED){Node* grandfather = parent->_parent;//p在g的右边if (parent == grandfather->_right){//g//u pNode* uncle = grandfather->_left;if (uncle&& uncle->_col == RED)//uncle存在且为红{//变色处理uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//更新cur继续向上处理cur = grandfather;parent = cur->_parent;}else//uncle不存在或者存在且为黑{if (cur == parent->_right){//g//u p// c//以g为旋转点进行左单旋RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//g//u p// c//进行右左双旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}//旋转+变色后链接祖先节点的节点为黑,必然不会发生连续红色节点的情况直接break;break;}}else//p在g的左边{//g//p uNode* uncle = grandfather->_right;if (uncle&& uncle->_col == RED)//uncle存在且为红{//变色处理uncle->_col = parent->_col = BLACK;grandfather->_col = RED;//更新cur继续向上处理cur = grandfather;parent = cur->_parent;}else//uncle不存在或者存在且为黑{if (cur == parent->_left){//g//p u//c//以g为旋转点进行右单旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//g//p u// c//进行左右双旋RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}//旋转+变色后链接祖先节点的节点为黑,必然不会发生连续红色节点的情况直接break;break;}}}//如果持续更新变色到根_root->_col = BLACK;return true;}//检查平衡bool IsBalance(){if (_root == nullptr)return true;if (_root->_col == RED)return false;// 参考值 int refNum = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK){++refNum;}cur = cur->_left;}return Check(_root, 0, refNum);}private://右单旋void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;Node* pParent = parent->_parent;parent->_left = subLR;if (subLR)//如果不为空subLR->_parent = parent;subL->_right = parent;parent->_parent = subL;if (pParent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (pParent->_left == parent){pParent->_left = subL;}else{pParent->_right = subL;}subL->_parent = pParent;}}//左单旋void RotateL(Node* parent){Node* pParent = parent->_parent;Node* subR = parent->_right;Node* subRL = subR->_left;subR->_left = parent;parent->_parent = subR;parent->_right = subRL;if (subRL)subRL->_parent = parent;if (pParent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (pParent->_left == parent){pParent->_left = subR;}else{pParent->_right = subR;}subR->_parent = pParent;}}//检查每条路径的黑色节点是否相等,是否有连续的红色节点bool Check(Node* root, int blackNum, const int refNum){if (root == nullptr){// 前序遍历⾛到空时,意味着⼀条路径⾛完了 //cout << blackNum << endl;if (refNum != blackNum){cout << "存在黑色结点的数量不相等的路径" << endl;return false;}return true;}// 检查孩⼦不太⽅便,因为孩⼦有两个,且不⼀定存在,反过来检查⽗亲就⽅便多了 if (root->_col == RED && root->_parent->_col == RED){cout << root->_kv.first << "存在连续的红色节点" << endl;return false;}if (root->_col == BLACK){blackNum++;}return Check(root->_left, blackNum, refNum)&& Check(root->_right, blackNum, refNum);}//递归拷贝Node* _copy(Node* root){if (root == nullptr)return nullptr;Node* newNode = new Node(root->_kv);newNode->_left = _copy(root->_left);newNode->_right = _copy(root->_right);return newNode;}//中序遍历void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << "<" << root->_kv.first << "," << root->_kv.second << ">" << endl;_InOrder(root->_right);}//二叉树的销毁void _Destroy(Node* root){if (root == nullptr)return;_Destroy(root->_left);_Destroy(root->_right);delete root;}private:Node* _root=nullptr;
};4、完结散花
好了,这期的分享到这里就结束了~
如果这篇博客对你有帮助的话,可以用你们的小手指点一个免费的赞并收藏起来哟~
如果期待博主下期内容的话,可以点点关注,避免找不到我了呢~
我们下期不见不散~~


相关文章:

C++从入门到起飞之——红黑树 全方位剖析!
🌈个人主页:秋风起,再归来~🔥系列专栏:C从入门到起飞 🔖克心守己,律己则安 目录 1. 红⿊树的概念 2. 红⿊树的实现 2.1 构建整体框架 2.2 红黑树的插入 2.3 红黑树的验证 2.4 红黑树…...
Java基于SSM微信小程序物流仓库管理系统设计与实现(lw+数据库+讲解等)
选题背景 随着社会的发展,社会的方方面面都在利用信息化时代的优势。互联网的优势和普及使得各种系统的开发成为必需。 本文以实际运用为开发背景,运用软件工程原理和开发方法,它主要是采用java语言技术和mysql数据库来完成对系统的设计。整个…...

[LeetCode] 733. 图像渲染
题目描述: 有一幅以 m x n 的二维整数数组表示的图画 image ,其中 image[i][j] 表示该图画的像素值大小。你也被给予三个整数 sr , sc 和 color 。你应该从像素 image[sr][sc] 开始对图像进行上色 填充 。 为了完成 上色工作: 从初始像素…...

智能EDA小白从0开始 —— DAY23 PyAether深度解析与技术展望
引言:技术革新与行业需求的碰撞 在半导体行业快速发展的今天,芯片设计的复杂性和对效率的要求日益提升。传统的芯片设计工具和方法已经难以满足当前行业的需求,特别是在面对大规模、高性能芯片的设计时,设计师们面临着前所未有的…...
从深海探测到海洋强国:数字孪生助力海洋装备跨越式发展
海洋广袤无垠,蕴藏着丰富的资源。近现代以来,人类使用各种手段探索海洋探索,广袤无垠的海洋与人类的生活越来越紧密,至少10亿人口摄入的蛋白质来自海洋,全球超过90%的货物、数据信息交流在海洋中转;海洋中丰…...
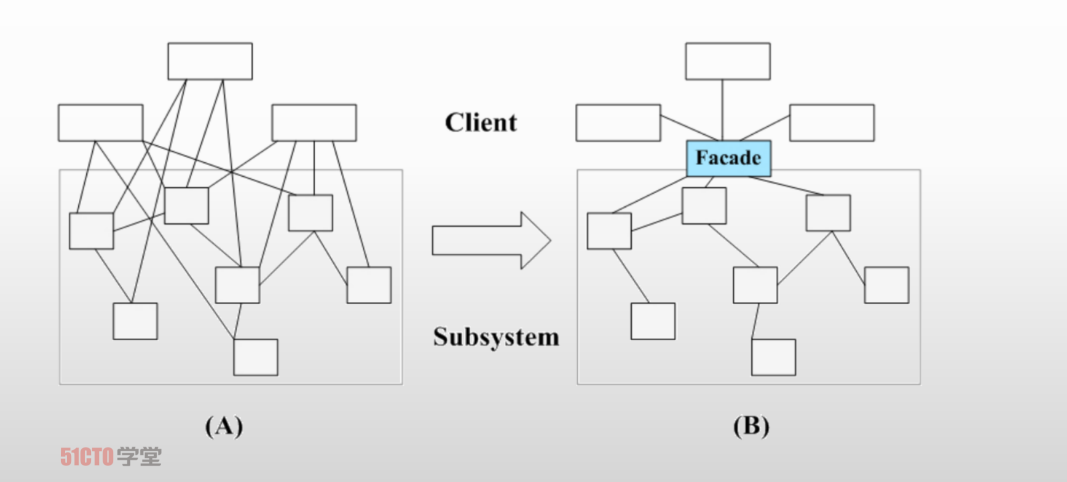
架构师备考-背诵精华(系统质量属性)
系统质量属性 根据GB/T 16260.1 定义,从管理角度对软件系统质量进行度量,可将影响软件质量的主要因素划分为6种维度特性包括:功能性、可靠性、易用性、效率、维护性、可移植性 功能性 适合性、准确性、互操作性、依从性、安全性 可靠性 容错…...

Pycharm下载安装教程(详细步骤)+汉化设置教程
今天讲解的是Pycharm安装教程和配置汉化设置,希望能够帮助到大家。 创作不易,还请各位同学三连点赞!!收藏!!转发!!! 对于刚入门学习Python还找不到方向的小伙伴可以试试…...

网络安全入门
网络安全入门是指学习和了解网络安全基础知识和技术的入门阶段。网络安全是指保护计算机系统、网络和数据免受未经授权的访问、使用、泄露、破坏以及其他威胁的技术和措施。 要入门网络安全,可以按照以下步骤进行: 了解网络安全基本概念:学习…...

你真的了解Canvas吗--解密十【ZRender篇】
目录 👊🏻入口 动画讲解二 Animator Element Transformable graphic 总结 书接上篇你真的了解Canvas吗--解密九【ZRender篇】由于一个bug的篇幅需要续写这个下篇,不过那块的bug内容对我们这篇要讲的动画也是息息相关的,因为Transformable这个类主要就是和变换相…...

mac安装brew时踩坑解决方案
安装包 mac上如果按照git等工具可能会使用brew,例如使用:$ brew install git命令,如果电脑没有按照brew,则会提示:zsh: command not found: brew 解决方案 需要我们打开brew的官网https://brew.sh/,复制…...
基于Handsontable.js + Excel.js实现表格预览和导出功能(公式渲染)
本文记录在html中基于Handsontable.js Excel.js实现表格预览、导出、带公式单元格渲染功能,在这里我们在html中实现,当然也可以在vue、react等框架中使用npm下载导入依赖文件。 Handsontable官方文档 一、开发前的准备引入相关依赖库 <!DOCTYPE ht…...
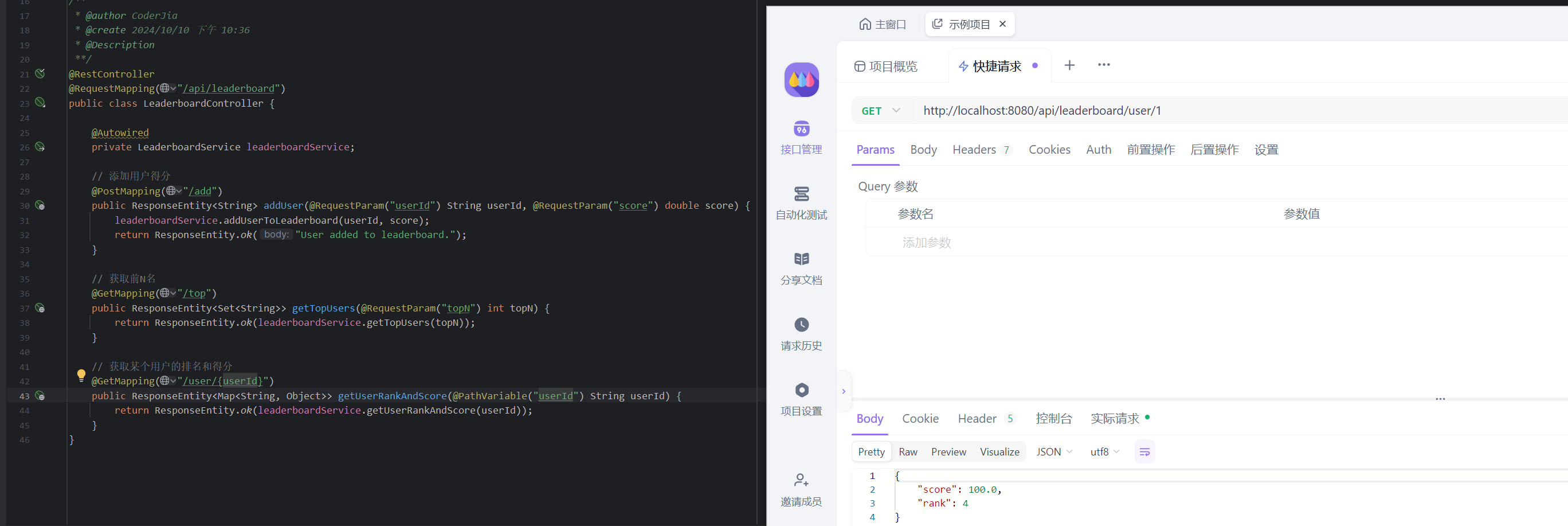
重学SpringBoot3-集成Redis(十三)之点排行榜实现
更多SpringBoot3内容请关注我的专栏:《SpringBoot3》 期待您的点赞👍收藏⭐评论✍ 重学SpringBoot3-集成Redis(十三)之点排行榜实现 1. 为什么选择 Redis 来实现排行榜?2. 项目环境准备2.1. 添加依赖2.2. 配置 Redis 连…...

Java 中方法参数传递的陷阱
前言 在编程过程中,我们经常会遇到一些看似简单却容易出错的问题。本文将通过一个具体的例子,探讨 Java 中方法参数传递的陷阱,并提供详细的解决方法。希望这篇文章能帮助你在未来的开发中避免类似的错误。 问题背景 假设我们的任务是计算…...

哪家云电脑便宜又好用?ToDesk云电脑、顺网云、达龙云全方位评测
陈老老老板🤴 🧙♂️本文专栏:生活(主要讲一下自己生活相关的内容)生活就像海洋,只有意志坚强的人,才能到达彼岸。 🧙♂️本文简述:讲一下市面上云电脑的对比。 🧙♂️上一篇文…...

【汇编语言】寄存器(内存访问)(三)—— 字的传送
文章目录 前言1. 字的传送2. 问题一3. 问题一的分析与解答4. 问题二5. 问题二的分析与解答结语 前言 📌 汇编语言是很多相关课程(如数据结构、操作系统、微机原理)的重要基础。但仅仅从课程的角度出发就太片面了,其实学习汇编语言…...

6 机器学习之应用现状
在过去二十年中,人类收集、存储、传输、处理数据的能力取得了飞速提升,人类社会的各个角落都积累了大量数据,亟需能有效地对数据进行分析利用的计算机算法,而机器学习恰顺应了大时代的这个迫切需求,因此该学科领域很自…...

相似度为 K 的字符串
题目链接 相似度为 K 的字符串 题目描述 注意 s1和s2只包含集合 {‘a’, ‘b’, ‘c’, ‘d’, ‘e’, ‘f’} 中的小写字母s2是s1的一个字母异位词 解答思路 可以深度优先遍历交换字母使得s1和s2尽可能接近,基本思路是:设定一个指针idx指向s1和s2的…...

[云] Project Analysis
项目要求分析: 开放性选题: 主题范围:任何与云计算系统相关的主题。项目类型:可以是技术、商业或研究项目。团队规模:最多可组成三人小组。 示例主题: 分析公共云数据:例如,AWS公共数…...

腾讯六宫格本地识别,本地模型识别,腾讯六图识别
基于K哥爬虫昨天发的文章,特此训练了一版腾讯模型,效果不错,特此感谢K哥的指导,效果如下图: 有需求,有疑问的欢迎评论区点出...
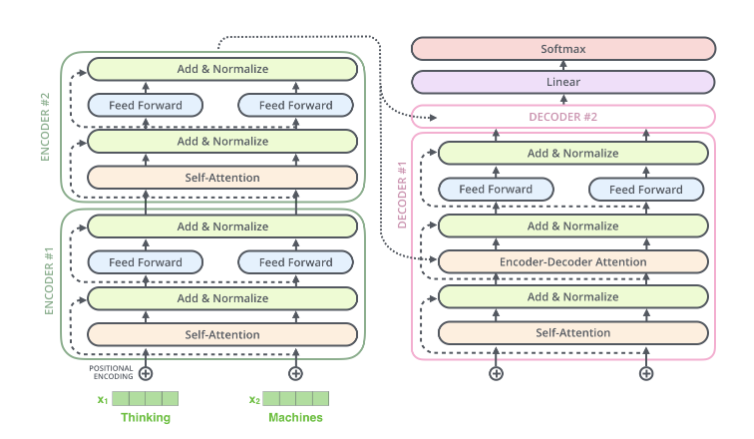
Transformer图解以及相关的概念
前言 transformer是目前NLP甚至是整个深度学习领域不能不提到的框架,同时大部分LLM也是使用其进行训练生成模型,所以transformer几乎是目前每一个机器人开发者或者人工智能开发者不能越过的一个框架。接下来本文将从顶层往下去一步步掀开transformer的面…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
