C++ | Leetcode C++题解之第493题翻转对
题目:

题解:
class BIT {
private:vector<int> tree;int n;public:BIT(int _n) : n(_n), tree(_n + 1) {}static constexpr int lowbit(int x) {return x & (-x);}void update(int x, int d) {while (x <= n) {tree[x] += d;x += lowbit(x);}}int query(int x) const {int ans = 0;while (x) {ans += tree[x];x -= lowbit(x);}return ans;}
};class Solution {
public:int reversePairs(vector<int>& nums) {set<long long> allNumbers;for (int x : nums) {allNumbers.insert(x);allNumbers.insert((long long)x * 2);}// 利用哈希表进行离散化unordered_map<long long, int> values;int idx = 0;for (long long x : allNumbers) {values[x] = ++idx;}int ret = 0;BIT bit(values.size());for (int i = 0; i < nums.size(); i++) {int left = values[(long long)nums[i] * 2], right = values.size();ret += bit.query(right) - bit.query(left);bit.update(values[nums[i]], 1);}return ret;}
};相关文章:

C++ | Leetcode C++题解之第493题翻转对
题目: 题解: class BIT { private:vector<int> tree;int n;public:BIT(int _n) : n(_n), tree(_n 1) {}static constexpr int lowbit(int x) {return x & (-x);}void update(int x, int d) {while (x < n) {tree[x] d;x lowbit(x);}}in…...

Git 修改分支名
在Git中修改分支名称,可以使用以下步骤: 切换到要重命名分支之外的其他分支: git checkout <其他分支名>重命名本地分支: git branch -m <旧分支名> <新分支名>如果需要删除远程的旧分支并创建新分支࿱…...

[自动化测试:Selenium]:环境部署和Webdriver的使用
文章目录 修改安装源打开Python Packages。点击梅花按钮。在弹出的对话框中,填入Name(随便填),Repository URL,选择下列的源,一般先选择清华源按OK确认。配置完成 安装seleniumFile→Settings→Project&…...

51单片机——OLED显示图片
取模软件:链接:https://pan.baidu.com/s/1UcrbS7nU4bsawNxsaaULfQ 提取码:gclc 1、如果图片大小和格式不合适,可以先用Img2Lcd软件进行调整图片大小,一般取模软件使用的是.bmp图片,可以进行输出.bmp格式。软件界面如下࿱…...

Gin 协程mysql客户端
一、Gin框架 mysql配置 这里选择yaml文件配置 二、配置读取 viper 读取yaml文件中对应配置 三、mysql 的协程客户端 文件位置 package databaseimport ("database/sql""fmt""github.com/spf13/viper""log""net/http"&quo…...

量子门电路开销——T门、clifford门、toffoli门、fredkin门
在量子计算中,T门的成本比Clifford门高出很多倍的原因与量子计算中纠错的实现、物理门操作的复杂性以及容错量子计算架构中的成本评估有关。以下是几个关键原因,解释了为什么 T 门的成本在量子计算中远远高于 Clifford 门: 1. T 门和 Cliffo…...
:类型转换关键字)
C++之《剑指offer》学习记录(1):类型转换关键字
笔者最近在找工作时,无意间读到了一本名为《剑指offer》的书,粗略翻阅了一下,感觉这将会是一本能让我不再苦恼于笔试和面试“手搓代码”的书。故笔者写下该系列博客记录自己的学习历程,希望能和这本书的读者朋友们一起交流学习心得…...

【Linux】平台设备驱动
在设备驱动模型中,引入总线的概念可以对驱动代码和设备信息进行分离。但是驱动中总线的概念是软件层面的一种抽象,与我们SOC中物理总线的概念并不严格相等。 物理总线:芯片与各个功能外设之间传送信息的公共通信干线,其中又包括数…...

【Linux】命令行参数环境变量
文章目录 命令行参数环境变量环境变量的概念常见环境变量查看环境变量测试PATH修改PATH HOME和环境变量相关的命令环境变量是如何被组织的通过系统调用putenv和getenv获取或设置环境变量环境变量通常是具有全局属性的普通变量与环境变量的区别 命令行参数 main函数有三种形式&…...

libaom 源码分析:twopass_encoder.c 文件
libaom libaom 是 AOMedia(开放媒体联盟)开发的一个开源视频编解码器库,它是 AV1 视频压缩格式的参考实现,并被广泛用于多种生产系统中。libaom 支持多种功能,包括可扩展视频编码(SVC)、实时通信…...

ruoyi同时支持mysql+sqlserver+oracle+postgresql
需求背景 最近需要一个小demo,项目中需要同时连接sqlserver和mysql数据库。 操作教程 1、pom.xml -- 修改common/pom.xml<!-- 动态数据源 --> <dependency><groupId>com.baomidou</groupId><artifactId>dynamic-datasource-spring-boot-star…...

微信小程序绘制轨迹
1、map | uni-app官网 根据官网描述:通过从数据库获取POI数据,并通过 uni-id-common 内的路线规划API,计算路线、距离、时间。 2、 <map style"width:100%;height:96%;" id"myMap" :scale"scale" :longi…...

UNION 联合查询
1.UNION ALL联合查询 同样为了演示方便,先向 teacher 表插入多条测试数据: INSERT INTO teacher (name,age,id_number,email) VALUES (姓名一,17,42011720200604077X,NULL), (姓名二,18,42011720200604099X,123qq.com), (姓名三,19,42011720200604020X…...

blender 理解 积木组合 动画制作 学习笔记
一、学习blender视频教程链接 案例2:积木组合_动画制作_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Bt4y1E7qn?vd_sourced0ea58f1127eed138a4ba5421c577eb1&p10&spm_id_from333.788.videopod.episodes 二、说明 之前已经学习了如何制作积木组…...

关于 FreeSWITCH mod_sofia 注册过期时间的测试
FreeSWITCH 版本:1.10.12,以下简称 Fs SIP 终端:Eyebeam 1.5.14.4 Eyebeam 设置注册的过期时间为 30 Fs 设置为 120,下面是详细配置: <param name"sip-force-expires-max" value"120"/>…...

【LeetCode:349. 两个数组的交集 + 哈希表】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
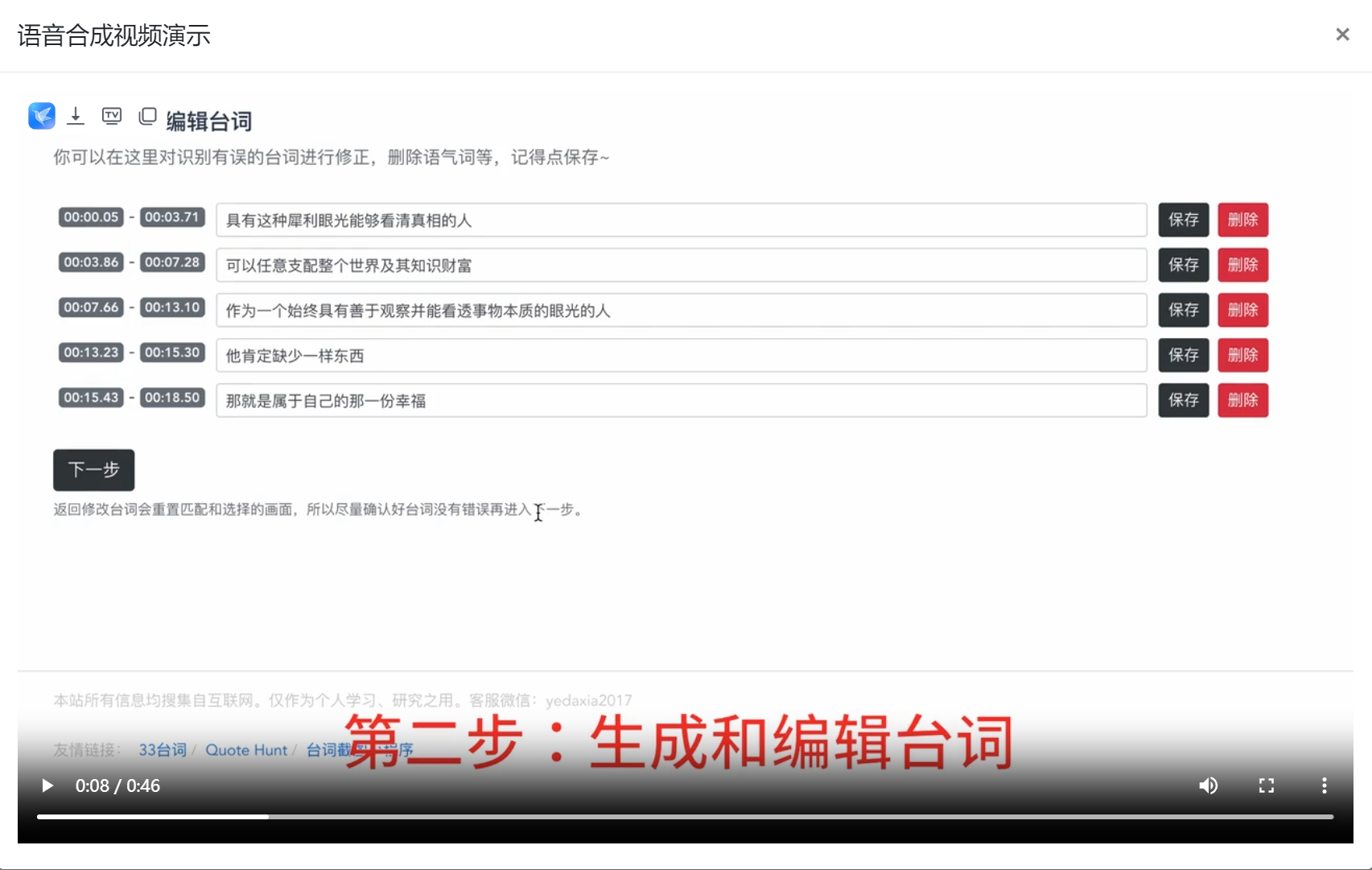
根据语音生成视频33搜帧
33搜帧,是一个能根据语音生成视频的网站,33搜帧 - 视频帧画面搜索引擎 33搜帧是一个使用AI技术构建的视频帧画面搜索引擎,和一般素材平台通过视频标签来搜索视频不同,33搜帧能搜索到视频素材中的每一帧画面,这个功能可…...

目标检测数据集图片及标签同步锐化
在目标检测任务中,数据集的质量直接影响到模型的性能。数据增强作为提升数据集多样性和模型泛化能力的常用手段,在图像处理过程中扮演着重要角色。锐化(Sharpening)技术是常见的图像增强方法之一,能够突出图像中的细节…...

滚雪球学Redis[6.4讲]:Redis消息队列:构建高效的消息通信与任务调度系统
全文目录: 🎉前言🚦Redis消息队列的使用场景🐳1. 异步任务处理🐋2. 任务调度🐬3. 模块解耦 ⚙️实现发布/订阅模型🐟️1. 发布者发布消息🐠2. 订阅者订阅频道🐡3. 实际应…...

《计算机视觉》—— 换脸
效果如下: 完整代码: import cv2 import dlib import numpy as npJAW_POINTS list(range(0, 17)) RIGHT_BROW_POINTS list(range(17, 22)) LEFT_BROW_POINTS list(range(22, 27)) NOSE_POINTS list(range(27, 35)) RIGHT_EYE_POINTS list(range(36…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
