支持向量机SVM原理详解
SVM原理详解
- 1、超平面
- 2、SVM原理
- 1. 问题定义
- 2. 分类决策
- 得到约束条件
- 3. 最大化间隔
- 4. 优化目标
- 3、凸优化问题
- 1. 原始优化问题
- 优化目标
- 约束条件
- 2. 拉格朗日乘子法
- 3. 拉格朗日函数分析
- 4. 求解对 w w w 和 b b b 的极值
- 5. 构造对偶问题
- 对偶问题的约束条件:
- 6、通过支持向量求解 b b b
- 支持向量的条件
- 7. 对偶问题的解法
- 4、非线性如何划分
- 1. 非线性数据问题
- 2. 核技巧的核心思想
- 3. 常见的核函数
- 1. 线性核(Linear Kernel)
- 2. 多项式核(Polynomial Kernel)
- 3. 高斯径向基核(RBF Kernel)/ 高斯核
- 4. Sigmoid 核(类似于神经网络的激活函数)
- 4. 使用核技巧的 SVM 优化问题
- 对偶优化目标:
- 约束条件:
- 5. SVM 的决策函数
- 6. 核函数的选择
- 5、软间隔
- 1、允许部分错误分类
- 软间隔 SVM 的目标函数和约束条件
- 目标函数:
- 约束条件:
- 6、正则化:控制模型的复杂度
- 7、软间隔和核函数结合
- 使用核函数的软间隔 SVM 优化目标
- 对偶优化问题
- 约束条件
1、超平面
在数学和几何中,超平面(Hyperplane)是一个通用化的几何概念。它是用来描述高维空间中的某个维度少一维的子空间。例如:
- 在二维空间(平面)中,超平面就是一条直线,它将平面分成两个部分。
- 在三维空间(我们通常理解的三维世界)中,超平面是一个平面,它将空间分成两个部分。
- 在更高的维度中,例如四维或更高维空间,超平面则是比空间维数低一维的几何对象,它同样将高维空间分成两个部分。
从数学表达上,超平面通常可以用一个线性方程来表示,如:
w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b = 0 w_1 x_1 + w_2 x_2 + \cdots + w_n x_n + b = 0 w1x1+w2x2+⋯+wnxn+b=0
其中 w 1 , w 2 , … , w n w_1, w_2, \dots, w_n w1,w2,…,wn 是权重, b b b 是偏差项,而 x 1 , x 2 , … , x n x_1, x_2, \dots, x_n x1,x2,…,xn 是 n 维空间中的坐标。这个方程的解就是超平面在该空间中的位置。
在机器学习(尤其是支持向量机)中,超平面用于将数据点分成不同的类别。
2、SVM原理
支持向量机(Support Vector Machine, SVM)是一种监督学习算法,广泛用于分类问题。它的核心思想是通过一个超平面来最大化不同类别之间的间隔,从而实现分类。下面我们从数学的角度来详细说明支持向量机的原理。
1. 问题定义
假设我们有一个线性可分的二分类问题,训练数据集表示为 ( { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) } ( \{(x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)\} ({(x1,y1),(x2,y2),…,(xn,yn)}),其中 ( x i ∈ R d ( x_i \in \mathbb{R}^d (xi∈Rd) 是特征向量, ( y i ∈ { − 1 , 1 } ( y_i \in \{-1, 1\} (yi∈{−1,1}) 是类标签。
SVM 的目标是找到一个超平面将不同类别的数据点分开,这个超平面的方程可以表示为:
w T x + b = 0 w^T x + b = 0 wTx+b=0
其中:
- ( w ( w (w) 是法向量,决定超平面的方向。
- ( b ( b (b) 是偏置项,决定超平面与原点的距离。
2. 分类决策
对于给定的样本点 ( x ),分类决策依据超平面的方程进行:
- 如果 ( w T x + b > 0 ( w^T x + b > 0 (wTx+b>0),则分类为 ( 1 ) 类。
- 如果 ( w T x + b < 0 ( w^T x + b < 0 (wTx+b<0),则分类为 ( -1 ) 类。
对于给定的训练样本 ( ( x i , y i ) ( (x_i, y_i) ((xi,yi)),其中 ( y i ∈ { 1 , − 1 } ( y_i \in \{1, -1\} (yi∈{1,−1}) 表示分类标签,支持向量机的目标是确保这些样本点能够被正确分类。
- 如果 ( y i = 1 ( y_i = 1 (yi=1)(正类),我们希望该点在超平面的正侧,即满足:
w T x i + b > 0 w^T x_i + b > 0 wTxi+b>0
- 如果 ( y i = − 1 ( y_i = -1 (yi=−1)(负类),我们希望该点在超平面的负侧,即满足:
w T x i + b < 0 w^T x_i + b < 0 wTxi+b<0
可以将这两个条件合并为一个不等式:
y i ( w T x i + b ) > 0 y_i (w^T x_i + b) > 0 yi(wTxi+b)>0
这个条件确保了所有样本点都被正确分类。对于 ( y i = 1 ( y_i = 1 (yi=1)的样本,如果 ( w T x i + b > 0 ( w^T x_i + b > 0 (wTxi+b>0),则 y i ( w T x i + b ) = 1 ⋅ ( w T x i + b ) > 0 y_i (w^T x_i + b) = 1 \cdot (w^T x_i + b) > 0 yi(wTxi+b)=1⋅(wTxi+b)>0;对于 ( y i = − 1 ( y_i = -1 (yi=−1) 的样本,如果 ( w T x i + b < 0 ( w^T x_i + b < 0 (wTxi+b<0),则 y i ( w T x i + b ) = − 1 ⋅ ( w T x i + b ) > 0 y_i (w^T x_i + b) = -1 \cdot (w^T x_i + b) > 0 yi(wTxi+b)=−1⋅(wTxi+b)>0。
得到约束条件
在支持向量之外的样本,应该位于超平面外更远的地方,因此我们可以将分类条件拓展为所有样本都必须至少满足 ( y i ( w T x i + b ) ≥ 1 ( y_i (w^T x_i + b) \geq 1 (yi(wTxi+b)≥1),即:
y i ( w T x i + b ) ≥ 1 ∀ i y_i (w^T x_i + b) \geq 1 \quad \forall i yi(wTxi+b)≥1∀i
这个条件表示所有样本点必须被正确分类,并且支持向量与超平面的距离为 1。
3. 最大化间隔
SVM 的关键在于找到能够最大化间隔(margin)的超平面。间隔指的是超平面到距离它最近的点的距离。
- 支持向量:离超平面最近的那些点称为支持向量。SVM 试图使得支持向量到超平面的距离最大化。
- 间隔的计算:对于一个点 ( x i ( x_i (xi),它到超平面的距离是:
Distance = ∣ w T x i + b ∣ ∥ w ∥ \text{Distance} = \frac{|w^T x_i + b|}{\|w\|} Distance=∥w∥∣wTxi+b∣
为了使得间隔最大化,支持向量机引入了支持向量的概念。支持向量是最靠近超平面的点,其几何上距离超平面的距离为 ( 1 ∥ w ∥ \frac{1}{\|w\|} ∥w∥1)。我们希望通过约束条件,将最靠近超平面的点(支持向量)的几何距离标准化为 1。
因此,对于支持向量,我们约定满足刚好分类正确的条件:
y i ( w T x i + b ) = 1 y_i (w^T x_i + b) = 1 yi(wTxi+b)=1
这意味着支持向量到超平面的距离刚好为 1。
最终,间隔变成:
Distance = 1 ∥ w ∥ \text{Distance} =\frac{1}{\|w\|} Distance=∥w∥1
4. 优化目标
SVM 的目标是最大化间隔,即最小化 ( ∥ w ∥ ( \|w\| (∥w∥)。因此,我们的优化问题可以写为:
min w , b 1 2 ∥ w ∥ 2 \min_{w, b} \frac{1}{2} \|w\|^2 w,bmin21∥w∥2
同时,约束条件是所有样本点要被正确分类,即:
y i ( w T x i + b ) ≥ 1 ∀ i y_i (w^T x_i + b) \geq 1 \quad \forall i yi(wTxi+b)≥1∀i
这是一个凸二次优化问题,能够通过拉格朗日乘子法和对偶问题来求解。
3、凸优化问题
将支持向量机(SVM)的优化问题转换为对偶问题,主要是通过拉格朗日乘子法来处理约束条件。下面是详细步骤:
1. 原始优化问题
我们从 SVM 的原始优化问题开始。SVM 的目的是找到一个超平面 ( w T x + b = 0 ( w^T x + b = 0 (wTx+b=0) 来分隔两个类别,同时最大化间隔。原始问题为:
优化目标
min w , b 1 2 ∥ w ∥ 2 \min_{w, b} \frac{1}{2} \|w\|^2 w,bmin21∥w∥2
约束条件
y i ( w T x i + b ) ≥ 1 ∀ i y_i (w^T x_i + b) \geq 1 \quad \forall i yi(wTxi+b)≥1∀i
2. 拉格朗日乘子法
为了将此问题转换为对偶问题,我们引入拉格朗日乘子 ( α i ≥ 0 ( \alpha_i \geq 0 (αi≥0),为每个约束 ( y i ( w T x i + b ) − 1 ≥ 0 ( y_i (w^T x_i + b) - 1 \geq 0 (yi(wTxi+b)−1≥0) 对应一个拉格朗日乘子。原始的拉格朗日函数 ( L ( w , b , α ) ( L(w, b, \alpha) (L(w,b,α)) 为:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 n α i [ y i ( w T x i + b ) − 1 ] L(w, b, \alpha) = \frac{1}{2} \|w\|^2 - \sum_{i=1}^n \alpha_i \left[ y_i (w^T x_i + b) - 1 \right] L(w,b,α)=21∥w∥2−i=1∑nαi[yi(wTxi+b)−1]
其中:
- ( α i ≥ 0 ( \alpha_i \geq 0 (αi≥0) 是拉格朗日乘子,对应于每个约束。
3. 拉格朗日函数分析
拉格朗日函数 ( L ( w , b , α ) ( L(w, b, \alpha) (L(w,b,α)) 包含两个部分:
- 第一部分是目标函数 ( 1 2 ∥ w ∥ 2 ( \frac{1}{2} \|w\|^2 (21∥w∥2),它希望最小化法向量的模,等价于最大化间隔。
- 第二部分包含所有约束的乘积,确保分类正确。
为了求解这个优化问题,我们需要同时最小化 w w w 和 b b b(主问题),并且最大化 α \alpha α(对偶问题)。
4. 求解对 w w w 和 b b b 的极值
接下来,我们对 w w w 和 b b b 进行最小化。首先对 w w w 求偏导数,并令其等于 0:
∂ L ( w , b , α ) ∂ w = w − ∑ i = 1 n α i y i x i = 0 \frac{\partial L(w, b, \alpha)}{\partial w} = w - \sum_{i=1}^n \alpha_i y_i x_i = 0 ∂w∂L(w,b,α)=w−i=1∑nαiyixi=0
得到:
w = ∑ i = 1 n α i y i x i w = \sum_{i=1}^n \alpha_i y_i x_i w=i=1∑nαiyixi
这表明,最终的法向量 w w w 是支持向量的线性组合。
然后对 b b b 求偏导数,并令其等于 0:
∂ L ( w , b , α ) ∂ b = ∑ i = 1 n α i y i = 0 \frac{\partial L(w, b, \alpha)}{\partial b} = \sum_{i=1}^n \alpha_i y_i = 0 ∂b∂L(w,b,α)=i=1∑nαiyi=0
因此,我们得到一个约束条件:
∑ i = 1 n α i y i = 0 \sum_{i=1}^n \alpha_i y_i = 0 i=1∑nαiyi=0
5. 构造对偶问题
现在,我们将 w w w的表达式 ( w = ∑ i = 1 n α i y i x i ( w = \sum_{i=1}^n \alpha_i y_i x_i (w=∑i=1nαiyixi) 代入到拉格朗日函数中,消去 w w w:
将 ( w = ∑ i = 1 n α i y i x i ( w = \sum_{i=1}^n \alpha_i y_i x_i (w=∑i=1nαiyixi) 代入到 ( 1 2 ∥ w ∥ 2 ( \frac{1}{2} \|w\|^2 (21∥w∥2) 中:
1 2 ∥ w ∥ 2 = 1 2 ( ∑ i = 1 n α i y i x i ) T ( ∑ j = 1 n α j y j x j ) = 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j x i T x j \frac{1}{2} \|w\|^2 = \frac{1}{2} \left( \sum_{i=1}^n \alpha_i y_i x_i \right)^T \left( \sum_{j=1}^n \alpha_j y_j x_j \right) = \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j x_i^T x_j 21∥w∥2=21(i=1∑nαiyixi)T(j=1∑nαjyjxj)=21i=1∑nj=1∑nαiαjyiyjxiTxj
然后,我们将 w w w的表达式代入拉格朗日函数的第二项:
− ∑ i = 1 n α i [ y i ( w T x i + b ) − 1 ] = − ∑ i = 1 n α i y i ( ∑ j = 1 n α j y j x j T x i ) + ∑ i = 1 n α i y i b + ∑ i = 1 n α i -\sum_{i=1}^n \alpha_i \left[ y_i (w^T x_i + b) - 1 \right] = - \sum_{i=1}^n \alpha_i y_i \left( \sum_{j=1}^n \alpha_j y_j x_j^T x_i \right)+\sum_{i=1}^n \alpha_i y_i b+\sum_{i=1}^n \alpha_i −i=1∑nαi[yi(wTxi+b)−1]=−i=1∑nαiyi(j=1∑nαjyjxjTxi)+i=1∑nαiyib+i=1∑nαi
由上述约束条件:
∑ i = 1 n α i y i = 0 \sum_{i=1}^n \alpha_i y_i = 0 i=1∑nαiyi=0
得到对偶问题的优化目标:
max α ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j x i T x j \max_{\alpha} \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j x_i^T x_j αmaxi=1∑nαi−21i=1∑nj=1∑nαiαjyiyjxiTxj
对偶问题的约束条件:
- ( α i ≥ 0 ( \alpha_i \geq 0 (αi≥0)
- ( ∑ i = 1 n α i y i = 0 ( \sum_{i=1}^n \alpha_i y_i = 0 (∑i=1nαiyi=0)
通过求解这个对偶问题,我们可以得到每个样本对应的拉格朗日乘子 ( α i ( \alpha_i (αi)。再根据 ( α i ( \alpha_i (αi) 的值,求得 w w w 和 b b b,从而得到最终的分类决策函数。
在支持向量机(SVM)的对偶问题求解完成后,拉格朗日乘子 α i \alpha_i αi 的解已经找到。通过这些解,我们可以计算出权重向量 w w w。不过,我们仍需要求解偏置项 b b b,它是决策边界的偏移量。
6、通过支持向量求解 b b b
由于 b b b出现在 SVM 的决策函数 g ( x ) = w T x + b g(x) = w^T x + b g(x)=wTx+b中,求解 b b b 时我们需要利用支持向量。支持向量是那些位于边界上的训练样本,即它们满足 y i ( w T x i + b ) = 1 y_i (w^T x_i + b) = 1 yi(wTxi+b)=1。支持向量对应的拉格朗日乘子 α i > 0 \alpha_i > 0 αi>0,而其他样本的 α i = 0 \alpha_i = 0 αi=0。
我们可以通过任意一个支持向量的公式来求解 b b b。
支持向量的条件
对于支持向量 x i x_i xi,有:
y i ( w T x i + b ) = 1 y_i (w^T x_i + b) = 1 yi(wTxi+b)=1
将 w w w 的表达式 w = ∑ j = 1 n α j y j x j w = \sum_{j=1}^n \alpha_j y_j x_j w=∑j=1nαjyjxj 代入上式(别忘了,我们有 ( y i ∈ { − 1 , 1 } ( y_i \in \{-1, 1\} (yi∈{−1,1})):
y i ( ∑ j = 1 n α j y j x j T x i + b ) = 1 y_i \left( \sum_{j=1}^n \alpha_j y_j x_j^T x_i + b \right) = 1 yi(j=1∑nαjyjxjTxi+b)=1
化简得:
∑ j = 1 n α j y j x j T x i + b = y i \sum_{j=1}^n \alpha_j y_j x_j^T x_i + b = y_i j=1∑nαjyjxjTxi+b=yi
从这里我们可以解出 b b b:
b = y i − ∑ j = 1 n α j y j x j T x i b = y_i - \sum_{j=1}^n \alpha_j y_j x_j^T x_i b=yi−j=1∑nαjyjxjTxi
要计算 b b b,我们只需要找到一个支持向量 x i x_i xi,然后将其代入上述公式即可。更一般地,我们也可以使用多个支持向量的平均值来求解 b b b,以提高计算的稳定性。具体步骤如下:
- 选择多个支持向量:这些支持向量是满足 α i > 0 \alpha_i > 0 αi>0 的样本点。
- 代入求 b b b 的公式:
- 对每一个支持向量 x i x_i xi,我们可以使用公式:
b = y i − ∑ j = 1 n α j y j x j T x i b = y_i - \sum_{j=1}^n \alpha_j y_j x_j^T x_i b=yi−j=1∑nαjyjxjTxi - 若选择多个支持向量,可以取它们对应的 b b b 的平均值:
b = 1 m ∑ i ∈ S V ( y i − ∑ j = 1 n α j y j x j T x i ) b = \frac{1}{m} \sum_{i \in SV} \left( y_i - \sum_{j=1}^n \alpha_j y_j x_j^T x_i \right) b=m1i∈SV∑(yi−j=1∑nαjyjxjTxi)
其中, S V SV SV表示支持向量的集合, m m m 是支持向量的个数。
- 对每一个支持向量 x i x_i xi,我们可以使用公式:
7. 对偶问题的解法
通过求解上述的对偶优化问题,我们可以得到拉格朗日乘子 ( α i ( \alpha_i (αi)。找到最优解后,法向量 w w w可以由支持向量(那些 ( α i > 0 ( \alpha_i > 0 (αi>0))的线性组合表示为:
w = ∑ i = 1 n α i y i x i w = \sum_{i=1}^n \alpha_i y_i x_i w=i=1∑nαiyixi
代入 g ( x ) = w T x + b g(x)=w^T x + b g(x)=wTx+b,最终用于分类的决策函数为:
f ( x ) = sign ( ∑ i = 1 n α i y i x i T x + b ) f(x) = \text{sign}\left(\sum_{i=1}^n \alpha_i y_i x_i^T x + b \right) f(x)=sign(i=1∑nαiyixiTx+b)
其中 b b b可以通过支持向量求得。
4、非线性如何划分
支持向量机(SVM)通过一种称为核技巧(Kernel Trick)的方法来处理非线性数据。基本思想是:将原始的输入数据从低维的非线性可分空间映射到高维空间,在这个高维空间中,数据变得线性可分,然后再使用线性SVM进行分类。具体步骤和方法如下:
1. 非线性数据问题
在原始空间中,SVM只能找到一个线性超平面来分割数据。然而,很多数据集是非线性可分的,线性分类器在这些情况下无法取得好的效果。例如:
- 数据在二维平面中是非线性分布的,例如以圆形或螺旋形方式分布。
- 线性SVM无法找到一个直线或平面来正确分类这些数据。
为了解决这个问题,SVM需要将原始数据映射到一个更高的维度,在这个高维空间中,数据可能就变得线性可分了。
2. 核技巧的核心思想
SVM 并不直接将数据映射到高维空间,而是通过使用一种称为核函数(Kernel Function)的方法,避免实际地进行高维计算。核函数能够计算两个样本在高维空间中的内积,而无需显式地进行高维映射。
SVM 的优化问题依赖于样本之间的内积(即 ( x i ⋅ x j ( x_i \cdot x_j (xi⋅xj)),我们可以通过核函数来计算这个内积:
K ( x i , x j ) = ϕ ( x i ) T ϕ ( x j ) K(x_i, x_j) = \phi(x_i)^T \phi(x_j) K(xi,xj)=ϕ(xi)Tϕ(xj)
其中:
- x i x_i xi 和 x j x_j xj 是原始空间中的样本。
- ϕ ( x ) \phi(x) ϕ(x) 是将 x x x 从原始空间映射到高维空间的映射函数。
- K ( x i , x j ) K(x_i, x_j) K(xi,xj) 是核函数,它计算了 x i x_i xi 和 x j x_j xj 在高维空间中的内积。
通过使用核函数,我们可以在不显式进行高维映射的情况下,计算出在高维空间中样本之间的内积,从而利用线性SVM进行分类。
3. 常见的核函数
SVM 使用核函数来替代直接的内积计算,不同的核函数对应于不同的高维映射。常见的核函数有:
1. 线性核(Linear Kernel)
K ( x i , x j ) = x i T x j K(x_i, x_j) = x_i^T x_j K(xi,xj)=xiTxj
这个核函数表示在原始空间中不进行任何映射,直接应用线性SVM。适用于数据已经线性可分的情况。
2. 多项式核(Polynomial Kernel)
K ( x i , x j ) = ( x i T x j + c ) d K(x_i, x_j) = (x_i^T x_j + c)^d K(xi,xj)=(xiTxj+c)d
这个核函数将数据映射到高维多项式空间,适用于非线性关系可以用多项式模型表示的情况。
- c c c 是常数(通常 c ≥ 0 c \geq 0 c≥0)。
- d d d 是多项式的阶数,控制映射的维度。
3. 高斯径向基核(RBF Kernel)/ 高斯核
K ( x i , x j ) = exp ( − ∥ x i − x j ∥ 2 2 σ 2 ) K(x_i, x_j) = \exp\left( -\frac{\|x_i - x_j\|^2}{2\sigma^2} \right) K(xi,xj)=exp(−2σ2∥xi−xj∥2)
RBF 核将数据映射到无限维的空间,适用于各种非线性数据。它非常灵活且常用于实际问题中。 σ \sigma σ 控制高斯函数的宽度,决定了每个数据点的“影响范围”。
4. Sigmoid 核(类似于神经网络的激活函数)
K ( x i , x j ) = tanh ( κ x i T x j + c ) K(x_i, x_j) = \tanh(\kappa x_i^T x_j + c) K(xi,xj)=tanh(κxiTxj+c)
Sigmoid 核在某些情况下类似于神经网络中的一个激活函数,适用于神经网络相关的任务。
4. 使用核技巧的 SVM 优化问题
使用核函数后,SVM 的优化目标和对偶问题发生了一些变化。原始的对偶优化问题依赖于样本之间的内积 ( x i ⋅ x j ( x_i \cdot x_j (xi⋅xj),现在变为依赖于核函数:
对偶优化目标:
max α ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j K ( x i , x j ) \max_{\alpha} \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j K(x_i, x_j) αmaxi=1∑nαi−21i=1∑nj=1∑nαiαjyiyjK(xi,xj)
约束条件:
- α i ≥ 0 \alpha_i \geq 0 αi≥0
- ∑ i = 1 n α i y i = 0 \sum_{i=1}^n \alpha_i y_i = 0 ∑i=1nαiyi=0
在这里,内积 x i T x j x_i^T x_j xiTxj 被核函数 K ( x i , x j ) K(x_i, x_j) K(xi,xj) 替代。因此,在高维空间中的优化依然是线性问题,但是通过核函数的作用,解决了原始空间中的非线性问题。
5. SVM 的决策函数
训练完成后,SVM 的分类决策函数也依赖于核函数,表示为:
f ( x ) = ∑ i = 1 n α i y i K ( x i , x ) + b f(x) = \sum_{i=1}^n \alpha_i y_i K(x_i, x) + b f(x)=i=1∑nαiyiK(xi,x)+b
其中, α i \alpha_i αi 是拉格朗日乘子, K ( x i , x ) K(x_i, x) K(xi,x) 是核函数,它计算新样本 x x x 与训练样本 x i x_i xi 的相似度。
- 如果使用线性核,这个决策函数就等价于线性SVM。
- 如果使用非线性核(例如 RBF 核),决策函数将是一种非线性分类器。
6. 核函数的选择
选择合适的核函数对于非线性问题的解决至关重要:
- 线性核适用于线性可分或接近线性可分的数据。
- 多项式核适用于多项式关系较强的数据,但阶数 d d d 需要调节。
- RBF 核是最常用的核函数之一,它可以很好地处理复杂的非线性数据。
- Sigmoid 核与神经网络类似,在特定应用中有时会使用,但不如 RBF 核普遍。
即使有了核函数,支持向量机(SVM)仍需要引入软间隔和正则化,以增强对噪声和不可分数据的鲁棒性。以下是引入软间隔和正则化的原因及其对应的数学推导和原理。
5、软间隔
虽然通过核函数可以将非线性数据映射到高维空间,并且使其在高维空间中线性可分,但在实际数据集中,有噪声的样本或错误标注的样本可能无法被完全正确分类。因此,直接使用一个完全的线性可分分类器(硬间隔SVM)可能会导致以下问题:
- 过拟合:当分类器过于严格地尝试将所有样本分类正确时,它可能会对数据中的噪声过于敏感,从而对训练数据过拟合,无法很好地泛化到新的数据。
- 无法处理不可分数据:某些数据集中,数据点在高维空间中依然不是完全线性可分的,硬间隔SVM无法找到一个有效的超平面来区分这些数据。
因此,引入软间隔(Soft Margin)是为了允许某些样本可以违反分类间隔要求,以提高模型的鲁棒性,并控制模型的复杂度,避免过拟合。
1、允许部分错误分类
为了应对上述问题,SVM 引入了软间隔的概念。软间隔允许一些样本违反间隔条件,即允许它们出现在错误的一侧,或者没有完全位于正确的边界上。为此,我们引入松弛变量(slack variables) ξ i \xi_i ξi 来表示每个样本违反间隔的程度。
软间隔 SVM 的目标函数和约束条件
在软间隔 SVM 中,优化问题变为在保持最大间隔的同时,允许一定的分类错误。引入松弛变量后的优化问题可以表示为:
目标函数:
min w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 n ξ i \min_{w, b, \xi} \ \frac{1}{2} \|w\|^2 + C \sum_{i=1}^n \xi_i w,b,ξmin 21∥w∥2+Ci=1∑nξi
其中:
- 1 2 ∥ w ∥ 2 \frac{1}{2} \|w\|^2 21∥w∥2 是与硬间隔 SVM 一致的间隔最大化目标。
- C ∑ i = 1 n ξ i C \sum_{i=1}^n \xi_i C∑i=1nξi 是为了惩罚违反间隔的样本, ξ i ≥ 0 \xi_i \geq 0 ξi≥0 表示第 i i i 个样本的松弛程度。
- C C C 是一个正则化参数,用来控制模型在最大间隔和分类错误之间的权衡。较大的 C C C 倾向于减少分类错误,较小的 C C C 则允许更多分类错误,从而使间隔更大。
约束条件:
y i ( w T x i + b ) ≥ 1 − ξ i ∀ i y_i (w^T x_i + b) \geq 1 - \xi_i \quad \forall i yi(wTxi+b)≥1−ξi∀i
和
ξ i ≥ 0 ∀ i \xi_i \geq 0 \quad \forall i ξi≥0∀i
这里, y i ( w T x i + b ) ≥ 1 − ξ i y_i (w^T x_i + b) \geq 1 - \xi_i yi(wTxi+b)≥1−ξi 意味着每个样本的分类间隔必须至少为 1 − ξ i 1 - \xi_i 1−ξi,并且 ξ i \xi_i ξi 是允许间隔违背的程度。当 ξ i = 0 \xi_i = 0 ξi=0 时,样本严格满足分类间隔条件;当 ξ i > 0 \xi_i > 0 ξi>0 时,样本位于间隔内部或被错误分类。
6、正则化:控制模型的复杂度
在软间隔 SVM 中,正则化通过引入参数 C C C 来控制模型的复杂度。它的作用是调整间隔最大化和分类错误之间的权衡。
C C C 的影响:
- 较大的 C C C:表示对分类错误的惩罚更大,因此模型会更严格地尝试将每个样本正确分类,但可能导致过拟合,因为它会对噪声样本过于敏感。
- 较小的 C C C:表示对分类错误的容忍度更高,因此模型会允许更多样本违反分类间隔,间隔可能更大,但泛化能力更强。
正则化在数学上通过目标函数中的 ( C ∑ i = 1 n ξ i ( C \sum_{i=1}^n \xi_i (C∑i=1nξi) 项来实现。此项增加了对违反分类间隔样本的惩罚,并且通过调节 ( C ) 的值来调整对错误分类的容忍度。
7、软间隔和核函数结合
即使引入了核函数来处理非线性数据,仍然有必要使用软间隔和正则化。原因是即便数据被映射到高维空间,有些数据仍可能不完全线性可分,或者存在噪声样本,这些噪声样本可能导致分类器出现过拟合。因此,结合核函数和软间隔可以增强分类器的泛化能力。
使用核函数的软间隔 SVM 优化目标
我们现在将核函数引入到软间隔 SVM 的对偶问题中。对偶问题的形式与原始 SVM 相似,但会包含惩罚项 C C C。
对偶优化问题
max α ∑ i = 1 n α i − 1 2 ∑ i = 1 n ∑ j = 1 n α i α j y i y j K ( x i , x j ) \max_{\alpha} \sum_{i=1}^n \alpha_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j K(x_i, x_j) αmaxi=1∑nαi−21i=1∑nj=1∑nαiαjyiyjK(xi,xj)
约束条件
- 0 ≤ α i ≤ C 0 \leq \alpha_i \leq C 0≤αi≤C
- ∑ i = 1 n α i y i = 0 \sum_{i=1}^n \alpha_i y_i = 0 ∑i=1nαiyi=0
这里的 α i \alpha_i αi 是拉格朗日乘子, K ( x i , x j ) K(x_i, x_j) K(xi,xj) 是核函数。 0 ≤ α i ≤ C 0 \leq \alpha_i \leq C 0≤αi≤C 这一约束表明拉格朗日乘子不再无限制,受正则化参数 ( C ) 的影响。
相关文章:

支持向量机SVM原理详解
SVM原理详解 1、超平面2、SVM原理1. 问题定义2. 分类决策得到约束条件 3. 最大化间隔4. 优化目标 3、凸优化问题1. 原始优化问题优化目标约束条件 2. 拉格朗日乘子法3. 拉格朗日函数分析4. 求解对 w w w 和 b b b 的极值5. 构造对偶问题对偶问题的约束条件: 6、通…...
使用JMeter进行Spring Boot接口的压力测试
使用 Apache JMeter 对接口进行压力测试是一个相对简单的过程。以下是详细的步骤,包括安装、配置和执行测试计划。 1. 下载和安装 JMeter 下载 JMeter 从 JMeter 官方网站https://jmeter.apache.org/download_jmeter.cgi 下载最新版本的 JMeter。 解压缩 将下载的 …...
---- 尊重父类(1))
C++学习笔记----9、发现继承的技巧(三)---- 尊重父类(1)
当写继承类的时候,需要清楚父类与子类之间的交互。像生成顺序,构造函数链,以及转化都可以是问题的根源。 1、父类构造函数 对象不会马上就能干活;它们必须由父类以及所包含的任意对象进行构建。c定义了如下的生成顺序:…...

启动service报错ORA-44317: database open read-only
ADG(RAC)备库环境,srvctl添加service服务成功,启动service时报错ORA-44317: database open read-only。 这是预期行为, 使用“srvctl add service -d <db_name> -s <service_name>”创建服务时,…...

GNU/Linux - Savannah项目
* 我们托管在自由操作系统上运行的自由项目,不依赖任何专有软件。 * 我们的服务使用 100% 的自由软件运行,包括服务本身。 * We host free projects that run on free operating systems and without any proprietary software dependencies. * Our se…...

Debug-028-el-carousel走马灯-当展示图片为2的问题处理
前言: el-carousel走马灯又是给elementui填坑的一天。el-carousel走马灯其实类似小程序中的轮播图。这里担心涉及版权问题就不贴项目中的图了。简单阐述一下问题:正常使用el-carousel时,如果图片数量大于等于3时,可以定时自动顺序…...
)
TapData 知识库 | 一文吃透数据整合(Data Consolidation)
顾名思义,数据整合指的是将不同来源的数据汇集在一起,并将其集中存储于一个统一的数据平台。数据整合使用户能够通过单一访问入口获取数据,进而推动数据洞察的生成与分析。 数据通常被简单地看作信息的集合,仿佛默认每个数据单元在…...

MySQL数据的导出
【图书推荐】《MySQL 9从入门到性能优化(视频教学版)》-CSDN博客 《MySQL 9从入门到性能优化(视频教学版)(数据库技术丛书)》(王英英)【摘要 书评 试读】- 京东图书 (jd.com) MySQL9数据库技术_夏天又到了…...
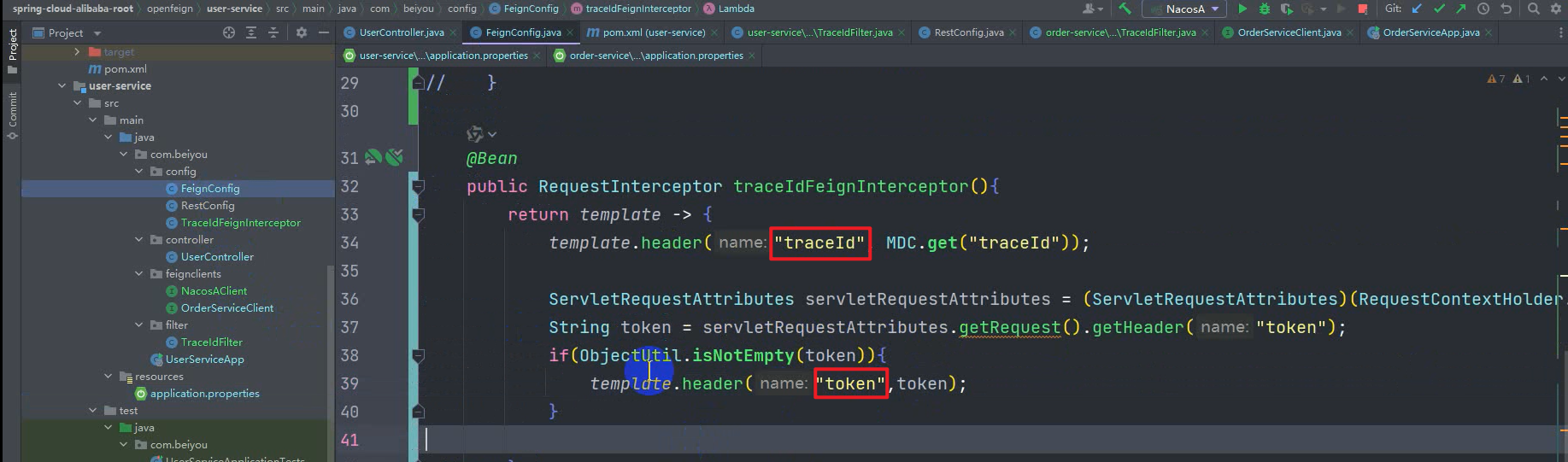
微服务--OpenFeign【重点】
如果哪天 我们硬编码写的接口变了,只要写过该接口的 都要改,太麻烦了, 所以 就用 OpenFeign 来解决这个麻烦 了解: SimpleClientHttpRequestFactory和 HttpComponentsClientHttpRequestFactory 都是Spring框架中用于创建ClientH…...

【力扣打卡系列】滑动窗口与双指针(两数之和)
坚持按题型打卡&刷&梳理力扣算法题系列,语言为go,Day1 两数之和 题目描述 解题思路 采用哈希表 将nums[i] nums[j] target 转化成 nums[i] target - nums[j]去思考新建一个map来存储,键为值(左边的)&#…...

蚂蚁华东师范大学:从零开始学习定义和解决一般优化问题LLMOPT
🎯 推荐指数:🌟🌟🌟 📖 title:LLMOPT: Learning to Define and Solve General Optimization Problems from Scratch 🔥 code:https://github.com/caigaojiang/LLMOPT &am…...

价格游戏的终章:品牌如何在通货膨胀时代智取市场
来源:The era of price-led profit growth is coming to an end (marketingweek.com) 近年来,通货膨胀促使许多品牌通过提价来提升利润,而销量几乎没有受到太大影响。然而,随着通货膨胀放缓,继续提价的策略可能会吸引…...

CVTE Android面试题及参考答案
Activity 的生命周期 Activity 的生命周期分为以下几个主要状态: onCreate ():在 Activity 第一次被创建的时候调用。通常在这个方法中进行一些初始化操作,如设置布局、初始化成员变量等。这是 Activity 进入可见状态的第一步。onStart ():当 Activity 即将对用户可见的时候…...

Docker实战:从入门到进阶
Docker实战:从入门到进阶 引言 Docker是一个开源的应用容器引擎,它允许开发者打包他们的应用以及应用的依赖包到一个可移植的容器中,然后发布到任何支持Docker的平台上。本文将通过实战和应用举例,带领大家深入了解Docker的强大…...

Jupyter Notebook汉化(中文版)
原版jupyter notebook是英文的,想要将其改为中文 在jupyter notebook所在环境输入以下命令 pip install jupyterlab-language-pack-zh-CN打开jupyter notebook,在设置语言中将其设置为中文...

C#的小数位保留以及四舍五入
C#使用Math.Round("数值","保留位","保留方式")进行小数位保留以及四舍五入 //1.MidpointRounding.ToEven(四舍六入五成双) //当保留小数位后一位为0~4时,舍去末位 var x1 Math.Round(1.124, 2, MidpointRo…...

KNNImputer
KNNImputer实例是指在使用Python的scikit-learn库时,通过sklearn.impute.KNNImputer类创建的一个对象,该对象专门用于处理数据集中的缺失值。KNNImputer采用K-近邻(K-Nearest Neighbors,KNN)算法来估算并填充这些缺失值…...

RHCE例行性工作笔记
1、单一执行的例行性工作 单一执行的例行性工作: 仅处理执行一次就结束了 at命令的工作过程 /etc/at.allow ,写在该文件的人可以使用 at 命令 /etc/at.deny ,黑名单 两个文件如果都不存在,只有 root 能使用 #at 工作调度对应的…...

ros2 action server示例、拓展、练习
注意:以下代码全部由ai生成,没有大问题,运用时需根据报错逐步调试 action server示例 将 goal、result 和 feedback 作为类的成员变量的 C 示例代码: 示例代码 #include "rclcpp/rclcpp.hpp" #include "rclcpp…...

【Go语言】安装及使用基础教程
文章目录 1. 下载安装Go官网安装使用 Homebrew 安装 (Mac)创建工作目录 (Workspace)设置环境变量通过 VSCode 扩展商店安装 Go 插件处理权限问题 2. Hello, World 示例3. 语法基础变量声明常量数组切片(Slice)Map(集合)控制结构fo…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...
