【LeetCode】动态规划—96. 不同的二叉搜索树(附完整Python/C++代码)
动态规划—96. 不同的二叉搜索树
- 题目描述
- 前言
- 基本思路
- 1. 问题定义
- 2. 理解问题和递推关系
- 二叉搜索树的性质:
- 核心思路:
- 状态定义:
- 状态转移方程:
- 边界条件:
- 3. 解决方法
- 动态规划方法:
- 伪代码:
- 4. 进一步优化
- 5. 小总结
- Python代码
- Python代码解释
- C++代码
- C++代码解释
- 总结
题目描述

前言
不同的二叉搜索树问题 是一个经典的动态规划问题。给定一个整数 n,我们需要构造出由 n 个节点组成的所有不同的 二叉搜索树(BST)。在这类问题中,我们不仅需要理解二叉搜索树的性质,还需要通过动态规划来计算不同形态的二叉搜索树的数量。
基本思路
1. 问题定义
给定一个整数 n,求由 n 个节点构成的所有不同的二叉搜索树的数量。每个二叉搜索树的节点包含从 1 到 n 的整数,每个整数只能使用一次。
2. 理解问题和递推关系
二叉搜索树的性质:
- 二叉搜索树(BST)的性质是,对于每个节点:
- 左子树上所有节点的值都小于该节点的值。
- 右子树上所有节点的值都大于该节点的值。
核心思路:
如果我们选择节点 i 作为根节点,那么:
- 节点
1到i-1会组成根节点i的左子树。 - 节点
i+1到n会组成根节点i的右子树。 - 左子树和右子树的组合方式可以递归地进行计算,最终组合成完整的 BST。
状态定义:
设 dp[i] 表示 i 个节点能构成的不同二叉搜索树的数量。最终我们要求解的是 dp[n]。
状态转移方程:
对于每一个根节点 i,它的左子树有 i-1 个节点,右子树有 n-i 个节点。左子树和右子树的组合方式相乘,即:
d p [ i ] = ∑ k = 1 i d p [ k − 1 ] × d p [ i − k ] dp[i] = \sum_{k=1}^{i} dp[k-1] \times dp[i-k] dp[i]=k=1∑idp[k−1]×dp[i−k]
其中,dp[k-1] 表示左子树的组合数,dp[i-k] 表示右子树的组合数。
边界条件:
- 当
n = 0时,空树也是一种二叉搜索树,因此dp[0] = 1。
3. 解决方法
动态规划方法:
- 初始化一个数组
dp,其中dp[0] = 1,表示空树。 - 使用递推公式计算
dp[i],即根据左子树和右子树的组合方式来更新dp数组。 - 最终
dp[n]即为n个节点构成的不同二叉搜索树的数量。
伪代码:
initialize dp array with dp[0] = 1
for i from 1 to n:for j from 1 to i:dp[i] += dp[j-1] * dp[i-j]
return dp[n]
4. 进一步优化
- 空间优化:由于每个
dp[i]只依赖于之前的状态,因此我们已经使用最小的空间来存储这些状态。 - 时间复杂度:动态规划的时间复杂度为
O(n^2),适合处理中等规模的输入。
5. 小总结
- 问题思路:通过递归地构建左子树和右子树,利用动态规划的思想,可以高效计算不同二叉搜索树的数量。
- 核心公式:状态转移方程
dp[i] = \sum_{k=1}^{i} dp[k-1] \times dp[i-k],每次通过左子树和右子树的组合方式进行计算。
以上就是不同的二叉搜索树问题的基本思路。
Python代码
class Solution:def numTrees(self, n: int) -> int:# 初始化dp数组,dp[i]表示i个节点能构成的不同二叉搜索树的数量dp = [0] * (n + 1)dp[0] = 1 # 空树也是一种二叉搜索树# 动态规划计算每个dp[i]的值for i in range(1, n + 1):for j in range(1, i + 1):dp[i] += dp[j - 1] * dp[i - j]return dp[n] # 返回n个节点能构成的不同二叉搜索树的数量
Python代码解释
- 初始化:定义一个
dp数组,dp[i]表示i个节点能构成的不同二叉搜索树的数量。初始值dp[0] = 1,表示空树。 - 动态规划递推:使用状态转移公式更新
dp数组,每次根据左子树和右子树的组合方式来累加。 - 返回结果:返回
dp[n],即n个节点可以构成的不同二叉搜索树的数量。
C++代码
class Solution {
public:int numTrees(int n) {// 初始化dp数组,dp[i]表示i个节点能构成的不同二叉搜索树的数量vector<int> dp(n + 1, 0);dp[0] = 1; // 空树也是一种二叉搜索树// 动态规划计算每个dp[i]的值for (int i = 1; i <= n; ++i) {for (int j = 1; j <= i; ++j) {dp[i] += dp[j - 1] * dp[i - j];}}return dp[n]; // 返回n个节点能构成的不同二叉搜索树的数量}
};
C++代码解释
- 初始化:定义一个
dp数组,dp[i]表示i个节点能构成的不同二叉搜索树的数量。初始值dp[0] = 1,表示空树。 - 动态规划递推:使用状态转移公式更新
dp数组,每次根据左子树和右子树的组合方式来累加。 - 返回结果:返回
dp[n],即n个节点可以构成的不同二叉搜索树的数量。
总结
- 核心思路:通过递归构建不同的左子树和右子树,利用动态规划求解不同二叉搜索树的数量。每一个根节点的左子树和右子树的组合数相乘即为该根节点对应的不同二叉搜索树的数量。
- 时间复杂度:时间复杂度为
O(n^2),适合处理中等规模的输入。 - 动态规划应用:该问题展示了动态规划在树形结构问题中的应用,通过递推和组合的方式有效解决了求解二叉搜索树数量的问题。
相关文章:

【LeetCode】动态规划—96. 不同的二叉搜索树(附完整Python/C++代码)
动态规划—96. 不同的二叉搜索树 题目描述前言基本思路1. 问题定义2. 理解问题和递推关系二叉搜索树的性质:核心思路:状态定义:状态转移方程:边界条件: 3. 解决方法动态规划方法:伪代码: 4. 进一…...
Nginx UI 一个可以管理Nginx的图形化界面工具
Nginx UI 是一个基于 Web 的图形界面管理工具,支持对 Nginx 的各项配置和状态进行直观的操作和监控。 Nginx UI 的功能非常丰富: 在线查看服务器 CPU、内存、系统负载、磁盘使用率等指标 在线 ChatGPT 助理 一键申请和自动续签 Let’s encrypt 证书 在…...

Vue向上滚动加载数据时防止内容闪动
目前的需求:当前组件向上滚动加载数据,dom加载完后,页面的元素位置不能发生变化 遇到的问题:加载完数据后,又把滚轮滚到之前记录的位置时,内容发生闪动 现在的方案: 加载数据之前记录整体滚动条…...

基于QT、ARM的智能停车管理系统+高分项目+源码
Parking-management-system 本系统基于QT、ARM开发板、Linux系统并对接百度AI 1.1 项目目的: 创建一个智能停车管理系统,能够停入车辆和取出车辆以及查询车辆停入停车场的状态并且计算车辆离开时收费情况。 1.2 项目意义: 实现停车场智能抬杆和智能收费系统&…...

1.6,unity动画Animator屏蔽某个部位,动画组合
动画组合 一边跑一边攻击 using System.Collections; using System.Collections.Generic; using UnityEngine;public class One : MonoBehaviour {private Animator anim;// Start is called before the first frame updatevoid Start(){anim GetComponent<Animator>();…...

发动机冷却系统排空气
发动机冷却系统排空气的几种常见方法 发动机冷却系统是汽车发动机的重要组成部分,它的主要作用是通过循环冷却液来吸收和散发发动机产生的热量,确保发动机在正常工作温度下运行。然而,在冷却系统的运行过程中,由于各种原因&#…...

三周精通FastAPI:1 第一步入门
FastAPI是一个非常棒的python web和api框架,准备用三周的时间“精通它” 学习流程参考FastAPI官网的用户教程:教程 - 用户指南 - FastAPI 学前提示 运行代码 所有代码片段都可以复制后直接使用(它们实际上是经过测试的 Python 文件&#x…...

RestTemplate基本使用之HTTP实现GET请求和POST请求
一、GET请求实例 public static TianQi getTianQi(String city) {RestTemplate restTemplate new RestTemplate();HashMap res restTemplate.getForObject("http://www.tianqiapi.com/api/?versionv6&appid15118158&appsecretgVNnwva8&city" city, H…...

2024-10-18 问AI: [AI面试题] 神经网络有哪些不同类型?
文心一言 神经网络有多种不同类型,每种类型都有其特定的结构和应用场景。以下是一些主要的神经网络类型: 前馈神经网络(FNN): 也称为全连接神经网络或感知器网络。由输入层、隐藏层和输出层组成,信息流是单…...

【开源免费】基于SpringBoot+Vue.JS课程作业管理系统(JAVA毕业设计)
本文项目编号 T 023 ,文末自助获取源码 \color{red}{T023,文末自助获取源码} T023,文末自助获取源码 目录 一、系统介绍二、演示录屏三、启动教程四、功能截图五、文案资料5.1 选题背景5.2 国内外研究现状5.3 可行性分析 六、核心代码6.1 查…...

jmeter中对于有中文内容的csv文件怎么保存
jmeter的功能很强大,但是细节处没把握好就得不到预期的结果。今天来讲讲有中文内容的csv文件的参数化使用中需要注意的事项。 对于有中文内容,涉及到编码格式,为了让jmeter能正确地读取csv文件中的中文,需要把文件转码为UTF-8BOM…...

Leetcode 921 Shortest Path in Binary Matrix
题意:求二维矩阵中往8个方向移动的话,从左上方到右下方移动的最短路径 https://leetcode.com/problems/shortest-path-in-binary-matrix/description/ 解答:bfs易得 class Solution { public:int shortestPathBinaryMatrix(vector<vecto…...

第二十二篇——菲欧几何:相对论的数学基础是什么?
目录 一、背景介绍二、思路&方案三、过程1.思维导图2.文章中经典的句子理解3.学习之后对于投资市场的理解4.通过这篇文章结合我知道的东西我能想到什么? 四、总结五、升华 一、背景介绍 对于几何的几个工具,让我再次感叹数学的伟大,逻辑…...

【AI整合包及教程】EchoMimic:开创数字人新时代,让静态图像“活”起来!
在数字化浪潮的推动下,人工智能技术正以前所未有的速度渗透到我们生活的方方面面。从智能家居到自动驾驶,从智能客服到医疗诊断,AI的触角无处不在。而如今,阿里巴巴旗下的蚂蚁集团再次引领潮流,宣布开源其革命性的数字…...

ArcGIS 最新底图服务地址
ArcGIS 最新底图服务地址 说明 先上地址: 地形图: https://services.arcgisonline.com/arcgis/rest/services/Elevation/World_Hillshade/MapServer深色地形图:https://services.arcgisonline.com/arcgis/rest/services/Elevation/World_Hi…...

【服务器部署】Docker部署小程序
一、下载Docker 安装之前,一定查看是否安装docker,如果有,卸载老版本 我是虚拟机装的Centos7,linux 3.10 内核,docker官方说至少3.8以上,建议3.10以上(ubuntu下要linux内核3.8以上,…...
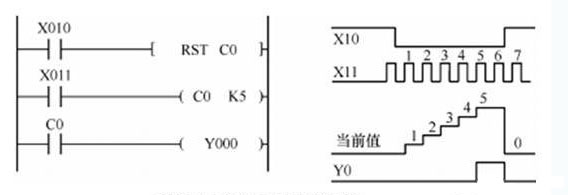
三菱FX PLC设计一个电子钟程序实例
在这里介绍三菱FX系列PLC的计数器C的功能、结构,计数过程及工作原理。 功能: 对内部元件X、Y、M、S、T、C的信号进行计数。 结构: 线圈、触点、设定值寄存器、当前值寄存器。 地址编号: 字母C+(…...

妇女、商业与法律(WBL)(1971-2023年)
WBL项目由世界银行开发,旨在通过分析时间序列数据,研究女性机会不平等与劳动市场动态之间的关系。该项目提供了1971年至2023年的190个经济体的面板数据,包括8个评分指标和35个数据点,涵盖了流动性、工作场所、薪酬、婚姻、父母身份…...

python 卸载、安装、virtualenv
前言 本文汇总下python环境的安装与卸载。 卸载python环境 卸载系统环境内的python环境 python_version_number3.10 sudo rm -rf /Library/Frameworks/Python.framework/Versions/${python_version_number}/ sudo rm -rf "/Applications/Python ${python_version_numb…...

ubuntu24.0离线安装Ollama和纯cpu版本以及对接Spring AI
文章目录 一.官网下载 0.3.13版本二.将文件包上传至ubuntu服务器三.下载安装脚本四.剔除GPU相关下载ROCM等,纯CPU运行脚本五.ollama常用命令六. 远程测试 七.对接spring AI 一.官网下载 0.3.13版本 ollama离线安装包下载地址 二.将文件包上传至ubuntu服务器 三.下…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
