强化学习的数学原理-01基本概念
state: T h e s t a t u s o f a g e n t w i t h r e s p e c t t o t h e e n v i r o n m e n t The \quad status \quad of \quad agent \quad with \quad respect \quad to \quad the \quad environment Thestatusofagentwithrespecttotheenvironment (agent 相对于环境的状态)
对于下面的网格地图来说: s t a t e state state就相当于$ location $,用 s 1 、 s 2 、 . . . 、 s 9 s_1、s_2、...、s_9 s1、s2、...、s9来表示
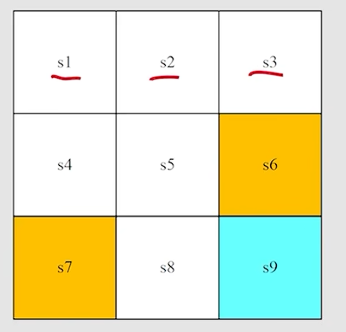
state space: T h e s e t o f a l l s t a t e S = { s i } i = 1 9 The \quad set \quad of \quad all \quad state \quad S = \{s_i\}_{i=1}^{9} ThesetofallstateS={si}i=19 状态空间,把所有 s t a t e state state放在一起得到的集合就是 s t a t e s p a c e state \quad space statespace
Action: F o r e a c h s t a t e , t h e r e a r e f i v e p o s s i b l e a c t o i n : a 1 、 a 2 、 a 3 、 a 4 、 a 5 For \quad each \quad state, \quad there \quad are \quad five \quad possible \quad actoin: a_1、a_2、a_3、a_4、a_5 Foreachstate,therearefivepossibleactoin:a1、a2、a3、a4、a5
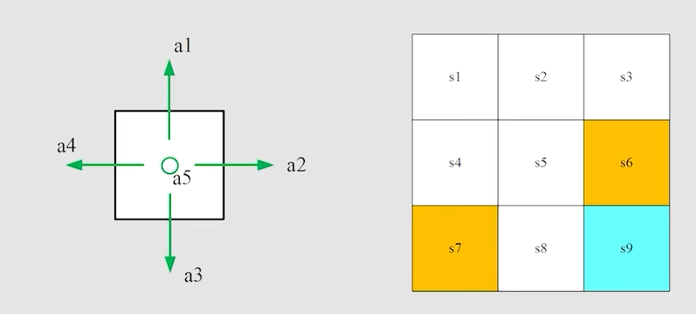
Action space of a state: t h e s e t o f a l l p o s s i b l e a c t i o n s o f a q u a d s t a t e the \quad set \quad of \quad all possible actions \quad of \quad a \ quad state thesetofallpossibleactionsofa quadstate
A ( s i ) = { a i } i = 1 5 A(s_i) = \{a_i\}_{i=1}^{5} A(si)={ai}i=15
state transition: 当采取了一个 a c t i o n action action后, a g e n t agent agent从一个 s t a t e state state转移到另一个 s t a t e state state,这样一个过程佳作 s t a t e t r a n s i t i o n state \quad transition statetransition

s t a t e t r a n s i t i o n state \quad transition statetransition定义一种 a g e n t agent agent和 e n v i r o n m e n t environment environment交互的行为
Forbidden area:有两种情况,一种是forbidden are可以到达,但是会得到相应的惩罚,另一种是forbidden area不可到达,相当于有一堵墙。
Tabular representation:可以用表格来描述state transition
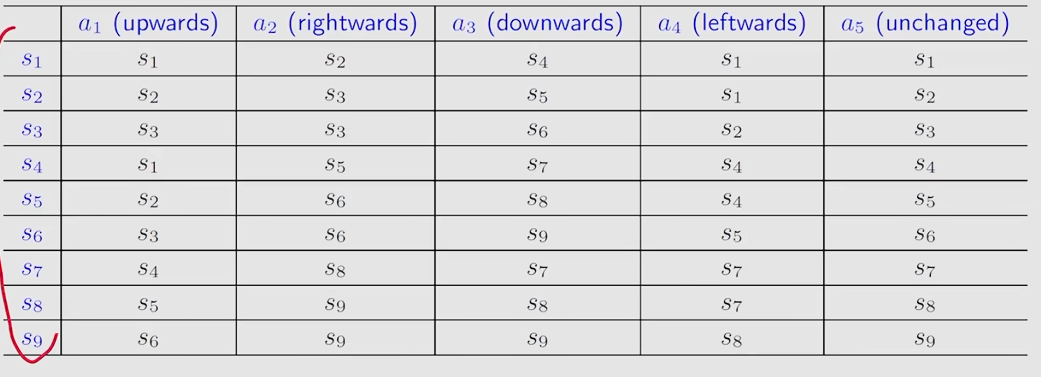
只能能表示确定的情况
相比于上面的表格,更一般的做法是使用下面这种方法
state transition probability:使用概率来描述state transition

Policy:告诉agent在一个状态应该采取什么动作
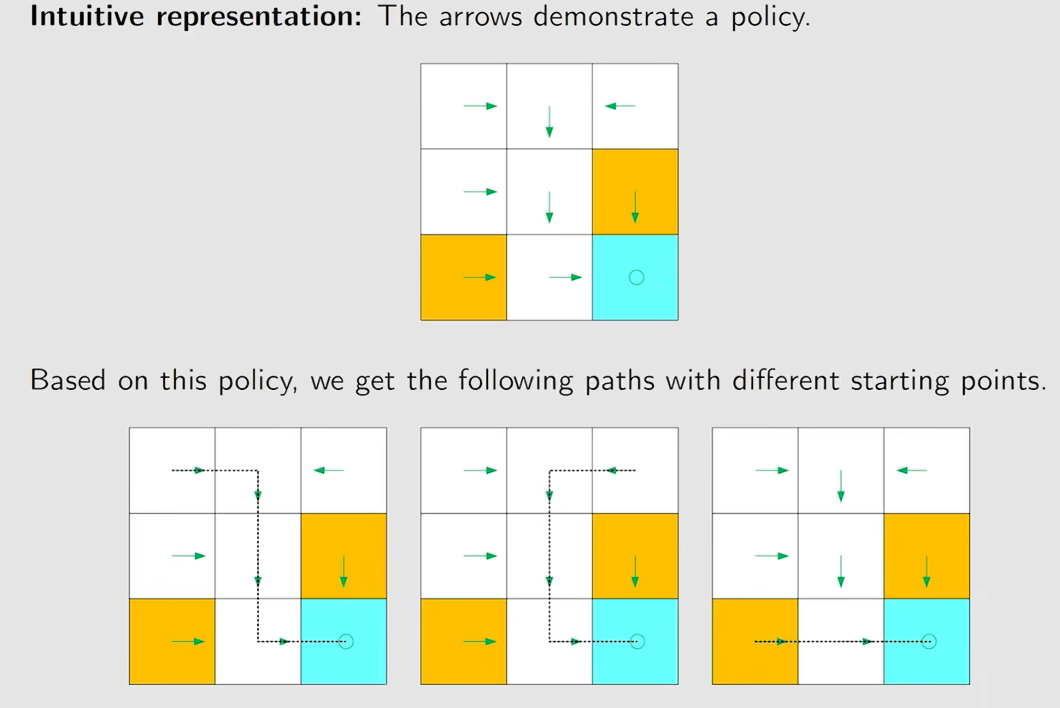

π \pi π在强化学习中用来表示条件概率,而不是圆周率
上面图片中的情况是确定性的策略,同时也有不确定的策略
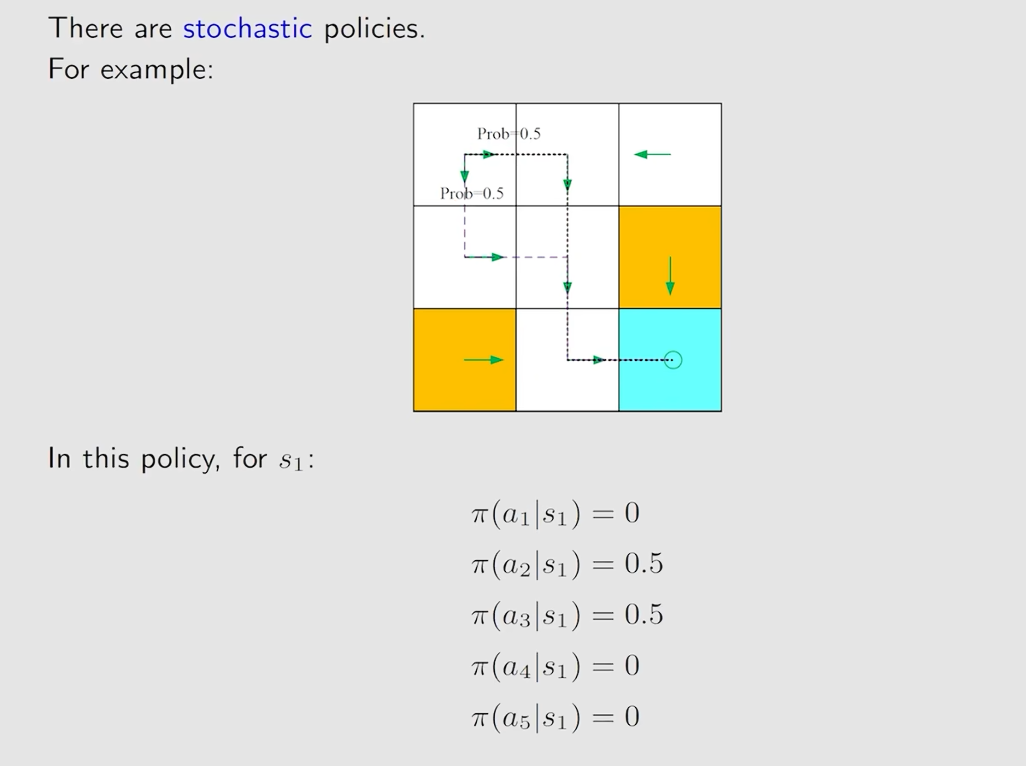
Reward:reward是action采取一个action后得到的实数,一个正的reward代表鼓励采取这样的action,一个负的reward代表惩罚这样的action。
reward可以理解成一个 h u m a n − m a c h i n e i n t e r f a c e human-machine \quad interface human−machineinterface,我们人类和机器交互的一个接口
reward依赖于当前的 s t a t e 和采取的 a c t i o n state和采取的action state和采取的action而不是依赖于接下来的 s t a t e state state
trajectory:是一个 s t a t e − a c t i o n − r e w a r d state-action-reward state−action−reward chain
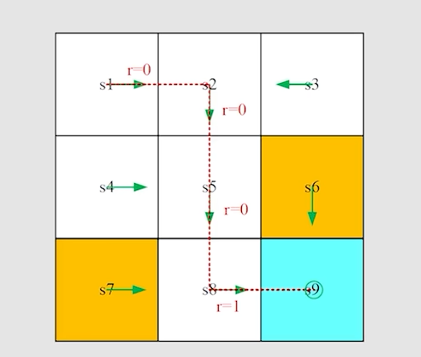
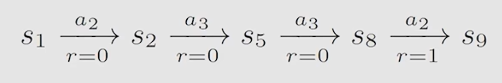
Return:沿着trajectory,所有的reward相加得到得就是return
return的作用可以用来评估一个策略的好坏
discount return:
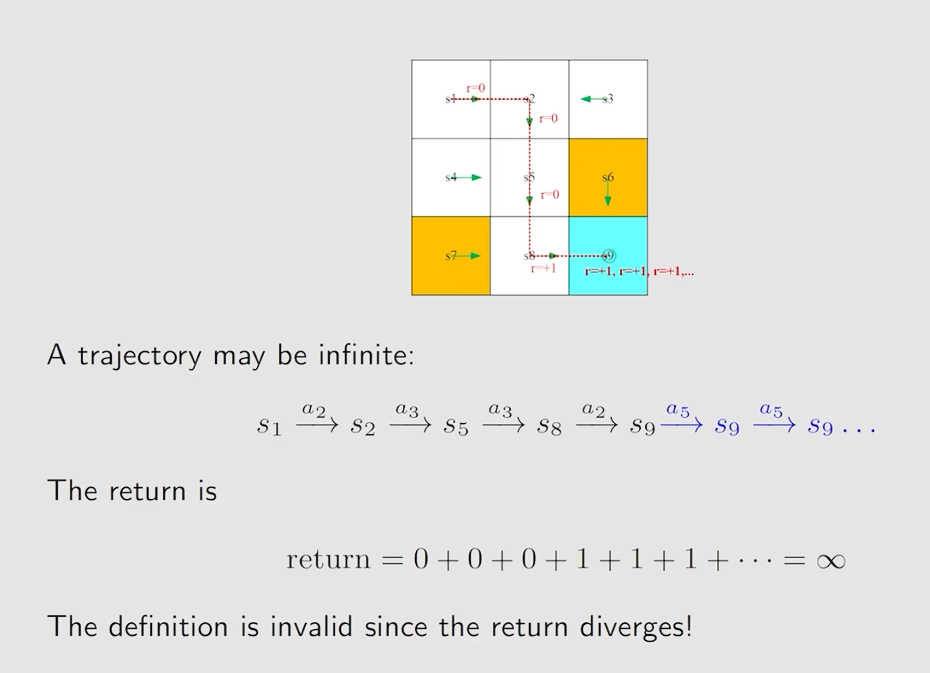
从上图可以看到上面的trajectory是无限长的,对应的return是发散的。
为了解决这个问题引入一个 d i s c o u n t r a t e γ ∈ [ 0 , 1 ) discount \quad rate \quad \gamma \in [0, 1) discountrateγ∈[0,1)
上面的return就可以用discount return来表示
$discount return = 0 + \gamma * 0 + {\gamma^2} * 0 + {\gamma^3} * 1 + {\gamma^4} * 1 + … $
d i s c o u n t r e t u r n = γ 3 ( 1 + γ + γ 2 + γ 3 + . . . ) discount return = \gamma^3(1 + \gamma + \gamma^2 + \gamma^3 + ...) discountreturn=γ3(1+γ+γ2+γ3+...)
d i s c o u n t r e t u r n = γ 3 ( 1 1 − γ ) discount return = \gamma^3(\frac{1}{1 - \gamma}) discountreturn=γ3(1−γ1)
episode\trial:一个有限步的trajectory被称为episode,也就是有terminal states的trajectory。
可以采用方法将episodic转化为continue的,在terminal state时无论采取什么action都会回到terminal state。
MDP:Markov decision process,马尔可夫决策过程是一个框架framework
一个马尔可夫决策过程中有很多关键的元素:
set:
- State:
- Action
- Reward
Probability distribution:
- State transition probability:在一个状态s,采取action a,转移到状态 s ′ s^{'} s′的概率 p ( s ′ ∣ s , a ) p(s^{'}|s,a) p(s′∣s,a)
- Reward probability:在状态s,采取action a,得到reward r的概率 p ( r ∣ s , a ) p(r|s, a) p(r∣s,a)
Policy:
在状态s,采取action a的概率 π ( a ∣ s ) \pi(a|s) π(a∣s)
Markov property:memoryless property

相关文章:

强化学习的数学原理-01基本概念
state: T h e s t a t u s o f a g e n t w i t h r e s p e c t t o t h e e n v i r o n m e n t The \quad status \quad of \quad agent \quad with \quad respect \quad to \quad the \quad environment Thestatusofagentwithrespecttotheenvironment (agent 相对于环境的…...
D41【python 接口自动化学习】- python基础之函数
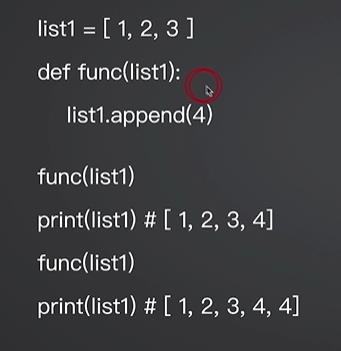
day41 函数参数传递错误 学习日期:20241018 学习目标:函数﹣-54 避坑指南:列表作为参数传递出错了怎么办? 学习笔记: 列表类型的特殊性 list1[x,y,z] tuple1(list1,b,c)# 修改元组中的列表,会…...

思迅商云8修改最大找零金额
执行如下语句前请备份数据库 -POS收银找零金额最大数 --把下面SQL中的 1000.00 改成你想要的金额数,再到查询分析器中执行: --总店 use hbposv8 go insert t_sys_system (sys_var_id, sys_var_value, sys_var_name) values (pos_max_givchg, 1000.00, 最…...

Lumerical学习——分析工具(Analysis tools)
一、分析工具和模拟环境(Analysis tools and the simulation environment) 模拟计算完成后,模拟计算数据紧接着写到模拟工程文件中;甚至当模拟计算提前结束时计算得到的部分数据集也会写到文件中。当模拟完成后单击退出按钮、或者…...

思迅商云8会员积分全部清0
请您备份数据库后执行以下语句: declare card_id varchar(20), acc_num numeric(16,4), dec_num numeric(16,4), minus_num numeric(16,4), branch_no varchar(4), count int select branch_nosys_var_value fro…...

$nextTick原理
一、什么是 $nextTick $nextTick 是 Vue 实例上的一个方法,允许我们在下次 DOM 更新循环结束后执行一个回调。这通常用于需要访问更新后的 DOM状态的场景。由于 Vue 在数据变化后并不会立即更新 DOM,而是进行异步批处理,使用 $nextTick可以保…...

python办公:批量PDF合并—通用版
目录 专栏导读1、库的介绍2、库的安装3、核心代码3、提供测试PDF生成代码5、完整代码进阶版总结 专栏导读 🌸 欢迎来到Python办公自动化专栏—Python处理办公问题,解放您的双手 🏳️🌈 博客主页:请点击——> 一…...

人工智能研究创造出新型蛋白质
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

blender 金币基站 建模 学习笔记
一、学习blender视频教程链接 案例3:金币基站_建模_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1Bt4y1E7qn?vd_sourced0ea58f1127eed138a4ba5421c577eb1&p12&spm_id_from333.788.videopod.episodes 二、金币基站建模过程 (1&#x…...

eggjs sequelize egg-sequelize-auto自动从零生成一个数据表 自动创建model
sequelize egg-sequelize-auto整个过程还是有一些坑 包括兼容性问题 依赖安装问题 需要注意 缺少一个条件 包跑不起来 或使用体验很差 1. 全局安装插件 pnpm install -g sequelize-cli sequelize mysql2 egg-sequelize-auto 2. 执行命令创建 migrate迁移文件 以及 mod…...

解决低版本pytorch和onnx组合时torch.atan2()不被onnx支持的问题
解决这个问题,最简单的当然是升级pytorch和onnx到比较高的版本,例如有人验证过的组合: pytorch2.1.1cu118, onnxruntime1.16.3 但是因为你的模型或cuda环境等约束,不能安装这么高的版本的pytorch和onnx组合时(例如我的环境是pytorch1.12&…...

javaWeb项目-ssm+jsp房屋出租管理系统功能介绍
本项目源码(点击下方链接下载):java-ssmjsp房屋出租管理系统实现源码(项目源码-说明文档)资源-CSDN文库 项目关键技术 开发工具:IDEA 、Eclipse 编程语言: Java 数据库: MySQL5.7 框架:ssm、Springboot 前端ÿ…...

【R语言】gadm全球行政区划数据库
我R语言不熟、也不是学GIS的。仅用于记录。 文章目录 一、gadm 数据库简介二、R 语言示例三、sf 包的函数 一、gadm 数据库简介 GADM(全称Database of Global Administrative Areas)是一个高精度的全球行政区划数据库,它包含了全球所有国家和…...
)
3万字66道Java基础面试题总结(2024版本)
本文合计三万字,整合了66道当前Java面试中比较热门的面试题,希望对大家有所帮助。 文章目录 一、Java概念1. JDK和JRE和JVM的区别2. Java语言有哪些特点3. 什么是字节码?采用字节码的最大好处是什么?4. Oracle JDK 和 OpenJDK 的对…...

go 环境安装
最近搭建AIGC大模型聚合平台,涉及到了go语言,随手整理一下环境安装步骤分享给大家。 1、安装 官网下载地址:https://go.dev/ 1.1 Linux 安装 yum install git -y yum install golang -y yum install gcc -y # 日志工具,如需要…...

stereo-seq 细胞、捕获到的分子及其特征的统计描述
Cell Count、Mean/Median Cell Area、Mean/Median DNB Count、Mean/Median Gene Type、Mean/Median MID 这些术语与空间转录组学和单细胞测序等技术中的细胞和基因表达数据分析有关。每个指标都是对细胞、捕获到的分子及其特征的统计描述。以下是每个术语的详细解释: 1. Cell…...

ceph rook-ceph 部署 cephobjectstore 失败
版本信息 helm list WARNING: Kubernetes configuration file is group-readable. This is insecure. Location: /Users/zld/kubeconfigs/gir.yaml WARNING: Kubernetes configuration file is world-readable. This is insecure. Location: /Users/zld/kubeconfigs/gir.yaml …...
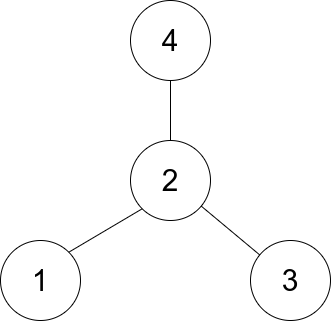
1791. 找出星型图的中心节点
有一个无向的 星型 图,由 n 个编号从 1 到 n 的节点组成。星型图有一个 中心 节点,并且恰有 n - 1 条边将中心节点与其他每个节点连接起来。 给你一个二维整数数组 edges ,其中 edges[i] [ui, vi] 表示在节点 ui 和 vi 之间存在一条边。请你…...

微调小型Llama 3.2(十亿参数)模型取代GPT-4o
微调Llama VS GPT-4o 别忘了关注作者,关注后您会变得更聪明,不关注就只能靠颜值了 ^_^。 一位年轻的儿科医生与一位经验丰富的医师,谁更能有效治疗婴儿的咳嗽? 两者都具备治疗咳嗽的能力,但儿科医生由于专攻儿童医学…...

【JavaEE】【IO】文件操作
目录 一、文件1.1 文件的概念1.2 文件的操作1.3 路径1.4 文件分类 二、Java中的文件元信息、路径操作2.1 属性2.2 构造方法2.3 方法2.3.1 文件路径2.3.2 文件判断2.3.3 文件创建删除2.3.4 其他操作 三、文件读写操作3.1 流(Stream)3.1.1 字节流3.1.1.1 I…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

pycharm 设置环境出错
pycharm 设置环境出错 pycharm 新建项目,设置虚拟环境,出错 pycharm 出错 Cannot open Local Failed to start [powershell.exe, -NoExit, -ExecutionPolicy, Bypass, -File, C:\Program Files\JetBrains\PyCharm 2024.1.3\plugins\terminal\shell-int…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...
