AtCoder Beginner Contest 375 A-E 题解
我的老师让我先做最后再交,看正确率(即以OI赛制打abc)
所以我用的小号(… …)
C 卡了老半天才出来,我把题读错了

难度:
A. Seats
题意
给你一个字符串 S S S,仅包含 . 和 #,找出子串 #.# 的个数
思路
若下标从 0 0 0 开始,直接枚举 i ∈ [ 0 , n − 3 ] i\in [0,n-3] i∈[0,n−3] 即可
C++ 代码
#include<bits/stdc++.h>
using namespace std;
int n;
string s;
int ans;
int main(){cin>>n>>s;for(int i=0;i<n-2;i++){if(s[i]=='#'&&s[i+1]=='.'&&s[i+2]=='#'){ans++;}}cout<<ans<<endl;return 0;
}
B. Traveling Takahashi Problem
题意
给你平面上的 n n n 个点,第 i i i 个点坐标为 ( x i , y i ) (x_i,y_i) (xi,yi),现在需要从原点 ( 0 , 0 ) (0,0) (0,0) 出发,按顺序经过每个点,并回到原点 ( 0 , 0 ) (0,0) (0,0),问最终走过的距离。
注:从 ( x i , y i ) (x_i,y_i) (xi,yi) 到 ( x j , y j ) (x_j,y_j) (xj,yj) 的距离是 ( x j − x i ) 2 + ( y j − y i ) 2 \sqrt{(x_j-x_i)^2+(y_j-y_i)^2} (xj−xi)2+(yj−yi)2
思路
记录上次停留的位置,按顺序模拟即可
C++ 代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
long double ans;
int n;
int sqr(int x){return x*x;
}
signed main(){cin>>n;int curx=0,cury=0;for(int i=1;i<=n;i++){int a,b;cin>>a>>b;ans+=sqrt(sqr(a-curx)+sqr(b-cury));curx=a,cury=b;}ans+=sqrt(sqr(curx)+sqr(cury));cout<<fixed<<setprecision(20)<<ans<<endl;return 0;
}
C. Spiral Rotation
题意
有一个 n ∗ n n*n n∗n 的网格( n n n 为偶数),设 ( i , j ) (i,j) (i,j) 为从上往下数第 i i i 行,从左往右数第 j j j 列的格子,每格要么是 . 要么是 #
对于 i ∈ { 1 , 2 , . . . , n / 2 } i \in \{ 1,2,\ ..., \ n/2\} i∈{1,2, ..., n/2}:
- 选择数对 ( x , y ) (x,y) (x,y) ,其中 1 ≤ x , y ≤ n + 1 − i 1\le x,y \le n+1-i 1≤x,y≤n+1−i,将 ( y , n + 1 − x ) (y,n+1-x) (y,n+1−x) 的值换为 ( x , y ) (x,y) (x,y)
- 对于所有符合要求的 ( x , y ) (x,y) (x,y),同时 进行以上操作
思路
由 $(y,n+1-x) $ = ( x , y ) (x,y) (x,y) 可得: ( i , j ) (i,j) (i,j) = ( n + 1 − j , i ) (n+1-j,i) (n+1−j,i)
那么共有以下四种情况:
-
( i , j ) = ( n + 1 − j , i ) (i,j) = (n+1-j,i) (i,j)=(n+1−j,i)
-
( n + 1 − j , i ) = ( n + 1 − i , n + 1 − j ) (n+1-j,i)=(n+1-i,n+1-j) (n+1−j,i)=(n+1−i,n+1−j)
-
( n + 1 − i , n + 1 − j ) = ( j , n + 1 − i ) (n+1-i,n+1-j)=(j,n+1-i) (n+1−i,n+1−j)=(j,n+1−i)
-
( j , n + 1 − i ) = ( i , j ) (j,n+1-i)=(i,j) (j,n+1−i)=(i,j)
-
下一次就又回到了第一种
所以只要看每一个操作了多少次 $\bmod 4 $ 的余数就可以了
C++ 代码
#include<bits/stdc++.h>
using namespace std;
string s[maxn];
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>s[i];s[i]=" "+s[i];}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){int curi=(i>k?n-i+1:i);int curj=(j>k?n-j+1:j);int cur=min(curi,curj)%4;if(cur%4==0){cout<<s[i][j];}else if(cur%4==1){cout<<s[n+1-j][i];}else if(cur%4==2){cout<<s[n+1-i][n+1-j];}else{cout<<s[j][n+1-i];}}cout<<endl;}return 0;
}
D. ABA
题意
给你一个字符串 s s s,你要选出三个下标: 1 ≤ i < j < k ≤ ∣ s ∣ 1\le i<j<k\le |s| 1≤i<j<k≤∣s∣,将 s i , s j , s k s_i, s_j,s_k si,sj,sk 拼接,使得拼接起来的字符串是 回文串
思路
对于 26 26 26 个字母,分别记录每种出现在哪些位置,再统一加减
C++ 代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
vector<int> g[26];
string s;
signed main(){int n=sz(s);s=" "+s;for(int i=1;i<=n;i++){g[s[i]-'A'].push_back(i);}int ans=0;for(int i=0;i<26;i++){if(g[i].size()==0) continue;int sum=g[i][0];for(int j=1;j<g[i].size();j++){ans+=(j*g[i][j]-sum-j);sum+=g[i][j];}}cout<<ans<<endl;return 0;
}
E. 3 Team Division
题意
共有 n n n 个人,已经分成了 3 3 3 组,第 i i i 个人在 a i a_i ai 组 ( 1 ≤ a i ≤ 3 ) (1 \le a_i \le 3) (1≤ai≤3),权值为 b i b_i bi,你可以重新分组,使得每组的 权值和 相等,且 换组的人数 最少
问最少换组的人数
思路
首先可以想到 d p [ i ] [ j ] [ k ] [ l ] dp[i][j][k][l] dp[i][j][k][l] 表示:前 i i i 个里面,第一组权值和为 j j j,第二组权值和为 k k k ,第三组权值和为 l l l
那么如何优化?去掉最后一维
因为前 i i i 个人权值和一定,所以直接用总和减去 j + k j+k j+k 就得到了 l l l
C++ 代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int inf=2e15;
const int maxn=105;
const int maxk=1505;
int n;
int pos[maxn],v[maxn];
int dp[maxn][maxk][maxk];
int sum[maxn];
signed main(){cin>>n;for(int i=1;i<=n;i++){cin>>pos[i]>>v[i];sum[i]=sum[i-1]+v[i]; //计算前缀和}if(sum[n]%3!=0){//特判:只有和为3的倍数才能分成3组cout<<-1<<endl;return;}for(int i=0;i<=n;i++){//初始化dp数组for(int j=0;j<=sum[i];j++){for(int k=0;k<=sum[i]-j;k++){dp[i][j][k]=inf;}}}dp[0][0][0]=0;for(int i=1;i<=n;i++){for(int j=0;j<=sum[i];j++){for(int k=0;k<=sum[i]-j;k++){if(j>=v[i]){dp[i][j][k]=min(dp[i-1][j-v[i]][k]+(pos[i]!=1),dp[i][j][k]);}if(k>=v[i]){dp[i][j][k]=min(dp[i-1][j][k-v[i]]+(pos[i]!=2),dp[i][j][k]);}if(sum[i]-j-k>=v[i]){dp[i][j][k]=min(dp[i-1][j][k]+(pos[i]!=3),dp[i][j][k]);}}}}int ans=dp[n][sum[n]/3][sum[n]/3];if(ans==inf){cout<<-1<<endl;}else{cout<<ans<<endl;}return 0;
}
相关文章:

AtCoder Beginner Contest 375 A-E 题解
我的老师让我先做最后再交,看正确率(即以OI赛制打abc) 所以我用的小号(… …) C 卡了老半天才出来,我把题读错了 难度: A. Seats 题意 给你一个字符串 S S S,仅包含 . 和 #&…...

其他-自己手动更换汽车电磁进排气阀0.9.2
其他-自己手动更换汽车电磁进排气阀0.9.0 背景本次工具流程注意参考 2024年10月18日08:57:00—0.9.2 背景 昨天手动更换了电磁阀,记录下过程和注意事项,简单总结了一下 本次工具 10号套筒和工具老虎钳锤子一字改刀新的进排气电磁阀 流程 打开引擎盖…...
生成模型初认识
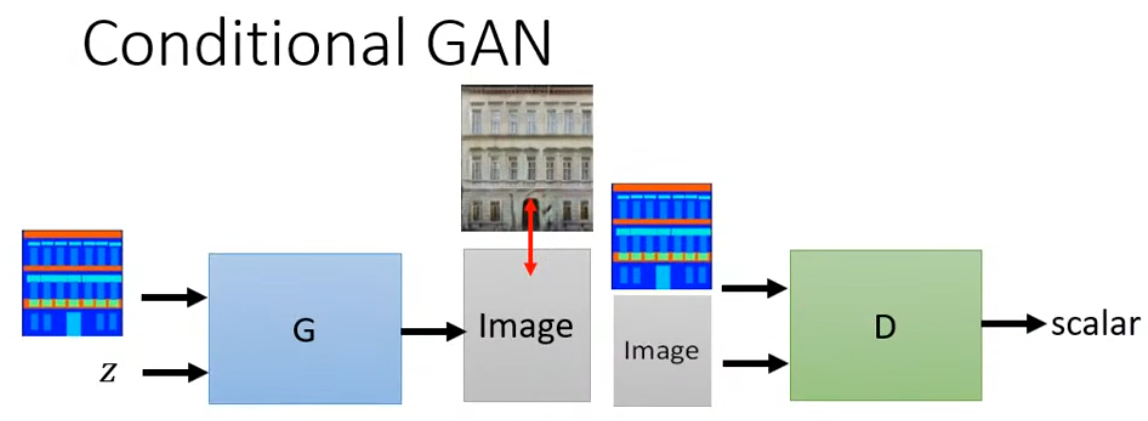
生成模型初认识 参考学习资料:李宏毅-机器学习 以下为课程过程中的简易笔记 生成模型 为什么要用生成模型?——创造力:同一个输入,产生不同的输出(distribution),有一定概率发生某种随机事件…...

Java中的一些名词概念
**函数式接口:** 概念:一个接口中的抽象方法只有一个,那么这个接口就是一个函数式接口。形参: 形参变量是**功能函数里的变量**,只有<u>在被调用的时候才分配内存单元</u>,<u>调用结束后立即释放</u>。…...

沈阳乐晟睿浩科技有限公司:引领抖音小店迈向新纪元
在当今数字化浪潮汹涌的时代,电子商务以其独特的魅力和无限潜力,正深刻改变着人们的消费习惯与商业模式。在这场变革中,沈阳乐晟睿浩科技有限公司凭借其敏锐的市场洞察力和卓越的技术实力,成为了抖音小店领域的佼佼者,…...

[图形学]蒙特卡洛积分方法介绍及其方差计算
一、简介 本文介绍了蒙特卡洛积分算法的基本原理和其误差计算。 二、蒙特卡洛积分介绍 1. 介绍 蒙特卡洛积分算法是一种数值积分算法,用于对复杂函数进行积分。 例如,对于目标积分函数: ∫ a b f ( x ) d x (1) \int_{a}^{b}f(x)\rm{d}x…...

智慧社区Web解决方案:Spring Boot框架探索
1系统概述 1.1 研究背景 随着计算机技术的发展以及计算机网络的逐渐普及,互联网成为人们查找信息的重要场所,二十一世纪是信息的时代,所以信息的管理显得特别重要。因此,使用计算机来管理基于web的智慧社区设计与实现的相关信息成…...

基于预测算法的航班离港延误系统
毕业设计不知道做什么?想找一个结合算法与应用的项目?那你绝对不能错过这个"基于预测算法的航班离港延误系统"!✈️📊 项目简介: 这个系统专注于航班离港的延误预测,通过强大的神经网络技术对大…...

【汇编语言】寄存器(内存访问)(七)—— CPU提供的栈机制
文章目录 前言1. CPU提供的栈机制2. push指令3. 问题4. 问题的分析与解答5. pop指令结语 前言 📌 汇编语言是很多相关课程(如数据结构、操作系统、微机原理)的重要基础。但仅仅从课程的角度出发就太片面了,其实学习汇编语言可以深…...

webAPI中的节点操作、高级事件
一、节点操作 1.删除节点 node.removeChild(); 方法从node节点中删除一个子节点,返回删除的节点 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widt…...

C++内存对齐机制简介
C内存对齐机制是指数据在内存中按照特定规则进行排列,这个机制可以提高访问效率并且满足硬件访问特性。 C内存对齐机制的一些关键规则如下: 不同类型的数据在内存中的起始地址应该是其大小的倍数。比如,4字节的整型应该存放在地址是4的倍数…...

java集合进阶篇-《List集合》
个人主页→VON 收录专栏→java从入门到起飞 目录 编辑 一、前言 二、List集合简要概述 三、List集合主要函数的应用 四、List集合的遍历 五、思考 一、前言 List集合与Collection集合的相同之处还是挺多的,不过有些小细节又不太一样,其中有一个…...

FPGA图像处理之均值滤波
文章目录 一、什么是图像滤波?1.1 噪声类型1.2 滤波类型 二、均值滤波原理2.1 3*3窗口滑动过程2.2 图像扩展 三、Matlab实现均值滤波四、FPGA实现均值滤波4.1 生成 3*3 矩阵4.2 仿真3*3矩阵4.3 计算均值4.4 仿真均值滤波 一、什么是图像滤波? 图像滤波是…...

高等数学 6.2 定积分在几何学上的应用
文章目录 一、平面图形的面积1.直角坐标情形2.极坐标情形 二、体积1.旋转体体积2.平行截面面积为已知的立体的体积 三、平面曲线的弧长 一、平面图形的面积 1.直角坐标情形 我们已经知道,由曲线 y f ( x ) ( f ( x ) ⩾ 0 ) y f(x) (f(x) \geqslant 0) yf(x)(f…...

缓存常见问题:缓存穿透、雪崩、击穿及解决方案分析
1. 什么是缓存穿透,怎么解决? 缓存穿透是指用户请求的数据在缓存中不存在即没有命中,同时在数据库中也不存在,导致用户每次请求该数据都要去数据库中查询一遍。如果有恶意攻击者不断请求系统中不存在的数据,会导致短时…...

C++:拷贝构造
拷贝构造函数是参数类型为本类的引用的构造函数,它也叫复制构造函数,它只有一个参数。当没有写拷贝构造函数时,会有一个默认的拷贝构造函数。 class AA { public:AA(AA& ra){}} 那么什么时候会调用此函数呢?有以下三种情况 …...

BGP(边界网关协议)
1、网络AS(自治系统) 边界网关协议BGP(Border Gateway Protocol)是一种实现自治系统AS(Autonomous System)之间的路由可达,并选择最佳路由的距离矢量路由协议。 AS是指在一个实体管辖下的拥有…...

Spring 概念汇总
一、Spring中的依赖注入和依赖反转 依赖注入(Dependency Injection) 概念 依赖注入是一种设计模式,它允许在对象创建时将其依赖的对象传递给它,而不是让对象自己去创建或查找依赖对象。在Spring中,依赖注入是控制反转…...

快速在找到函数的实体的方法
当我们写了许多许多的函数,那我们怎么快速的找到他们呢 我们只需要按下ctrl,在点击函数名字就可以快速的找到我们想要的函数...

05 django管理系统 - 部门管理 - 修改部门
04我们已经实现了新增部门的功能,下面开始修改部门模块的实现。 按道理来说,应该是做成弹框样式的,通过ajax悄咪咪的发数据,然后更新前端数据,但是考虑到实际情况,先用页面跳转的方式实现,后面…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

五、jmeter脚本参数化
目录 1、脚本参数化 1.1 用户定义的变量 1.1.1 添加及引用方式 1.1.2 测试得出用户定义变量的特点 1.2 用户参数 1.2.1 概念 1.2.2 位置不同效果不同 1.2.3、用户参数的勾选框 - 每次迭代更新一次 总结用户定义的变量、用户参数 1.3 csv数据文件参数化 1、脚本参数化 …...
智警杯备赛--excel模块
数据透视与图表制作 创建步骤 创建 1.在Excel的插入或者数据标签页下找到数据透视表的按钮 2.将数据放进“请选择单元格区域“中,点击确定 这是最终结果,但是由于环境启不了,这里用的是自己的excel,真实的环境中的excel根据实训…...
