AcWing1027

题目重述：

题目的核心是找到一条路径的最大权值总和，但路径要从起点 (1, 1) 走到终点 (n, n)。由于两条路径分别经过不同的格子，我们可以巧妙地将问题简化为两次同时出发的路径问题。这种映射的设计让我们能够更方便地处理两条路径重叠在同一个格子的情况，同时简化状态的描述和转移过程。

同时出发的映射设计：

我们把两次路径的移动过程看作是两个角色同时出发并移动。

• 路径长度（步数）用 k 表示。
• 对于某个步数 k，两个角色分别位于 (x1, y1) 和 (x2, y2) 两个位置上。
• 因为两条路径同时出发，满足：
  $$x_1+y_1=x_2+y_2=k$$
  这说明步数 k 决定了两个角色的行列位置之间的关系。

我们只需要用 3 个状态变量来描述状态：

• k: 当前的步数（路径的长度）。
• x1: 角色 1 在当前步数下的行位置。
• x2: 角色 2 在当前步数下的行位置。

这样，位置 (y1) 和 (y2) 则可以通过 y1 = k - x1 和 y2 = k - x2 推出。

DP 状态定义：

用 f[k][x1][x2] 表示在步数 k 时，两个角色分别位于 (x1, y1) 和 (x2, y2) 位置时，能达到的最大权值总和。

重叠格子的处理：

• 两条路径走到不同的格子：
  如果两个角色的行位置不同 (x1 ≠ x2)，说明它们当前站在不同的格子上，则权值总和为：
  $$w(x1,k-x1)+w(x2,k-x2)$$

• 两条路径走到相同的格子：
  如果两个角色的行位置相同 (x1 = x2)，说明它们当前站在同一个格子上，此时我们只加一次该格子的权值：
  $$w(x1,k-x1)$$

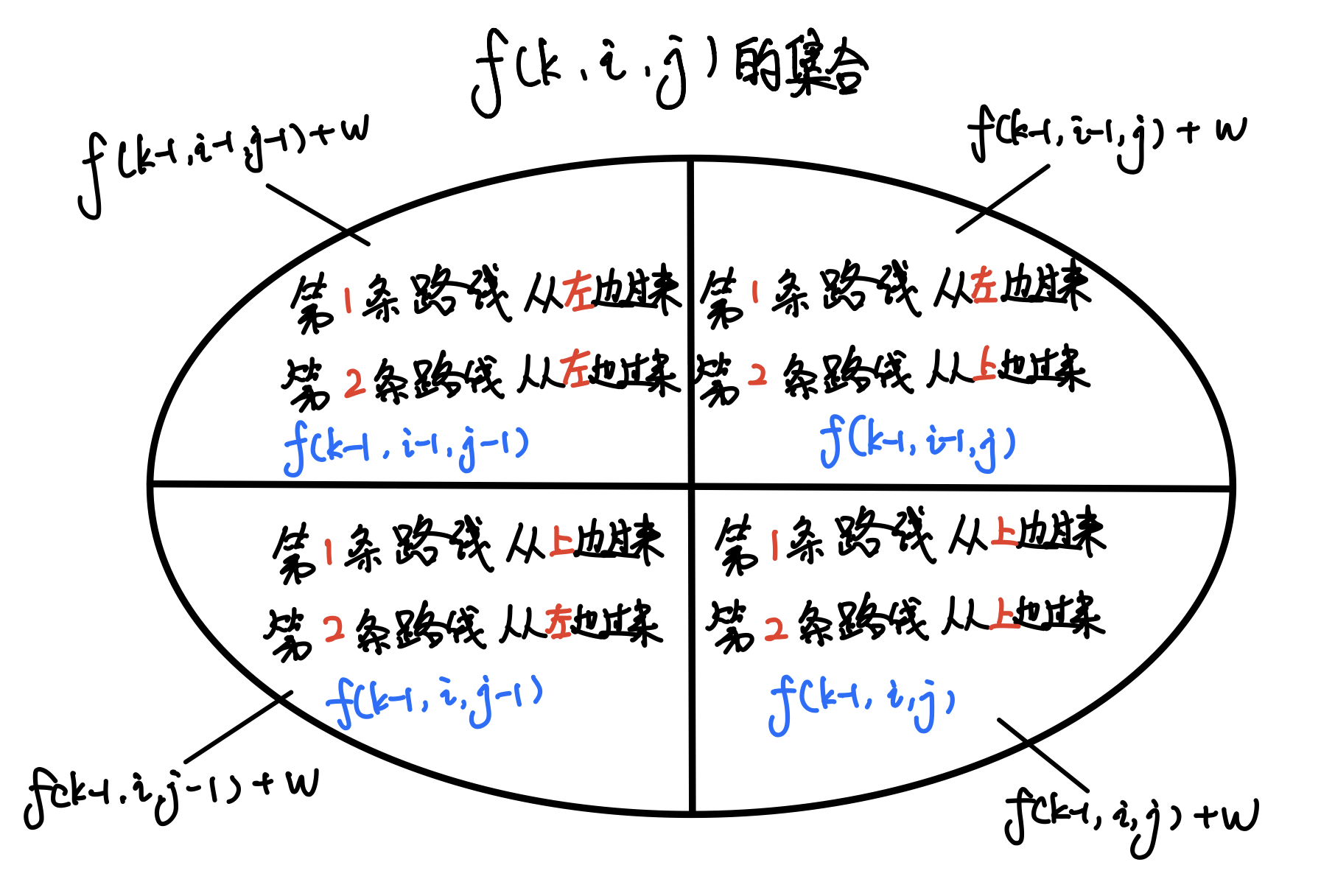
状态转移：

在步数 k 时，每个角色都有两种选择：向右走或向下走。
这导致从 k-1 时的状态到 k 时的状态共有 4 种可能的转移路径：

$$f[k][x1][x2]=\max \left\{\begin{array}{rl}& f[k-1][x1-1][x2-1],\\ & f[k-1][x1][x2-1],\\ & f[k-1][x1-1][x2],\\ & f[k-1][x1][x2]\end{array}\right\}+w$$

其中，w 的值根据上述重叠情况确定。

越界判断的必要性：

在进行状态转移时，需要保证所有涉及的状态都在合法范围内。
由于 x1 和 x2 代表行位置，所以需要确保它们不会越过棋盘边界。
即：
$$1\le x1,x2\le n\text{且}1\le y1=k-x1\le n1\le y2=k-x2\le n$$
这正是代码中越界判断的由来：

if (k - i <= 0 || k - i > n || k - j <= 0 || k - j > n) continue;

这个判断确保每个角色的当前位置都在合法范围 [1, n] 之内。否则，跳过当前状态，避免数组越界访问。

DP分析

• 初始状态：
  从起点 (1, 1) 同时出发：
  $$f[2][1][1]=w(1,1)$$

• 目标状态：
  当两条路径同时到达终点 (n, n)，即：
  $$f[2\ast n][n][n]$$
  该状态的值即为答案。

• 过程分析

  

  

代码

#include <iostream>
#include <algorithm> // 引入算法库以使用 std::maxusing namespace std;const int N = 15, M = 2 * N;int n;
int a, b, c;
int w[N][N];
int f[M][N][N];int main()
{cin >> n;while (cin >> a >> b >> c, a || b || c) w[a][b] += c;for (int k = 2; k <= 2 * n; ++k){for (int i = 1; i <= n; ++i){for (int j = 1; j <= n; ++j){if (k - i <= 0 || k - i > n || k - j <= 0 || k - j > n) continue;/*判断逻辑：这段判断确保两个角色的当前位置 (i, k - i) 和 (j, k - j) 是在有效的棋盘范围内。k - i <= 0：确保角色 1 的列位置不小于 1。k - i > n：确保角色 1 的列位置不大于 n（棋盘的边界）。k - j <= 0：确保角色 2 的列位置不小于 1。k - j > n：确保角色 2 的列位置不大于 n。如果任何一条路线越界，就执行 continue，跳过这一次的计算。*/int v = w[i][k - i];if (i != j) v += w[j][k - j];f[k][i][j] = max({f[k - 1][i - 1][j - 1], f[k - 1][i][j - 1], f[k - 1][i - 1][j], f[k - 1][i][j]}) + v;}}}cout << f[2 * n][n][n] << endl;return 0;
}

                f[k - 1][i][j]}) + v;}}
}cout << f[2 * n][n][n] << endl;
return 0;

}