图论day60|108.冗余连接（卡码网） 、109.冗余连接II（卡码网）【并查集 摧毁信心的一题，胆小的走开！】

108.冗余连接（卡码网）

题目描述

有一个图，它是一棵树，他是拥有 n 个节点（节点编号1到n）和 n - 1 条边的连通无环无向图（其实就是一个线形图），如图：

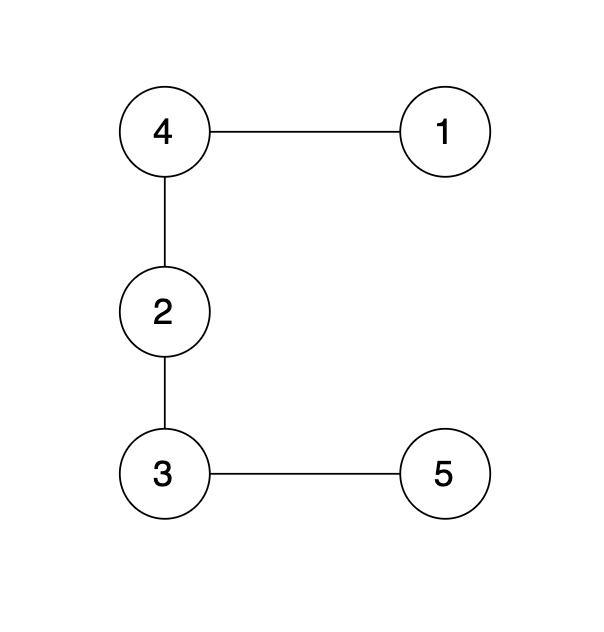
现在在这棵树上的基础上，添加一条边（依然是n个节点，但有n条边），使这个图变成了有环图，如图：

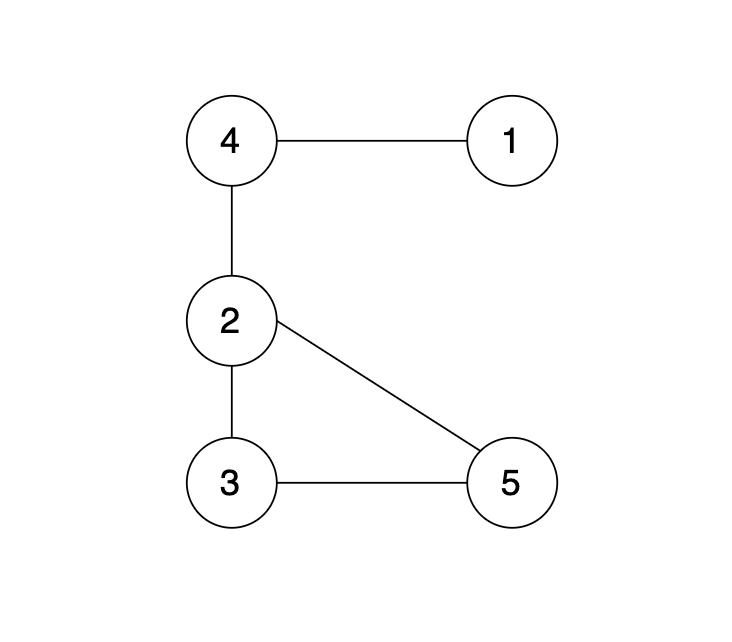
先请你找出冗余边，删除后，使该图可以重新变成一棵树。

输入描述

第一行包含一个整数 N，表示图的节点个数和边的个数。

后续 N 行，每行包含两个整数 s 和 t，表示图中 s 和 t 之间有一条边。

输出描述

输出一条可以删除的边。如果有多个答案，请删除标准输入中最后出现的那条边。

输入示例

3
1 2
2 3
1 3

输出示例

1 3

提示信息

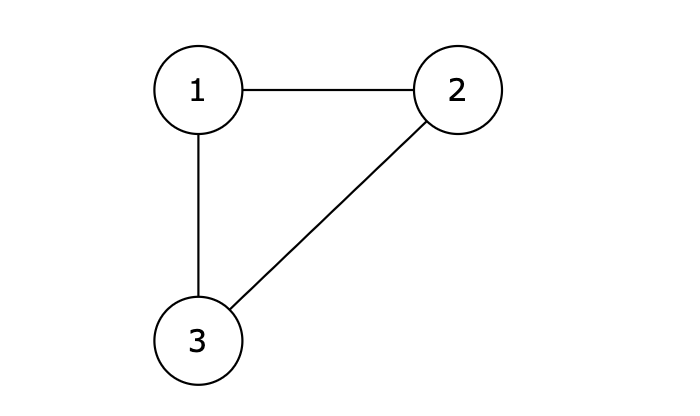
图中的 1 2，2 3，1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输出里最后出现的那条边，所以输出结果为 1 3

数据范围：

1 <= N <= 1000.

#include <iostream>
#include <vector>
using namespace std;int n;
vector<int> father(1001,0);void init()
{for(int i=1;i<=n;i++)father[i]=i;
}int find(int u)
{return u==father[u]?u:father[u]=find(father[u]);
}bool isSame(int u,int v)
{u=find(u);v=find(v);return u==v;
}void join(int u,int v)
{u=find(u);v=find(v);if(u==v)return;elsefather[v]=u;
}int main()
{cin>>n;init();int s,t;for(int i=0;i<n;i++){cin>>s>>t;if(isSame(s,t)){cout<<s<<" "<<t<<endl;return 0;}elsejoin(s,t);}
}

109.冗余连接II（卡码网）【并查集 摧毁信心的一题，胆小的走开！】

题目描述

有一种有向树,该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。有向树拥有 n 个节点和 n - 1 条边。如图：

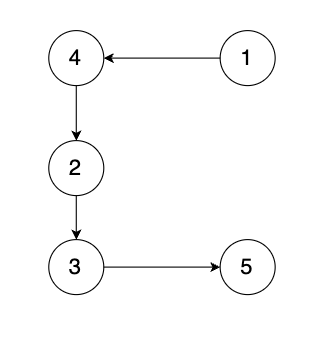
现在有一个有向图，有向图是在有向树中的两个没有直接链接的节点中间添加一条有向边。如图：

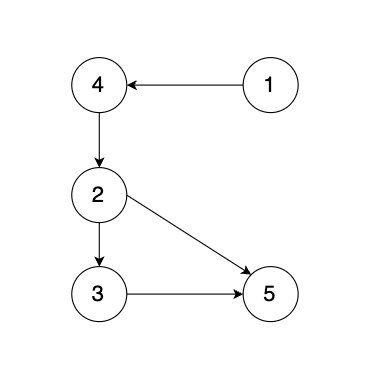
输入一个有向图，该图由一个有着 n 个节点(节点编号 从 1 到 n)，n 条边，请返回一条可以删除的边，使得删除该条边之后该有向图可以被当作一颗有向树。

输入描述

第一行输入一个整数 N，表示有向图中节点和边的个数。

后续 N 行，每行输入两个整数 s 和 t，代表这是 s 节点连接并指向 t 节点的单向边

输出描述

输出一条可以删除的边，若有多条边可以删除，请输出标准输入中最后出现的一条边。

输入示例

3
1 2
1 3
2 3

输出示例

2 3

提示信息

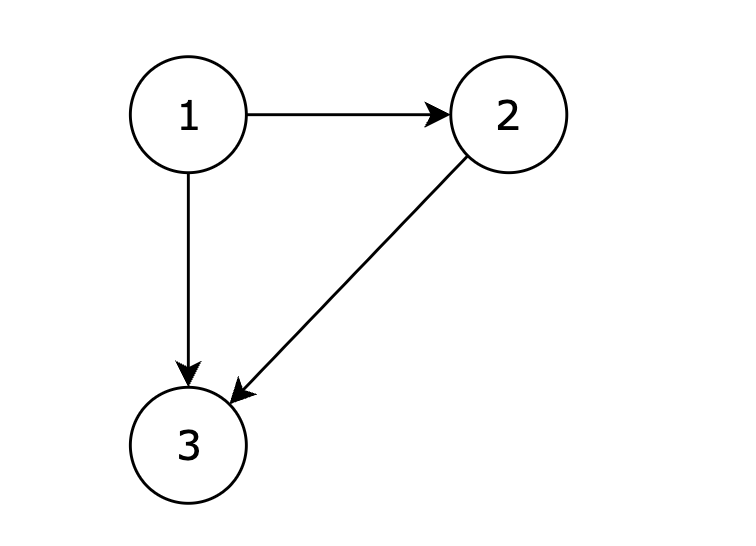
在删除 2 3 后有向图可以变为一棵合法的有向树，所以输出 2 3

数据范围：

1 <= N <= 1000.

#include <iostream>
#include <vector>
using namespace std;int n;
vector<int> father(1001,0);void init()
{for(int i=1;i<=n;i++)father[i]=i;
}int find(int u)
{return u==father[u]?u:father[u]=find(father[u]);
}bool isSame(int u,int v)
{u=find(u);v=find(v);return u==v;
}void join(int u,int v)
{u=find(u);v=find(v);if(u==v)return;elsefather[v]=u;
}bool deleteIsTree(vector<vector<int>> edges,int x)
{init();for(int i=0;i<n;i++){if(i==x) continue;if(isSame(edges[i][0],edges[i][1]))return false;elsejoin(edges[i][0],edges[i][1]);}return true;
}void removeEdge(vector<vector<int>> edges)
{init();for(int i=0;i<n;i++){if(isSame(edges[i][0],edges[i][1]))cout<<edges[i][0]<<" "<<edges[i][1]<<endl;elsejoin(edges[i][0],edges[i][1]);}
}int main()
{int s,t;cin>>n;vector<vector<int>> edges;vector<int> inDegree(n+1,0);vector<int> vec;for(int i=0;i<n;i++){cin>>s>>t;edges.push_back({s,t});inDegree[t]++;}for(int i=n-1;i>0;i--){if(inDegree[edges[i][1]]==2)vec.push_back(i);}if(vec.size()>0){if(deleteIsTree(edges,vec[0]))cout<<edges[vec[0]][0]<<" "<<edges[vec[0]][1]<<endl;elsecout<<edges[vec[1]][0]<<" "<<edges[vec[1]][1]<<endl;return 0;}removeEdge(edges);
}