生成 Excel 表列名称
Excel 大家都用过,它的列名是用字母编号的,A 表示第一列,B 表示第二列,AA 表示第27列,AB 表示第28列等等。
现给定一个数字,如何得到列名称呢。比如输入28,输出 AB。
一开始以为就是一个简单的26进制转换,到底还是大意了,这里的每一位都是没有0的,而且能取到进制的最大值。正常26进制每一位都是0到25,但是这里却是1到26。
算法原理还是不停的取模和取余来得到每一位的值。只不过和正常的 n 进制转换不同,我们不能直接用 n 去取模和取余,而是应该用 n-1。
还是按26进制计算,假设要表示的数为 num,余数为 r,则:
n u m = n × 26 + r num = n \times 26+r num=n×26+r
其中 r r r 的范围是0到25,假设 R R R 的范围是1到26,我们将 r r r 线性映射到 R R R,并将 r r r 替换成 R R R,于是:
n × 26 + R = n u m + 1 n \times 26+R=num+1 n×26+R=num+1
我们会发现在将 r r r 替换成 R R R 的过程中, n u m num num 实际上每次都多加了1,所以在计算每一位的值时要将它减出来。
另外我们可以想一下,在取余的过程中,有两种情况:
n u m = n × 26 + r n u m = n × 26 \begin{align} num & = n \times 26 + r \\ num & = n \times 26 \end{align} numnum=n×26+r=n×26
第一种情况其实可以正常计算,第二中情况不行,因为不会出现0,所以我们需要改写一下:
n u m = ( n − 1 ) × 26 + 26 num=(n-1)\times 26 + 26 num=(n−1)×26+26
但是正常取余运算算不出这个余数,怎么办呢,给 n u m num num 减去1就可以了:
n u m − 1 = ( n − 1 ) × 26 + 25 num-1=(n-1)\times 26 + 25 num−1=(n−1)×26+25
对于其他情况也一样,于是就统一变成了:
n u m − 1 = n × 26 + ( r − 1 ) num-1=n \times 26 + (r-1) num−1=n×26+(r−1)
至于多减的1,会自动补回来。
defmodule Solution do@spec convert_to_title(column_number :: integer) :: String.tdef convert_to_title(column_number) do{column_number, 26}|> Stream.unfold(fn{0, _} -> nil{n, m} -> {rem(n - 1, m) + ?A, {div(n - 1, m), m}} end)|> Enum.reverse|> List.to_stringend
end
在 Elixir 中,我们可以通过 Stream.unfold 来构造每一位的值,连递归都不用写了,可以说是十分优雅了。

相关文章:

生成 Excel 表列名称
Excel 大家都用过,它的列名是用字母编号的,A 表示第一列,B 表示第二列,AA 表示第27列,AB 表示第28列等等。 现给定一个数字,如何得到列名称呢。比如输入28,输出 AB。 一开始以为就是一个简单的…...

基于yolov10的烟雾明火检测森林火灾系统python源码+pytorch模型+评估指标曲线+精美GUI界面+数据集
【算法介绍】 基于YOLOv10的烟雾明火检测森林火灾系统是一种先进的火灾预警系统,它结合了深度学习和计算机视觉技术,能够实时检测和分析森林中的烟雾和明火,从而有效预防和控制森林火灾的发生。 该系统主要基于YOLOv10模型进行构建…...

UltraISO(软碟通)制作U盘制作Ubuntu20.04启动盘
目录 一、启动盘制作 1、工具准备 2、打开UltraISO后,点击左上角的文件,在打开的下拉项中,选择打开准备好的Ubuntu系统20.04 LTS镜像文件(ubuntu-20.04-desktop-amd64.iso); 3、然后点击启动->写入硬盘映像 4、在弹出的窗…...

【EtherCAT实践篇一】TwinCAT 3安装、使用
TwinCAT 基于 PC 的开放式控制技术 倍福推出的基于 PC 的控制技术定义了自动化领域的全球标准。在软件方面,1996 年推出的 TwinCAT(The Windows Control and Automation Technology,基于 Windows 的控制和自动化技术)自动化套件是…...
4、CSS3笔记
文章目录 四、CSS3CSS3简介css3概述CSS3私有前缀什么是私有前缀为什么要有私有前缀常见浏览器私有前缀 CSS3基本语法CSS3新增长度单位CSS3新增颜色设置方式CSS3新增选择器CSS3新增盒模型相关属性box-sizing 怪异盒模型resize 调整盒子大小box-shadow 盒子阴影opacity 不透明度 …...

Docker无法拉取镜像解决办法
Docker 无法拉取镜像解决办法 一.现象描述 在docker拉取镜像的时候重复拉取镜像然后超时。 二.解决办法 1.配置国内镜像源地址加速 vi /etc/docker/daemon.json在文件中增加如下内容 { "registry-mirrors": ["https://docker.m.daocloud.io","h…...

Ubuntu 20.04安装Qt 5.15(最新,超详细)
Ubuntu 20.04安装Qt 5.15 1. 准备注册Qt账号安装依赖下载安装工具 2. 安装3. 测试参考 前言 Qt 是一个跨平台的应用程序框架,它支持开发 C 图形用户界面应用程序。Qt 可以用于开发运行在多种操作系统上的应用程序,包括 Windows、Linux、macOS 和各种移动…...

桂林旅游一点通:SpringBoot平台应用
3系统分析 3.1可行性分析 通过对本桂林旅游景点导游平台实行的目的初步调查和分析,提出可行性方案并对其一一进行论证。我们在这里主要从技术可行性、经济可行性、操作可行性等方面进行分析。 3.1.1技术可行性 本桂林旅游景点导游平台采用SSM框架,JAVA作…...

【WPF】04 Http消息处理类
这里引入微软官方提供的HttpClient类来实现我们的目的。 首先,介绍一下官方HttpClient类的内容。 HttpClient 类 定义 命名空间: System.Net.Http 程序集: System.Net.Http.dll Source: HttpClient.cs 提供一个类,用于从 URI 标识的资源发送 HTTP 请…...

如何精准设置线程数,提升系统性能的秘密武器!
线程数设定多少更合适? 线程数的设定需要根据任务的类型、系统资源、以及并发需求来进行权衡。设定合适的线程数可以有效提升系统的性能,但设置过多或过少都会影响程序的效率。以下是一些关键因素和计算方法,用于帮助确定最合适的线程数。 …...

正则表达式:从入门到精通
正则表达式(Regular Expression,简称 regex)是一种强大的文本匹配和处理工具。它可以用于搜索、替换、验证和提取文本中的特定模式。本文将带您深入了解正则表达式的各个方面,从基础知识到高级技巧。 1. 基础知识 1.1 什么是正则表达式? 正则表达式是由一系列字符和特殊…...
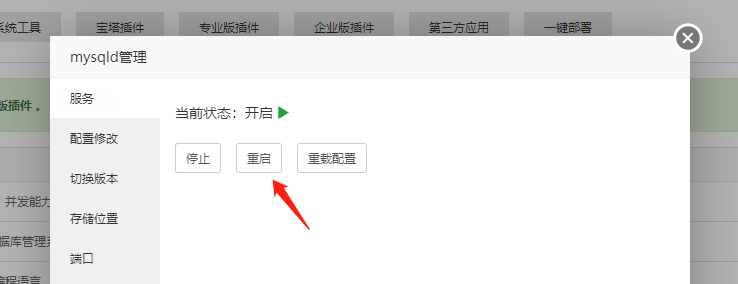
CRMEB标准版Mysql修改sql_mode
数据库配置 1.宝塔控制面板-软件商店-MySql-设置 2.点击配置修改,查找sql-mode或sql_mode (可使用CtrlF快捷查找) 3.复制 NO_AUTO_CREATE_USER,NO_ENGINE_SUBSTITUTION 然后替换粘贴,保存 注:MySQL8.0版本的 第三步用…...
linux驱动访问的地址为虚拟地址
在Linux驱动程序中,访问的内存地址通常是虚拟地址。这是因为Linux操作系统采用了虚拟内存管理机制,所有的用户空间和内核空间的内存地址都是虚拟地址。下面是一些关键点,以帮助更好地理解这个概念: 虚拟地址与物理地址࿱…...
基于SpringBoot+Vue+uniapp微信小程序的社区门诊管理系统的详细设计和实现(源码+lw+部署文档+讲解等)
项目运行截图 技术框架 后端采用SpringBoot框架 Spring Boot 是一个用于快速开发基于 Spring 框架的应用程序的开源框架。它采用约定大于配置的理念,提供了一套默认的配置,让开发者可以更专注于业务逻辑而不是配置文件。Spring Boot 通过自动化配置和约…...

使用WPF写一个简单的开关控件
<Window x:Class"WPF练习.MainWindow"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d"http://schemas.microsoft.com/expression/blend/2008"xm…...

FPGA采集adc,IP核用法,AD驱动(上半部分)
未完结,明天补全 IP核:集成的一个现有的模块 串口写好后基本不会再修改串口模块内部的一些逻辑,将串口.v文件添加进来,之后通过他的上层的接口去对他进行使用,所以我们打包IP,之后就不用去添加源文件了&a…...

MongoDB 如何做mapreduce
以下是在MongoDB中使用MapReduce的详细步骤和相关说明: 1. MapReduce的概念 MapReduce是一种用于大规模数据处理的编程模型,它由两个主要阶段组成:Map阶段和Reduce阶段。在MongoDB中,MapReduce操作允许在服务器端对数据进行批量…...

Vue是一套构建用户界面的渐进式框架,常用于构建单页面应用
学习总结 1、掌握 JAVA入门到进阶知识(持续写作中……) 2、学会Oracle数据库入门到入土用法(创作中……) 3、手把手教你开发炫酷的vbs脚本制作(完善中……) 4、牛逼哄哄的 IDEA编程利器技巧(编写中……) 5、面经吐血整理的 面试技…...

c++ 桶排序(看这一篇就够了)
1. 概述 桶排序(Bucket Sort)又称箱排序,是一种比较常用的排序算法。其算法原理是将数组分到有限数量的桶里,再对每个桶分别排好序(可以是递归使用桶排序,也可以是使用其他排序算法将每个桶分别排好序&…...
格点拉格朗日插值与PME算法
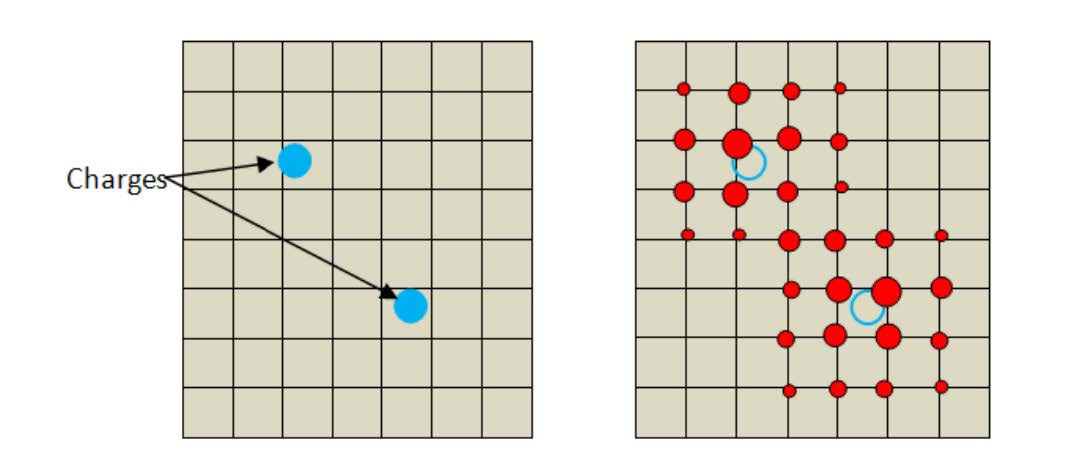
技术背景 在前面的一篇博客中,我们介绍了拉格朗日插值法的基本由来和表示形式。这里我们要介绍一种拉格朗日插值法的应用场景:格点拉格朗日插值法。这种场景的优势在于,如果我们要对整个实数空间进行求和或者积分,计算量是随着变量…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
