【人工智能-初级】第2章 机器学习入门:从线性回归开始
文章目录
- 一、什么是线性回归?
- 二、线性回归的基本概念
- 2.1 一元线性回归
- 2.2 多元线性回归
- 三、如何进行线性回归建模?
- 四、用Python实现线性回归
- 4.1 导入必要的库
- 4.2 创建虚拟数据集
- 4.3 数据可视化
- 4.4 拆分训练集和测试集
- 4.5 训练线性回归模型
- 4.6 查看模型的参数
- 4.7 模型预测与评估
- 4.8 可视化拟合效果
- 五、总结
- 5.1 学习要点
- 5.2 练习题
一、什么是线性回归?
线性回归(Linear Regression)是机器学习中最基础的算法之一,它主要用于解决回归问题。简单来说,线性回归就是找到一个合适的直线来描述数据之间的关系,并用这个直线进行预测。
在生活中,我们常常会遇到这样的场景:你想知道房子的面积和价格之间的关系,或者想了解广告投放和产品销售之间的联系。这些情况中,存在一种变量随着另一种变量而变化的趋势,这就是线性关系。而线性回归模型的目的就是找到这个趋势,用一个数学公式将这种线性关系表示出来。
二、线性回归的基本概念
线性回归的目标是找到一个函数,它能够尽可能准确地预测输入变量(通常叫做自变量)和输出变量(通常叫做因变量)之间的关系。这个函数通常是一个线性方程,其形式为:
y = w x + b y = w x + b y=wx+b
- y:预测值或因变量。
- x:输入特征或自变量。
- w:模型的权重或斜率。
- b:偏置项,也叫截距,它表示直线在y轴上的截距。
通过调整 w 和 b 的值,我们可以让这条直线尽可能“拟合”数据,使得我们的预测值与真实值之间的误差尽可能小。
2.1 一元线性回归
最简单的线性回归是一元线性回归,它只有一个自变量,即用一个特征预测一个输出值。例如,用房子的面积预测房子的价格。
y = w x + b y = w x + b y=wx+b
在这个公式中,w 是描述房价随面积变化的速率,b 是当面积为0时的房价(当然这种情况在现实中并没有实际意义,但它是数学上的一个假设)。
2.2 多元线性回归
当有多个自变量时,线性回归就变成了多元线性回归。例如,我们用房子的面积、房间数量和建筑年份来预测房价,这时公式变为:
y = w 1 x 1 + w 2 x 2 + w 3 x 3 + . . . + b y = w_1 x_1 + w_2 x_2 + w_3 x_3 + ... + b y=w1x1+w2x2+w3x3+...+b
其中,w1, w2, w3 分别表示每个特征的权重,x1, x2, x3 是各个特征值,b 依旧是截距。
三、如何进行线性回归建模?
线性回归的建模过程包括以下几个步骤:
- 数据收集和准备:收集数据,并对数据进行清洗和预处理。
- 数据可视化:使用图表等手段查看数据,以确定变量之间是否存在线性关系。
- 模型训练:使用线性回归算法拟合模型,找出最优的 w 和 b。
- 模型评估:通过评价指标来衡量模型的好坏,例如均方误差(MSE)。
- 模型预测:使用训练好的模型对新数据进行预测。
四、用Python实现线性回归
下面我们将通过Python来实现一个简单的一元线性回归模型,使用一个虚拟的数据集来说明整个过程。
4.1 导入必要的库
首先,我们需要导入一些库,这些库将帮助我们完成数据分析和建模工作。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
- numpy:用于进行数值计算。
- matplotlib:用于绘制数据可视化图表。
- sklearn:一个流行的机器学习库,包含许多常用的机器学习算法和工具。
4.2 创建虚拟数据集
我们创建一个简单的数据集,其中包含自变量 x 和因变量 y,并且两者之间存在线性关系。
# 生成随机数据
np.random.seed(0)
x = 2 * np.random.rand(100, 1)
y = 4 + 3 * x + np.random.randn(100, 1)
- np.random.seed(0):设置随机数种子,使得每次生成的随机数相同,方便实验复现。
- x:自变量,随机生成的100个数,每个数介于0到2之间。
- y:因变量,根据线性方程生成,加上了一些噪声(np.random.randn),以模拟实际中的数据。
4.3 数据可视化
绘制数据散点图,以便观察自变量和因变量之间是否存在线性关系。
plt.scatter(x, y, color='blue')
plt.xlabel("x")
plt.ylabel("y")
plt.title("Scatter Plot of Dataset")
plt.show()
运行上述代码后,我们将看到一个散点图,这些点大致呈现线性分布,说明可以用线性回归模型来拟合。
4.4 拆分训练集和测试集
在进行建模之前,我们将数据集拆分为训练集和测试集,以便评估模型的表现。
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42)
- train_test_split:将数据随机分为训练集和测试集,test_size=0.2 表示20%的数据用于测试,80%用于训练。
4.5 训练线性回归模型
使用 scikit-learn 提供的 LinearRegression 类来拟合模型。
model = LinearRegression()
model.fit(x_train, y_train)
- model.fit(x_train, y_train):使用训练集数据来训练线性回归模型。训练的过程就是找到最佳的 w 和 b。
4.6 查看模型的参数
训练完成后,我们可以查看模型学习到的权重和截距。
w = model.coef_[0][0]
b = model.intercept_[0]
print(f"模型的权重 w: {w}")
print(f"模型的截距 b: {b}")
这些参数就是拟合出来的直线的方程:
y = w ∗ x + b y = w * x + b y=w∗x+b
4.7 模型预测与评估
使用测试集对模型进行评估,并计算模型的均方误差(MSE)。
y_pred = model.predict(x_test)# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print(f"均方误差 MSE: {mse}")
- mean_squared_error:计算预测值和真实值之间的平均平方误差,误差越小,说明模型的拟合效果越好。
4.8 可视化拟合效果
最后,我们可以将拟合的直线绘制在散点图上,直观地看到模型的拟合效果。
plt.scatter(x, y, color='blue', label='Data')
plt.plot(x, model.predict(x), color='red', linewidth=2, label='Linear Fit')
plt.xlabel("x")
plt.ylabel("y")
plt.title("Linear Regression Fit")
plt.legend()
plt.show()
在图中,蓝色的散点是我们的原始数据,红色的直线是模型拟合出来的直线。可以看到这条直线很好地描述了数据之间的关系。
五、总结
线性回归是机器学习中最基础的算法之一,适用于那些变量之间存在线性关系的问题。通过本文的介绍,我们了解了线性回归的基本概念、数学公式以及如何用Python进行建模。掌握线性回归对于理解更复杂的机器学习和深度学习算法有很大的帮助。
5.1 学习要点
- 线性回归的基本形式是 y = wx + b,其中 w 是权重,b 是截距。
- 一元线性回归用于一个特征的情况,而多元线性回归用于多个特征的情况。
- 使用Python库(如 scikit-learn)可以很方便地实现线性回归模型。
- 训练模型时需要将数据集拆分为训练集和测试集,以便评估模型的泛化能力。
5.2 练习题
- 在本例中的数据上,尝试增加更多的噪声,观察模型的拟合效果会发生怎样的变化?
- 使用多元线性回归,尝试预测一个虚拟的房价数据集。
- 使用 sklearn.datasets 模块中的 load_boston 数据集,构建一个线性回归模型,预测房屋价格。
这篇文章介绍的线性回归仅仅是机器学习的一个起点,希望大家通过动手实践能够对其有更加深刻的理解。如果有任何问题,欢迎在评论中讨论!
如果您觉得本文有帮助,欢迎继续学习本专栏的其他内容,下一篇文章将为您介绍K-最近邻(KNN)算法及其Python实现。
相关文章:

【人工智能-初级】第2章 机器学习入门:从线性回归开始
文章目录 一、什么是线性回归?二、线性回归的基本概念2.1 一元线性回归2.2 多元线性回归 三、如何进行线性回归建模?四、用Python实现线性回归4.1 导入必要的库4.2 创建虚拟数据集4.3 数据可视化4.4 拆分训练集和测试集4.5 训练线性回归模型4.6 查看模型…...

SPOOLing技术详解,结合实际场景让你了解什么是假脱机技术。
SPOOLing技术 在手工操作阶段,主机直接从I/O设备获取数据,但是由于设备速度很慢,主机速度很快。人机速度矛盾明显,主机需要浪费很多时间来等待设备。 什么是脱机技术,脱机技术可以解决什么问题? 所谓脱…...

基于SSM汽车零部件加工系统的设计
管理员账户功能包括:系统首页,个人中心,员工管理,经理管理,零件材料管理,产品类型管理,产品信息管理,产品出库管理,产品入库管理 员工账号功能包括:系统首页…...

改进 JavaScript 条件语句,探索可以替代 if...else 的 7 种方式!
当优化 JavaScript 代码时,条件语句是一个经常需要思考和改进的关键部分。if...else 结构虽然是我们常用的条件语句之一,但当代码逻辑变得复杂,if...else 结构可能会导致代码冗长、难以维护和理解。因此,了解并掌握优化 if...else…...

全新子比主题7.9.2开心版 子比主题最新版源码
内容目录 一、详细介绍二、效果展示1.部分代码2.效果图展示 三、学习资料下载 一、详细介绍 wordpress zibll子比主题7.9.2开心版 修复评论弹授权 可做付费下载站 含wordpress搭建视频教程zibll子比主题安装视频教程支付配置视频教程,视频都是语音讲解,…...

Kafka之消费者组与消费者
消费者(Consumer)在Kafka的体系结构中是用来负责订阅Kafka中的主题(Topic),并从订阅的主题中拉取消息后进行处理。 与其他消息中间件不同,Kafka引入一个逻辑概念——消费组(Consumer Group&…...
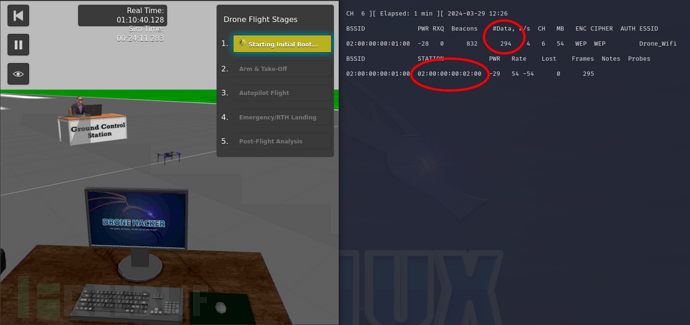
Damn-Vulnerable-Drone:一款针对无人机安全研究与分析的靶机工具
关于Damn-Vulnerable-Drone Damn-Vulnerable-Drone是一款针对无人机安全研究与分析的靶机工具,广大研究人员可以利用该环境工具轻松学习、研究和分析针对无人机安全态势。 Damn Vulnerable Drone 基于流行的 ArduPilot/MAVLink 架构,其中故意留下了各种…...

项目模块三:Socket模块
一、模块设计 1、套接字编程常用头文件展示 #include <sys/types.h> #include <sys/socket.h> #include <netinet/in.h> #include <arpa/inet.h> #include <unistd.h> #include <fcntl.h> 2、成员函数设计 (1…...

Unity-Shader-语义
1、从程序传给顶点函数: POSITION:顶点坐标(模型空间下) NORMAL:法线向量(模型空间下) TANGENT:切线向量(模型空间下) TEXCOORD0~n:纹理坐标 …...

MFC工控项目实例二十四模拟量校正值输入
承接专栏《MFC工控项目实例二十三模拟量输入设置界面》 对模拟量输入的零点校正值及满量程对应的电压值进行输入。 1、在SenSet.h文件中添加代码 #include "BtnST.h" #include "ShadeButtonST.h"/ // SenSet dialogclass SenSet : public CDialog { // Co…...

analysis-ik分词器
analysis-ik分词器 1、安装离线在线 2、使用配置拓展词典 3、测试ik_smartik_max_word 1、安装 离线 使用离线安装下载地址https://release.infinilabs.com/analysis-ik/stable/找到对应es版本的ik分词器、下载zip后放到/elasticsearch/plugins/ik文件夹下。重启es即可生效 …...

开源的、基于内存的键值存储数据库redis详细介绍
目录 一、Redis的概述 1、概述 2、特点 (1)基本特性 (2)数据结构 (3)运行环境 二、Redis的重要作用 1、缓存 2、会话存储 3、消息队列 4、计数器 5、分布式锁 6、排行榜 7、实时数据处理 三、…...

三种容器 std::vector、std::map、std::unordered_set 的对比分析
目录 1.添加元素 1.1 std::vector 1.2 std::map 1.3 std::unordered_set 2. 查找元素 2.1 std::vector 2.2 std::map 2.3 std::unordered_set 3. 遍历容器 3.1 std::vector 使用范围基for循环(range-based for loop) 使用迭代器: 3.2 std::map 3.3 std::unord…...

Nuxt3 SSR 服务端渲染部署 PM2 全流程(Nest.js 同理)
项目打包 我们以 Nuxt3 项目为例子: 项目打包 执行 npm run build , 生成的 .output 文件夹就是部署产物(目前不支持中文路径)执行 npm run preview 可以本地预览效果 方式一:使用 Node 部署 需要服务器安装 Nod…...

如何轻松使用pip安装Git仓库中的私有Python模块(使用pip和Git仓库发布和安装私有Python模块)
文章目录 📖 介绍 📖🏡 演示环境 🏡📒 Git模块 📒📝 Git仓库要求🔖 项目目录结构🔖 文件说明📝 编写setup.py📝 配置MANIFEST.in📝 推送代码到Git仓库📝 使用pip安装模块🔖 使用用户名和密码🔖 使用Personal Access Token (PAT)🔖 示例📝 更…...

写 R 包教程
R R 包开发 | 保姆级教程-CSDN博客 https://www.prestevez.com/post/r-package-tutorial/ 1、加载开发所需 R 包 library(usethis) library(devtools) library(roxygen2) 2、在当前工作路径创建 R 包 usethis::create_package("myRpkg") # 在当前路径创建 my…...
【java】数组(超详细总结)
目录 一.一维数组的定义 1.创建数组 2.初始化数组 二.数组的使用 1.访问数组 2.遍历数组 3.修改数据内容 三.有关数组方法的使用 1.toString 2. copyOf 四.查找数组中的元素 1.顺序查找 2.二分查找binarySearch 五.数组排序 1.冒泡排序 2.排序方法sort 六.数组逆置…...

@KafkaListener注解
KafkaListener(topics "${xxxx}", containerFactory "xxx") public void consume(String message) {service.save(xx); }在 Spring Boot 中,使用 KafkaListener 注解消费 Kafka 消息时,如果 service.save(cleanWikiSource) 抛出异…...

2025年计算机视觉研究进展与应用国际学术会议 (ACVRA 2025)
2025年计算机视觉研究进展与应用国际学术会议 (ACVRA 2025) 2025 International Conference on Advances in Computer Vision Research and Applications 重要信息 2025年3月28-30日 南京 一轮截稿日期:2024年11月30日 EI检索稳定 早投稿,早审稿&a…...

第二代GPT-SoVITS V2:让声音克隆变得简单
随着人工智能技术的飞速发展,AI声音克隆已经成为一种趋势,广泛应用于各个领域。为了满足更多用户的需求,第二代GPT-SoVITS V2应运而生,它由RVC变声器创始人“花儿不哭”与AI音色转换技术Sovits开发者Rcell联合开发,是一…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
