UEFI EDK2框架学习 (四)——UEFI图形化
一、修改protocol.c
#include <Uefi.h>
#include <Library/UefiLib.h>
#include <Library/UefiBootServicesTableLib.h>
#include <stdio.h>EFI_STATUS
EFIAPI
UefiMain(IN EFI_HANDLE ImageHandle,IN EFI_SYSTEM_TABLE *SystemTable
) {EFI_STATUS Status = EFI_SUCCESS;UINTN NoHandles = 0;EFI_HANDLE *Buffer = NULL;Status = gBS->LocateHandleBuffer(ByProtocol,&gEfiGraphicsOutputProtocolGuid,NULL,&NoHandles,&Buffer);Print(L"Status = %d", Status);if (EFI_ERROR(Status)) {Print(L"Failed to LocateHandleBuffer. \n");return Status;}Print(L"Hello, Protocol\n");EFI_GRAPHICS_OUTPUT_PROTOCOL *Gop;Status = gBS->OpenProtocol(Buffer[0],&gEfiGraphicsOutputProtocolGuid,(VOID**)&Gop,ImageHandle,NULL,EFI_OPEN_PROTOCOL_GET_PROTOCOL);Print(L"Status = %d", Status);if (EFI_ERROR(Status)) {Print(L"Failed to OpenProtocol. \n");return Status;}UINTN SizeOfInfo = 0;EFI_GRAPHICS_OUTPUT_MODE_INFORMATION *Info;UINTN i = 0;for (; i < Gop->Mode->MaxMode; i++) {Status = Gop->QueryMode(Gop, i, &SizeOfInfo, &Info);if (EFI_ERROR(Status)) {Print(L"Failed to Querymode. \n");return Status;}PrintL(L"Mode %d, H = %d, V = %d", i, Info->HorizontalResolution, Info->VerticalResolution);}Status = Gop->SetMode(Gop, 22);if (EFI_ERROR(Status)) {Print(L"Failed to Querymode. \n");return Status;}EFI_GRAPHICS_OUTPUT_BLT_PIXEL Red = {0, 0, 255, 0};Gop->Blt(Gop,&Red,EfiBltVideoFill,0,0, // source x y0,0,100,100, // wid height0);if (EFI_ERROR(Status)) {Print(L"Failed to Blt. \n");return Status;}Gop->Blt(Gop,&Red,EfiBltVideoFill,0,0, // source x y200, 200,100,100, // wid height0); // copyif (EFI_ERROR(Status)) {Print(L"Failed to Blt. \n");return Status;}return Status;
}
二、build

相关文章:

UEFI EDK2框架学习 (四)——UEFI图形化
一、修改protocol.c #include <Uefi.h> #include <Library/UefiLib.h> #include <Library/UefiBootServicesTableLib.h> #include <stdio.h>EFI_STATUS EFIAPI UefiMain(IN EFI_HANDLE ImageHandle,IN EFI_SYSTEM_TABLE *SystemTable ) {EFI_STATUS S…...

【C++】— 一篇文章让你认识STL
文章目录 🌵1.什么是STL?🌵2.STL的版本🌵3.STL的六大组件🌵4.STL的重要性🌵5. 如何学习STL🌵6. 学习STL的三种境界 🌵1.什么是STL? STL是Standard Template Library的简称…...

mysql--索引
目录 1、长什么样 2、硬件理解 3、软件理解 4、进一步认识 5、索引的理解 6、为什么不选择其他数据结果? 7、聚簇索引和非聚簇索引 8、索引操作 (1)主键索引创建 第一种方式 第二种方式 第三种方式 主键索引的特点 (…...
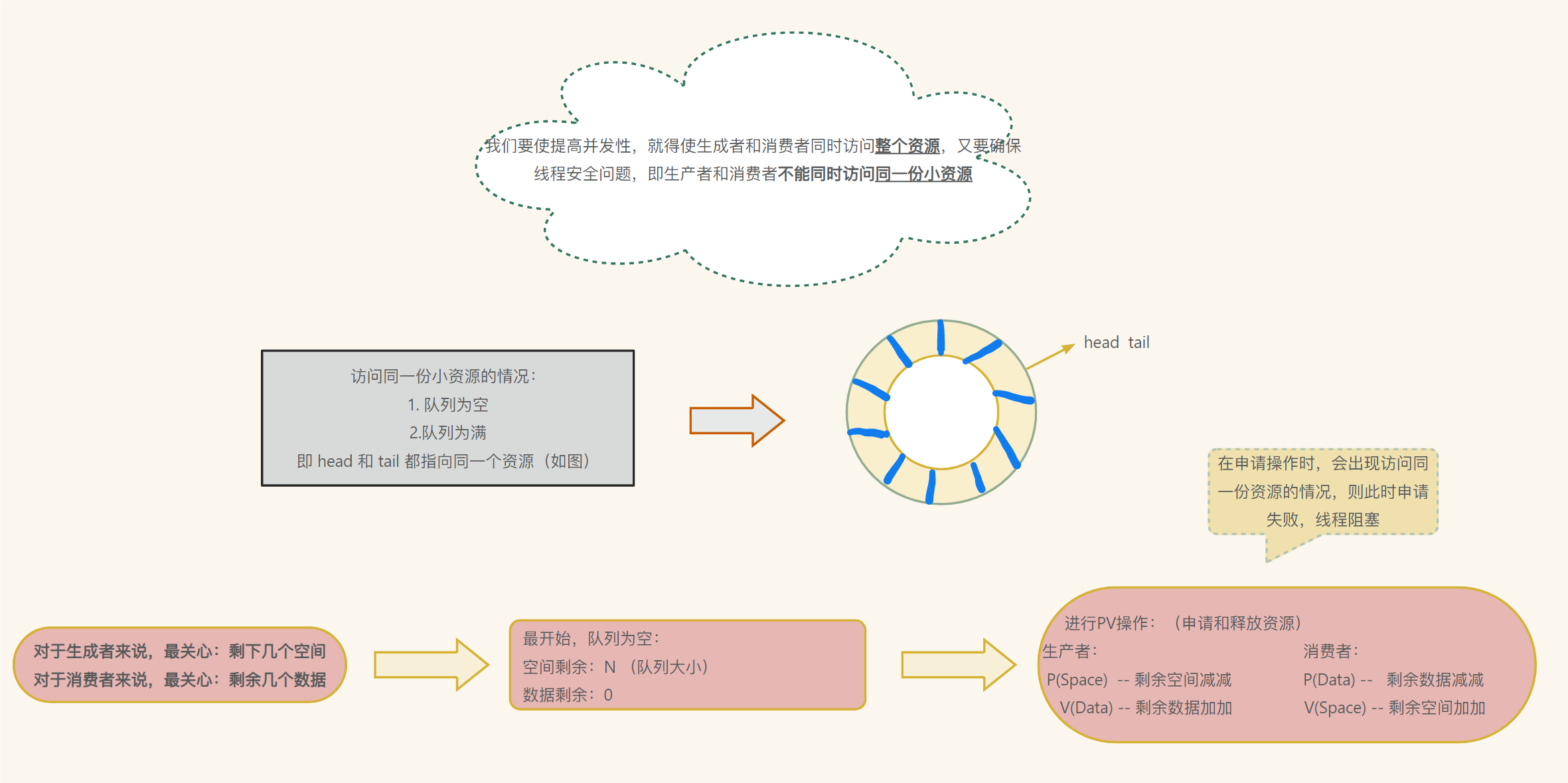
【linux】线程 (三)
13. 常见锁概念 (一)了解死锁 死锁是指在一组进程中的各个进程均占有不会释放的资源,但因互相申请被其他进程占有的,且不释放的资源,而处于的一种永久等待状态 (二)死锁四个必要条件 互斥条件…...

c++日常积累
在 C 中,可以直接将 int 类型的值赋值给 bool 类型。C 会自动进行类型转换,任何非零的 int 值都会被转换为 true,而 0 会被转换为 false。 QDialog 有一个 finished(int) 信号,该信号在对话框关闭时发出,并传递一个整…...

字节流写入文件
一、创建输出流对象表示的文件三种方式 方法一: FileOutputStream fos new FileOutputStream("fos.txt",true);//最简便方法二: FileOutputStream fos new FileOutputStream(new File("fos.txt"));方法三; File f ne…...

Torch模型导入
冻结param的3种方式 for param in net.lstm.parameters():param.requires_grad Truenet.lstm.requires_grad True # 无效net.lstm.state_dict()[weight_ih_l0].requires_gradFalsenet.lstm.weight_ih_l0.requires_grad False# dir(net.lstm) to validate attributes …...

博弈论:博弈类型空间集合;三层博弈拓展式;
目录 博弈论:博弈类型空间集合 θ(Dss-1=1 )就是博弈类型空间集合; 一、博弈的基本要素 二、博弈的主要类型 三、博弈类型空间集合的构建 三层博弈拓展式: 博弈论:博弈类型空间集合 这的博弈类型空间集合:指一方选择的策略,用符号进行表达:SDss-2(θDss-1=1) = …...

数据库表的关联、集合操作
数据库表的关联、集合操作 join、MySQL、Oracle什么left right的老是忘,归根到底还是不熟练,记录下来,以后就不用再搜了。 设表A、表B分别包含员工信息和部门信息。 表A包含员工的ID、姓名和部门ID, 表B包含部门ID和部门名称。 …...
word怎么清除格式,Word一键清除所有格式教程
你是否曾在编辑Word文档时遇到过复制内容时格式混乱的情况?别担心,这只需要清除一下格式就可以了,很多朋友还不知道word怎么清除格式,下面小编就来给大家讲一讲word一键清除所有格式的方法教程,操作非常简单,有需要的…...

ShardingProxy服务端分库分表
目录 一、为什么要有服务端分库分表? 二、ShardingProxy基础使用 1、部署ShardingProxy 2、配置常用分库分表策略 三、ShardingSphere中的分布式事务机制 1、什么是XA事务? 2、实战理解XA事务 3、如何在ShardingProxy中使用另外两种事务管理器&a…...
 项目)
开源的 FOC(Field-Oriented Control) 项目
开源的 FOC(Field-Oriented Control) 项目通常用于控制无刷直流电机(BLDC)和永磁同步电机(PMSM)。这些项目可以实现高效的电机控制,广泛应用于机器人、无人机、电动车等领域。以下是一些著名的开…...

高等数学 5.5 反常积分的审敛法 Γ函数
文章目录 一、无穷限反常积分的审敛法二、无界函数的反常积分审敛法三、 Γ \Gamma Γ 函数 一、无穷限反常积分的审敛法 定理1 设函数 f ( x ) f(x) f(x) 在区间 [ a , ∞ ) [a, \infty) [a,∞) 上连续,且 f ( x ) ⩾ 0 f(x) \geqslant 0 f(x)⩾0.若函数 F (…...

宝塔安装ffmpeg的方法
宝塔安装ffmpeg的方法 wget http://download.bt.cn/install/ext/ffmpeg.sh && sh ffmpeg.sh安装完后可输入以下命令是否安装成功: ffmpeg -version...
案例分享-优秀蓝色系UI界面赏析
蓝色UI设计界面要提升舒适度,关键在于色彩搭配与对比度。选择柔和的蓝色调作为主色,搭配浅灰或白色作为辅助色,能营造清新、宁静的氛围。同时,确保文字与背景之间有足够的对比度,避免视觉疲劳,提升阅读体验…...

陪诊小程序之uniapp(从入门到精通)
1.uniapp如何使用vue3编写页面 <template><view class"content"><navbar name"navbar组件"></navbar><image class"logo" src"/static/logo.png"></image><view class"text-area"&…...

深度学习(一)基础:神经网络、训练过程与激活函数(1/10)
深度学习基础:神经网络、训练过程与激活函数 引言: 深度学习作为机器学习的一个子领域,近年来在人工智能的发展中扮演了举足轻重的角色。它通过模仿人脑的神经网络结构,使得计算机能够从数据中学习复杂的模式和特征,…...

源代码加密技术的一大新方向!
在当今这个信息爆炸的时代,企业所面临的数据安全挑战日益严峻。传统的文档加密方法已经无法满足日益复杂的安全需求。幸运的是,SDC沙盒加密系统以其革命性的安全理念和先进技术,为企业提供了一个更可靠、更高效的数据保护方案。 传统加密方案…...

SVN——常见问题
基本操作 检出 提交 更新 显示日志 撤销本地修改 撤销已提交内容 恢复到指定版本 添加忽略 修改同一行 修改二进制文件...

JavaCV 图像灰度化处理
🧑 博主简介:历代文学网(PC端可以访问:https://literature.sinhy.com/#/literature?__c1000,移动端可微信小程序搜索“历代文学”)总架构师,15年工作经验,精通Java编程,…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
