代码随想录算法训练营第46期Day37,38,39,41
这几天晚上看比赛,就把刷题耽误了。还好是开新章节,前面的题都比较简单。
然后周天做完了又忘记发了
动态规划
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数
Day37前两道题太简单了,我们从第三道题开始
leetcode.746.使用最小花费爬楼梯

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {vector<int> dp(cost.size()+8);//dp数组存储当前点位的最优解dp[0]=0;dp[1]=0;for(int i=2;i<=cost.size();i++){dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);//这是dp公式,到达第i阶的最优解肯定是i-1阶的最优解+从i-1的花费和i-2阶的最有解+从i-2阶段的花费中小的那一个}return dp[cost.size()];}};leetcode.62.不同路径

class Solution {
public:int uniquePaths(int m, int n) {int dp[105][105];dp[0][0]=0;for(int i=1;i<=m;i++){dp[i][1]=1;}for(int i=1;i<=n;i++){dp[1][i]=1;}for(int i=2;i<=m;i++){for(int j=2;j<=n;j++){dp[i][j]=dp[i][j-1]+dp[i-1][j];}}return dp[m][n];}
};leetcode.63.不同路径Ⅱ

class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();int n = obstacleGrid[0].size();vector<vector<int>> dp(m, vector<int>(n, 0));//注意最好用vector容器。都初始化为0/*if(obstacleGrid[0][0]==1||obstacleGrid[m-1][n-1]==1){//如果开始或终点有障碍那直接返回障碍return 0;}*/for(int i=0;i<m;i++){if(obstacleGrid[i][0]==1){//如果在边界的两条线上有障碍,那从障碍开始一下路径数都为0break;}dp[i][0]=1;}for(int i=0;i<n;i++){ if(obstacleGrid[0][i]==1){break;}dp[0][i]=1;}for(int i=1;i<m;i++){for(int j=1;j<n;j++){if(obstacleGrid[i][j]==0)dp[i][j]=dp[i][j-1]+dp[i-1][j];//如果碰不到障碍就进行dp,保证障碍处路径为0}}return dp[m-1][n-1];}
};leetcode.416.分割等和子集

class Solution {
public:bool canPartition(vector<int>& nums) {sort(nums.begin(),nums.end());int sum=0;for(int i=0;i<nums.size();i++){sum+=nums[i];}vector<int> dp(11111,0);//这里数组尽量开大点,不然过不了if (sum % 2 == 1) return false;sum= sum / 2;//能够分成两个子集的元素和相等说明,有一部分元素相加的和是总和的一半//那么元素个数是种类,sum/2是容量的01背包问题就出现了for(int i=0;i<nums.size();i++){for(int j=sum;j>=nums[i];j--){dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);}}if(dp[sum]==sum){return true;}return false;}
};leetcode.1049.最后一块的石头重量

class Solution {
public:
//和分割等和子列类似int lastStoneWeightII(vector<int>& stones) {vector<int> dp(10010,0);int sum=0;for(int i=0;i<stones.size();i++){sum+=stones[i];}int sum1=sum;sum=sum/2;for(int i=0;i<stones.size();i++){for(int j=sum;j>=stones[i];j--){dp[j]=max(dp[j],dp[j-stones[i]]+stones[i]);}}return sum1-2*dp[sum];}
};leetcode.494.目标和
假设加法的总和为x,那么减法对应的总和就是sum - x。
所以我们要求的是 x - (sum - x) = target
x = (target + sum) / 2
此时问题就转化为,用nums装满容量为x的背包,有几种方法
-
不放物品i:即背包容量为j,里面不放物品i,装满有dp[i - 1][j]中方法。
-
放物品i: 即:先空出物品i的容量,背包容量为(j - 物品i容量),放满背包有 dp[i - 1][j - 物品i容量] 种方法。
-
if (nums[i] > j) dp[i][j] = dp[i - 1][j]; //说明背包容量装不下 物品i,所以此时装满背包的方法值 等于 不放物品i的装满背包的方法,
- 举例推导dp数组
输入:nums: [1, 1, 1, 1, 1], target: 3
bagSize = (target + sum) / 2 = (3 + 5) / 2 = 4
dp数组状态变化如下

那么最上行dp[0][j] 如何初始化呢?
dp[0][j]:只放物品0, 把容量为j的背包填满有几种方法。
只有背包容量为 物品0 的容量的时候,方法为1,正好装满。
其他情况下,要不是装不满,要不是装不下。
所以初始化:dp[0][nums[0]] = 1 ,其他均为0 。
表格最左列也要初始化,dp[i][0] : 背包容量为0, 放物品0 到 物品i,装满有几种方法。
都是有一种方法,就是放0件物品。
即 dp[i][0] = 1
如果有两个物品,物品0为0, 物品1为0,装满背包容量为0的方法有几种。
- 放0件物品
- 放物品0
- 放物品1
- 放物品0 和 物品1
此时是有4种方法。
其实就是算数组里有t个0,然后按照组合数量求,即 2^t
遍历顺序
在明确递推方向时,我们知道 当前值 是由上方和左上方推出。
那么我们的遍历顺序一定是 从上到下,从左到右。
因为只有这样,我们才能基于之前的数值做推导。
for (int i = 0; i < nums.size(); i++) {if (nums[i] == 0) numZero++;dp[i][0] = (int) pow(2.0, numZero);}class Solution {
public:
int count=0;int findTargetSumWays(vector<int>& nums, int target) {int sum=0;for(int i=0;i<nums.size();i++){sum+=nums[i]; }if (abs(target) > sum) return 0; sum+=target;if(sum%2==1){return 0;} sum=sum/2;int bagSize=sum;vector<vector<int>> dp(nums.size(), vector<int>(10010, 0));// 初始化最上行if (nums[0] <= bagSize) dp[0][nums[0]] = 1; // 初始化最左列,最左列其他数值在递推公式中就完成了赋值dp[0][0] = 1; int numZero = 0;for (int i = 0; i < nums.size(); i++) {if (nums[i] == 0) numZero++;dp[i][0] = (int) pow(2.0, numZero);}// 以下遍历顺序行列可以颠倒for (int i = 1; i < nums.size(); i++) { // 行,遍历物品for (int j = 0; j <= bagSize; j++) { // 列,遍历背包if (nums[i] > j) dp[i][j] = dp[i - 1][j]; else dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];}}return dp[nums.size() - 1][bagSize];}
};一维数组版
二维DP数组递推公式: dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
去掉维度i 之后,递推公式:dp[j] = dp[j] + dp[j - nums[i]] ,即:dp[j] += dp[j - nums[i]]
遍历物品放在外循环,遍历背包在内循环,且内循环倒序(为了保证物品只使用一次)。

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0;for (int i = 0; i < nums.size(); i++) sum += nums[i];if (abs(target) > sum) return 0; // 此时没有方案if ((target + sum) % 2 == 1) return 0; // 此时没有方案int bagSize = (target + sum) / 2;vector<int> dp(bagSize + 1, 0);dp[0] = 1;for (int i = 0; i < nums.size(); i++) {for (int j = bagSize; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[bagSize];}
};深搜遍历做法
class Solution {
public:
int count=0;void backtrack(vector<int>& nums,int target,int index,int sum){if(index==nums.size()){if(sum==target){count++;}}else{backtrack(nums,target,index+1,sum+nums[index]);backtrack(nums,target,index+1,sum-nums[index]);}}int findTargetSumWays(vector<int>& nums, int target) {backtrack(nums,target,0,0);return count; }
};leetcode.474.一零和..

本题中strs 数组里的元素就是物品,每个物品都是一个!
而m 和 n相当于是一个背包,两个维度的背包。
理解成多重背包的同学主要是把m和n混淆为物品了,感觉这是不同数量的物品,所以以为是多重背包。
但本题其实是01背包问题!
只不过这个背包有两个维度,一个是m 一个是n,而不同长度的字符串就是不同大小的待装物品。
开始动规五部曲:
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。
- 确定递推公式
dp[i][j] 可以由前一个strs里的字符串推导出来,strs里的字符串有zeroNum个0,oneNum个1。
dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
然后我们在遍历的过程中,取dp[i][j]的最大值。
所以递推公式:dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
此时大家可以回想一下01背包的递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
对比一下就会发现,字符串的zeroNum和oneNum相当于物品的重量(weight[i]),字符串本身的个数相当于物品的价值(value[i])。
这就是一个典型的01背包! 只不过物品的重量有了两个维度而已。
- dp数组如何初始化
01背包的dp数组初始化为0就可以。
因为物品价值不会是负数,初始为0,保证递推的时候dp[i][j]不会被初始值覆盖。
- 确定遍历顺序
01背包一定是外层for循环遍历物品,内层for循环遍历背包容量
那么本题也是,物品就是strs里的字符串,背包容量就是题目描述中的m和n。(相当于之前的一维dp,采用了滚动数组)
倒序遍历是为了保证物品i只被放入一次!。但如果一旦正序遍历了,那么物品0就会被重复加入多次!
那么问题又来了,为什么二维dp数组遍历的时候不用倒序呢?
因为对于二维dp,dp[i][j]都是通过上一层即dp[i - 1][j]计算而来,本层的dp[i][j]并不会被覆盖!

class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // 默认初始化0for (string str : strs) { // 遍历物品int oneNum = 0, zeroNum = 0;for (char c : str) {if (c == '0') zeroNum++;else oneNum++;}for (int i = m; i >= zeroNum; i--) { // 遍历背包容量且从后向前遍历!for (int j = n; j >= oneNum; j--) {dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
};相关文章:

代码随想录算法训练营第46期Day37,38,39,41
这几天晚上看比赛,就把刷题耽误了。还好是开新章节,前面的题都比较简单。 然后周天做完了又忘记发了 动态规划 确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数 Day37前两道题太简单…...

点跟踪论文—RAFT: Recurrent All-Pairs Field Transforms for Optical Flow-递归的全对场光流变换
点目标跟踪论文—RAFT: Recurrent All-Pairs Field Transforms for Optical Flow-递归的全对场光流变换 读论文RAFT密集光流跟踪的笔记 RAFT是一种新的光流深度网络结构,由于需要基于点去做目标的跟踪,因此也是阅读了像素级别跟踪的一篇ECCV 2020的经典…...

jmeter学习(6)逻辑控制器-循环
循环执行 1、循环读取csv文件的值 2、foreach 读取变量,变量数字后缀有序递增,通过counter实现 ${__V(typeId${typeIdNum})} beansell断言 String typeIdNum vars.get("typeIdNum"); String response prev.getResponseDataAsString(); …...

unity学习笔记-安装与部署
unity学习笔记-安装与部署 unity & visual studio下载unityvisual studio 创建工程项目内的布局介绍初始化项目各目录介绍1. 场景视图(Scene)2. 游戏视图(Game)3. 层次结构视图(Hierarchy)4. 检查器视图…...

Django+MySQL接口开发完全指南
前言 本文将详细介绍如何使用Django结合MySQL数据库开发RESTful API接口。我们将从环境搭建开始,一步步实现一个完整的接口项目。 环境准备 首先需要安装以下组件: Python 3.8Django 4.2MySQL 8.0mysqlclientdjangorestframework 安装命令 # 创建虚…...

CentOS7上下载安装 Docker Compose
Docker Compose简要介绍(想直接看安装步骤的请跳转到[必要的安装步骤]) Docker Compose 是一个用于定义和管理多容器 Docker 应用的工具,它可以通过一个简单的 YAML 文件(docker-compose.yml)来配置应用程序的服务、网…...

虚拟机的 NAT 模式 或 Bridged 模式能够被外界IPping通
如果虚拟机使用的是 NAT 模式 或 Bridged 模式,通常可以让外部网络(例如互联网)访问虚拟机。NAT 和 Bridged 模式的不同之处在于它们如何将虚拟机连接到宿主机和外部网络。以下是这两种模式的详细说明: 1. NAT 模式 在 NAT 模式…...

C# 使用Dll的几种方法举例
使用 DLL(动态链接库)是 C# 开发中常见的任务之一。DLL 文件包含可以在运行时加载的代码和数据,允许程序共享功能和资源,降低程序的内存占用并促进代码的复用。本篇文章将深入探讨 C# 中使用 DLL 的多种方法,并提供相关…...

什么是不同类型的微服务测试?
大家好,我是锋哥。今天分享关于【什么是不同类型的微服务测试?】面试题?希望对大家有帮助; 什么是不同类型的微服务测试? 1000道 互联网大厂Java工程师 精选面试题-Java资源分享网 微服务架构中的测试可以分为多种类…...
)
Docker 拉取镜像时配置可用镜像源(包含国内可用镜像源)
在/etc/docker/daemon.json中写入如下内容(如果文件不存在请新建该文件): { "registry-mirrors":["https://registry.docker-cn.com"] } 重新加载 json 配置文件: sudo systemctl daemon-reload重启 docker 服务: sud…...

International Symposium on Artificial Intelligence Innovations
计算机科学(Computer Science): 算法、自动化软件工程、生物信息学和科学计算、计算机辅助设计、计算机动画、计算机体系结构、计算机建模、计算机网络、计算机安全、计算机图形学与图像处理、数据库与数据挖掘、数据压缩、数据加密、数字信号…...

Golang笔记_day10
Go面试题(三) 1、什么是channel,为什么它可以做到线程安全 在Go语言中,channel是一种类型,它可以用来在协程之间传递数据通过共享内存来通信: 通过共享内存来通信是指多个线程或进程直接访问相同的内存区域…...

mlir learn
https://github.com/j2kun/mlir-tutorial 学习这个项目 https://www.jeremykun.com/2023/08/10/mlir-getting-started/ get start 用我的mac编译一下试试看 然后遇到架构不对的问题 因为他的提交默认是x86 https://github.com/j2kun/mlir-tutorial/pull/1/commits/5a267e269d57…...
)
Windows安装RabbitMQ 4.0.2(图文教程)
本章教程,主要记录在Windows 10上RabbitMQ 4.0.2的安装过程。 一、下载安装包 1、官方下载(速度不稳定) Erlang:https://github.com/erlang/otp/releases/download/OTP-26.0/otp_win64_26.0.exe RabbitMQ 4.0.2:https://github.com/rabbitmq/rabbitmq-server/releases/do…...
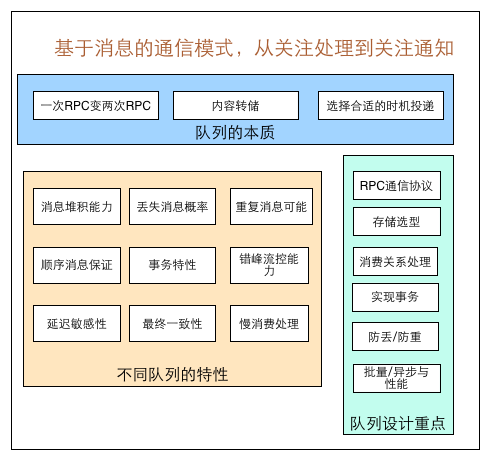
分布式系统中为什么需要使用消息队列
本文转载自 linkedkeeper.com 消息队列已经逐渐成为企业IT系统内部通信的核心手段。它具有低耦合、可靠投递、广播、流量控制、最终一致性等一系列功能,成为异步RPC的主要手段之一。 当今市面上有很多主流的消息中间件,如老牌的ActiveMQ、RabbitMQ&#…...

Linux环境配置(学生适用)
1.挑选最便宜的云服务器 如腾讯云服务器,华为云服务器,百度云服务器等等…… 2.找到你的云服务器实例,然后找到你的公网IP。 3.云服务器实例 ---更多 --- 重置root密码 (一定要重置) 4. 下载并安装 xshell 或者其他登陆软件 xshel…...

麦禾软件:Mac用户找免费开源工具的最佳选择
抖知书老师推荐: 麦禾软件已经成为众多Mac用户的必备平台,尤其对于那些经常寻找免费、开源、正版软件的用户来说,绝对是一个福音。随着科技的不断进步和用户需求的提升,安全、便捷的软件下载体验成为用户选择平台的核心标准。而…...

OpenCV4.8 开发实战系列专栏之 08 - 通道分离与合并
大家好,欢迎大家学习OpenCV4.8 开发实战专栏,长期更新,不断分享源码。 专栏代码全部基于C 与Python双语演示,专栏答疑群 请联系微信 OpenCVXueTang_Asst 本文关键知识点: OpenCV中默认imread函数加载图像文件&#…...
iOS 18.1 RC 版本发布,修复iPhone16随机重启、浏览视频卡顿等bug
今日,苹果发布 iOS 18.1 RC 版本升级,内部版本号为 22B82。 iOS 18.1 RC 也就是 iOS 18.1 准正式版,如果没有大的 Bug,这将是 iOS 18.1 正式版发布前最后一次更新,正式版预计下周向消费者推送。 该 RC 版除了为海外用…...

安装buildkit,并使用buildkit构建containerd镜像
背景 因为K8s抛弃Docker了,所以就只装了个containerd,这样就需要一个单独的镜像构建工具了,就用了buildkit,这也是Docker公司扶持的,他们公司的人出来搞的开源工具,官网在 https://github.com/moby/buildkit 简介 服务端为buildkitd,负责和runc或containerd后端连接干活,目前…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
