算法题总结(十五)——贪心算法(下)
1005、K 次取反后最大化的数组和
给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组:
- 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。
以这种方式修改数组后,返回数组 可能的最大和 。
示例 1:
输入:nums = [4,2,3], k = 1
输出:5
解释:选择下标 1 ,nums 变为 [4,-2,3] 。
示例 2:
输入:nums = [3,-1,0,2], k = 3
输出:6
解释:选择下标 (1, 2, 2) ,nums 变为 [3,1,0,2] 。
class Solution {public int largestSumAfterKNegations(int[] nums, int k) {// 排序,把可能有的负数排到前面Arrays.sort(nums);int sum = 0;for (int i = 0; i < nums.length; i++) {// 贪心:如果是负数,而k还有盈余,就把负数反过来if (nums[i] < 0 && k > 0) {nums[i] = -1 * nums[i];k--;}sum += nums[i];}Arrays.sort(nums);// 如果k没剩,那说明能转的负数都转正了,已经是最大和,返回sum,此时k等于0// 如果k有剩,说明负数已经全部转正,所以如果k还剩偶数个就自己抵消掉,不用删减,如果k还剩奇数个就减掉2倍最小正数。return sum - (k % 2 == 0 ? 0 : 2 * nums[0]); }
}
134、加油站
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。
i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i]区间都不能作为起始位置,因为这个区间选择任何一个位置作为起点,到i这里都会断油,那么起始位置从i+1算起,再从0计算curSum。
有没有可能从[0, i]区间的某一位置开始,也可以有起始位置?,即curSum大于0
如图:
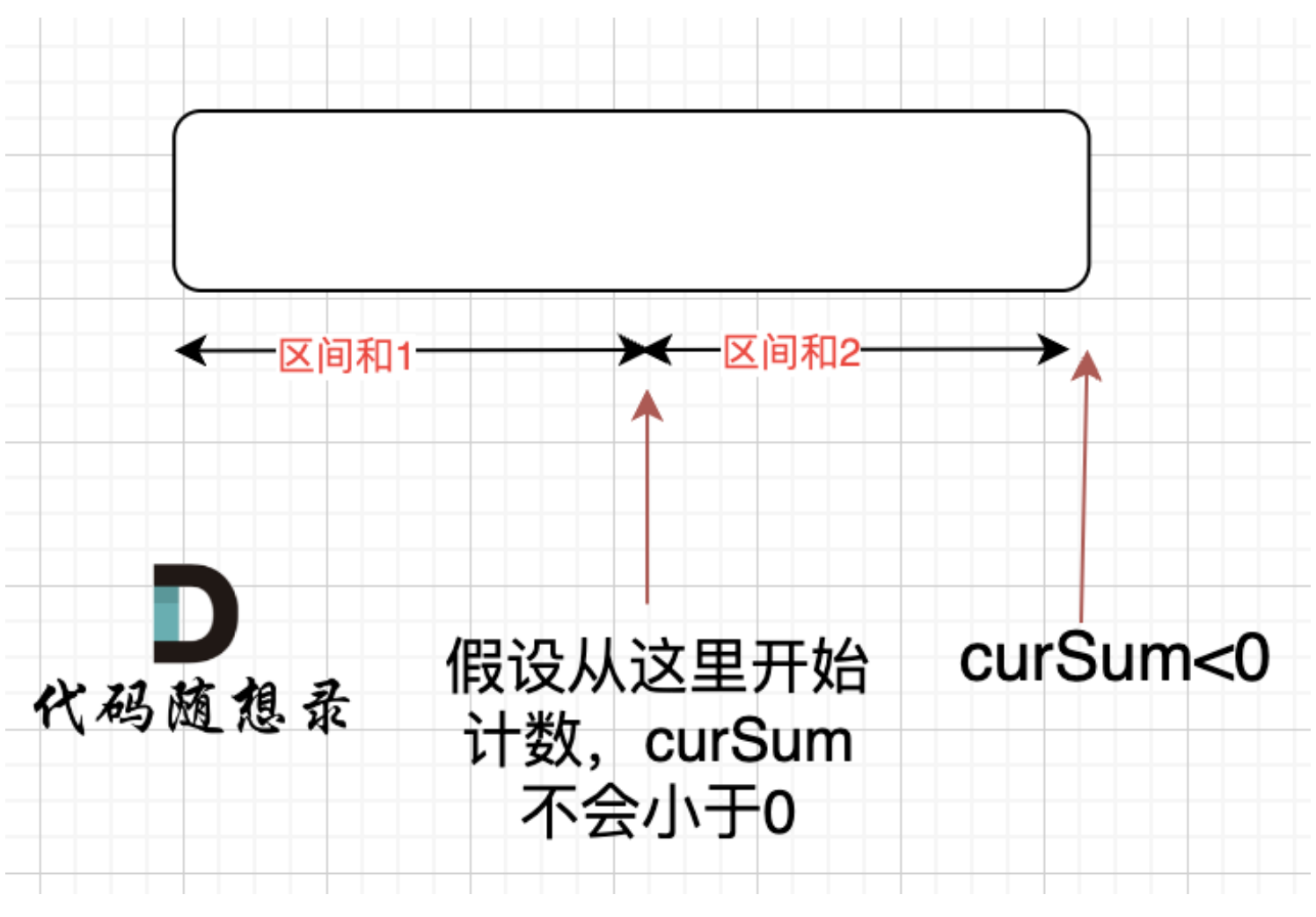
如果 curSum<0 说明 区间和1 + 区间和2 < 0, 那么 假设从上图中的位置开始计数curSum不会小于0的话,就是 区间和2>0。
区间和1 + 区间和2 < 0 同时 区间和2>0,只能说明区间和1 < 0, 那么就会从假设的箭头初就开始从新选择其实位置了。即如果可以作为起始位置,我们在i之前就会把它作为起始位置了
那么局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置
class Solution {public int canCompleteCircuit(int[] gas, int[] cost) {int curSum=0;int totalSum=0;int start=0;for(int i=0;i<gas.length;i++)totalSum+=gas[i]-cost[i];if(totalSum<0)return -1;for(int i=0;i<gas.length;i++){curSum+=gas[i]-cost[i];if(curSum<0){start=i+1;curSum=0;}}return start;}
}
135、分发糖果
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
- 每个孩子至少分配到 1 个糖果。
- 相邻两个孩子评分更高的孩子会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
示例 1:
输入:ratings = [1,0,2]
输出:5
解释:你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。
示例 2:
输入:ratings = [1,2,2]
输出:4
解释:你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。第三个孩子只得到 1 颗糖果,这满足题面中的两个条件。
先确定右边评分大于左边的情况(也就是从前向后遍历)
此时局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果
再确定左孩子大于右孩子的情况(从后向前遍历)
如果 ratings[i] > ratings[i + 1],此时candyVec[i](第i个小孩的糖果数量)就有两个选择了,一个是candyVec[i + 1] + 1(从右边这个加1得到的糖果数量),一个是candyVec[i](之前比较右孩子大于左孩子得到的糖果数量)。
class Solution {public int candy(int[] ratings) {int len =ratings.length;int[] candynum =new int[len];candynum[0]=1;//从左向右比较for(int i=1;i<len;i++){if(ratings[i]>ratings[i-1]){candynum[i]=candynum[i-1]+1;}else{candynum[i]=1;}}//从右向左比较:for(int i=len-2;i>=0;i--){if(ratings[i]>ratings[i+1]){candynum[i]=Math.max(candynum[i],candynum[i+1]+1);}}//统计:int sum=0;for(int i=0;i<candynum.length;i++){sum+=candynum[i];}return sum;}
}
860、柠檬水找零
在柠檬水摊上,每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品,(按账单 bills 支付的顺序)一次购买一杯。
每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付 5 美元。
注意,一开始你手头没有任何零钱。
给你一个整数数组 bills ,其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零,返回 true ,否则返回 false 。
示例 1:
输入:bills = [5,5,5,10,20]
输出:true
解释:
前 3 位顾客那里,我们按顺序收取 3 张 5 美元的钞票。
第 4 位顾客那里,我们收取一张 10 美元的钞票,并返还 5 美元。
第 5 位顾客那里,我们找还一张 10 美元的钞票和一张 5 美元的钞票。
由于所有客户都得到了正确的找零,所以我们输出 true。
逻辑是非常固定的,唯一贪心的点就是尽可能的多留下五元的。
class Solution {public boolean lemonadeChange(int[] bills) {int[] money=new int[2]; //存储剩余的5块和10块的数量for(int i=0;i<bills.length;i++){if(bills[i]==5){money[0]++;}else if(bills[i]==10){if(money[0]>0){money[0]--;money[1]++;} else return false;}else if(bills[i]==20){if(money[0]>0 && money[1]>0){money[0]--;money[1]--;}else if(money[0]>=3){money[0]=money[0]-3;}else{return false;}}}return true;}
}
406、根据身高重建队列
设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列
本题好人分发糖果一样,都是有两个维度!所以要一个一个的来确定!
如果按照k来从小到大排序,排完之后,会发现k的排列并不符合条件,身高也不符合条件,两个维度哪一个都没确定下来。
那么按照身高h来排序呢,身高一定是从大到小排(身高相同的话则k小的站前面),让高个子在前面。
此时我们可以确定一个维度了,就是身高,前面的节点一定都比本节点高!
那么只需要按照k为下标重新插入队列就可以了
例如:

局部最优:优先按身高高的people的k来插入。插入操作过后的people满足队列属性
全局最优:最后都做完插入操作,整个队列满足题目队列属性
people[i] = [hi, ki]表示前面 正好 有 ki 个身高大于或等于 hi 的人。
所以,先按照身高进行排序,然后k来进行插入。
class Solution {public int[][] reconstructQueue(int[][] people) {int[][] result =new int[people.length][];Arrays.sort(people,(a,b)->{if(a[0]==b[0]) return a[1]-b[1]; //身高相同的,让k小的在前面return b[0]-a[0]; //身高不同,按身高降序});LinkedList<int []> list =new LinkedList<>();for(int[] p:people){list.add(p[1],p); //使用LinkedList 来根据位置进行插入}return list.toArray(result);}
}
452、用最少数量的箭引爆气球
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。
一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart</font><font style="color:rgb(51, 51, 51);">,</font><font style="color:rgb(51, 51, 51);background-color:rgb(243, 244, 244);">xend, 且满足 xstart ≤ x ≤ x``end,则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后,可以无限地前进。
给你一个数组 points ,返回引爆所有气球所必须射出的 最小 弓箭数 。
示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]]
输出:2
解释:气球可以用2支箭来爆破:
-在x = 6处射出箭,击破气球[2,8]和[1,6]。
-在x = 11处发射箭,击破气球[10,16]和[7,12]。
示例 2:
输入:points = [[1,2],[3,4],[5,6],[7,8]]
输出:4
解释:每个气球需要射出一支箭,总共需要4支箭。
局部最优:当气球出现重叠,一起射,所用弓箭最少。全局最优:把所有气球射爆所用弓箭最少。
为了让气球尽可能的重叠,需要对数组进行排序。
使用重叠气球最小右边界来 判断是否重叠,只要后面的气球的左边界小于前面重叠气球的最小右边界,就可以使用同一只箭来引爆,另外要注意要收缩后面气球的右边界。
如果气球重叠了,重叠气球中右边边界的最小值 之前的区间一定需要一个弓箭
可以看出首先第一组重叠气球,一定是需要一个箭,气球3,的左边界大于了 第一组重叠气球的最小右边界,所以再需要一支箭来射气球3了。
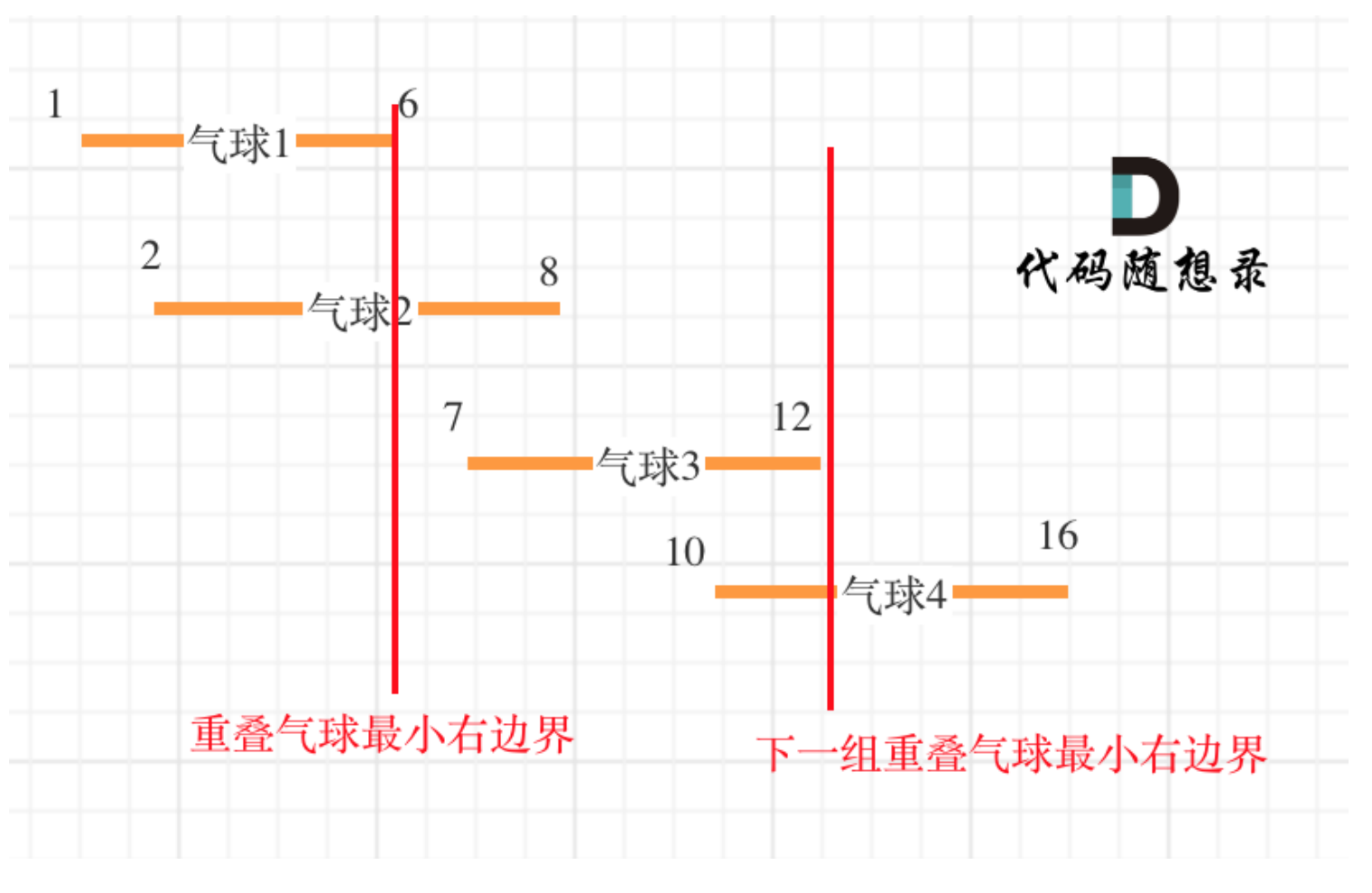
class Solution {public int findMinArrowShots(int[][] points) {// 根据气球直径的开始坐标从小到大排序// 使用Integer内置比较方法,不会溢出Arrays.sort(points,(a,b)->Integer.compare(a[0],b[0]));//Arrays.sort(points,(a,b)->{ return a[0]-b[0];}); 会超时溢出int count=1; //不为空 至少需要一个for(int i=1;i<points.length;i++){if(points[i][0]>points[i-1][1]) //和前面的没有重叠{count++;}else //有重叠,把当前的右边界收缩到最短,这样才能使用同一个箭,弓箭数不需要加{points[i][1]=Math.min(points[i-1][1],points[i][1]);}}return count;}
}
超时: 即最小的int减去最大的int,结果溢出。
435、无重叠区间
给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
示例 1:
输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
本题和前一题思路相同,先排序然后看是否重叠,如果重叠的话count++,并且把intervals[i]的右边界取最小,相当于把右边界大的给移除了
class Solution {public int eraseOverlapIntervals(int[][] intervals) {Arrays.sort(intervals,(a,b)->{return Integer.compare(a[0],b[0]);});int count=0; //用来计算需要移除的区间for(int i=1;i<intervals.length;i++){if(intervals[i][0]>=intervals[i-1][1]) //不重叠{continue;}else{ //重叠count++;//移除,并且右边界取最小的,即右边界大的会被移除intervals[i][1]=Math.min(intervals[i-1][1],intervals[i][1]);}}return count;}
}
763、划分字母区间
给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。
注意,划分结果需要满足:将所有划分结果按顺序连接,得到的字符串仍然是 s 。
返回一个表示每个字符串片段的长度的列表。
示例 1:
输入:s = "ababcbacadefegdehijhklij"
输出:[9,7,8]
解释:
划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的,因为划分的片段数较少。
在遍历的过程中相当于是要找每一个字母的边界,如果找到之前遍历过的所有字母的最远边界,说明这个边界就是分割点了。此时前面出现过所有字母,最远也就到这个边界了。
可以分为如下两步:
- 统计每一个字符最后出现的位置
- 从头遍历字符,并更新字符的最远出现下标,如果找到字符最远出现位置下标和当前下标相等了,则找到了分割点
如图:
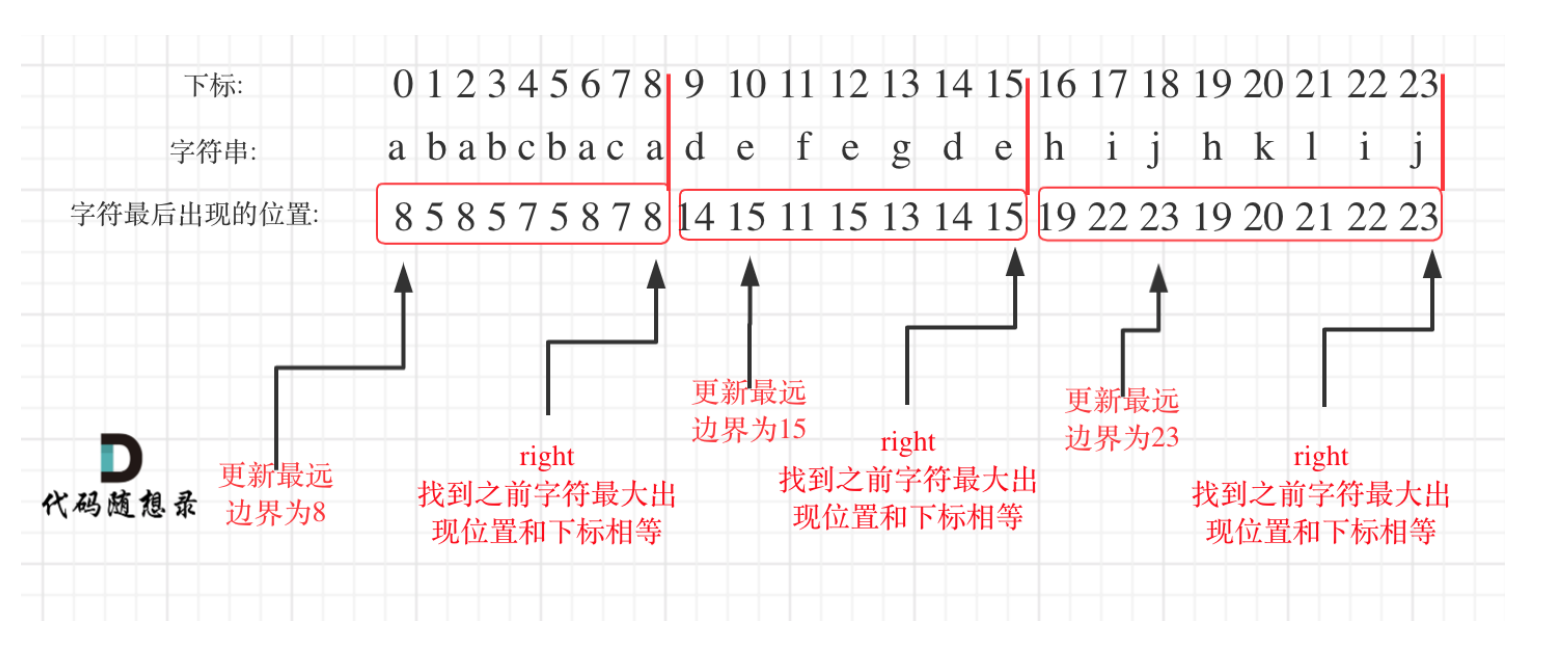
即找到最大的那个字符边界,就是这一段的分割点
class Solution {public List<Integer> partitionLabels(String s) {List<Integer> result =new LinkedList<>();int [] edge =new int [26]; //记录每个字母最后出现的位置char[] chars =s.toCharArray();for(int i=0;i<chars.length;i++){edge[chars[i]-'a']=i; //记录每个字母最后出现的位置}int index=0;int last=0;for(int i=0;i<chars.length;i++){//找到最后出现的最大值,以防止字母在后面还会出现index=Math.max(index,edge[chars[i]-'a']); if(i==index) //如果i就等于最后出现的位置,就可以是分界点了{result.add(index-last+1);last=index+1;}}return result;}
}
56、合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
class Solution {public int[][] merge(int[][] intervals) {List<int[]> result =new LinkedList<>();Arrays.sort(intervals,(a,b)->{return a[0]-b[0];});result.add(intervals[0]);for(int i=1;i<intervals.length;i++){if(intervals[i][0]>intervals[i-1][1]) //没有重叠{result.add(intervals[i]);}else //有重叠的话,要移除前一个{intervals[i][1]=Math.max(intervals[i][1],intervals[i-1][1]);intervals[i][0]=intervals[i-1][0];result.removeLast();result.add(intervals[i]);}}return result.toArray(new int[result.size()][]);}
}
738、单调递增的数字
当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 __单调递增 。
示例 1:
输入: n = 10
输出: 9
示例 2:
输入: n = 1234
输出: 1234
示例 3:
输入: n = 332
输出: 299
例如:98,一旦出现strNum[i - 1] > strNum[i]的情况(非单调递增),首先想让strNum[i - 1]–,然后strNum[i]给为9,这样这个整数就是89,即小于98的最大的单调递增整数。
从前向后遍历的话,遇到strNum[i - 1] > strNum[i]的情况,让strNum[i - 1]减一,但此时如果strNum[i - 1]减一了,可能又小于strNum[i - 2]。
所以要从后向前遍历,就可以重复利用上次比较得出的结果了
class Solution {public int monotoneIncreasingDigits(int n) {String s=String.valueOf(n);char[] chars=s.toCharArray();int start=chars.length;for(int i=chars.length-2;i>=0;i--) //从后向前判断{if(chars[i]>chars[i+1]){chars[i]--;start=i+1; //从最后一个减1的数之后开始都要变为9}}for(int i=start;i<chars.length;i++){chars[i]='9';}//先把chars变为String,在转为Integerreturn Integer.parseInt(String.valueOf(chars));}
}
968、监控二叉树
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
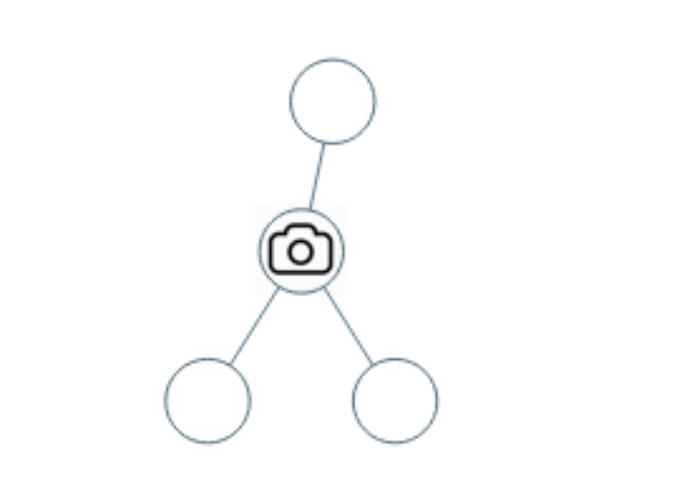
输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
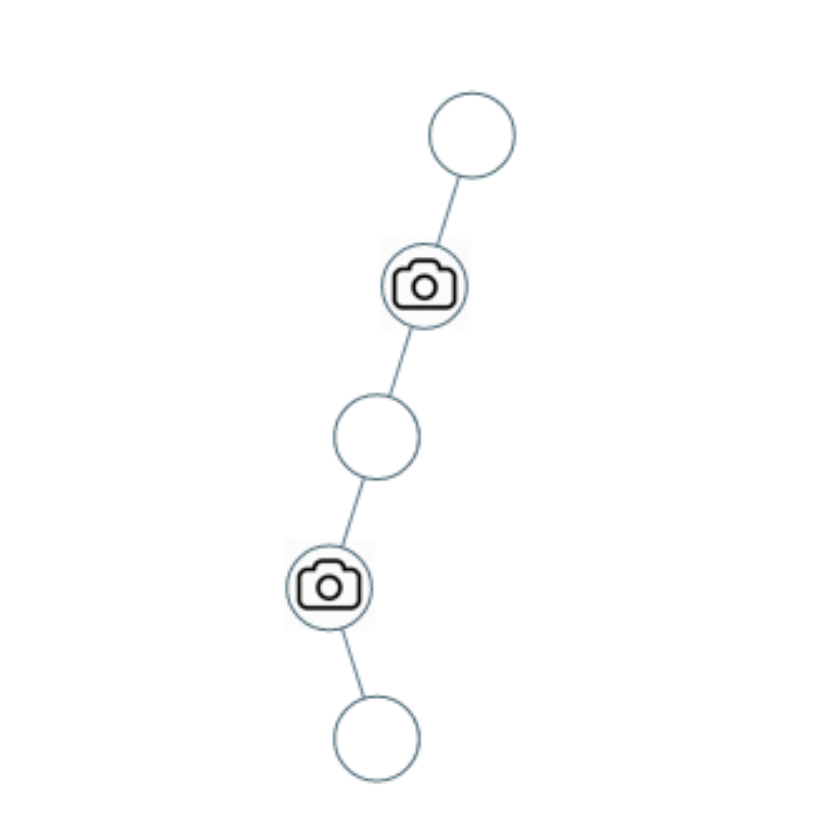
输入:[0,0,null,0,null,0,null,null,0]
输出:2
贪心思想:为了充分利用摄像头的覆盖,要让叶子结点的父节点安装摄像头。
所以我们要从下往上看,局部最优:让叶子节点的父节点安摄像头,所用摄像头最少,整体最优:全部摄像头数量所用最少!
从下到上,所以是后序遍历。
jclass Solution {int res=0;public int minCameraCover(TreeNode root) {// 对根节点的状态做检验,防止根节点是无覆盖状态 .if(minCame(root)==0){res++;}return res;
}
/**节点的状态值:0 表示无覆盖1 表示 有摄像头2 表示有覆盖后序遍历,根据左右节点的情况,来判读 自己的状态*/
public int minCame(TreeNode root){
if(root==null){// 空节点默认为 有覆盖状态,避免在叶子节点上放摄像头return 2;
}
int left=minCame(root.left);
int right=minCame(root.right);// 如果左右节点都覆盖了的话, 那么本节点的状态就应该是无覆盖,没有摄像头
if(left==2&&right==2){//(2,2)return 0;
}else if(left==0||right==0){// 左右节点都是无覆盖状态,那根节点此时应该放一个摄像头// (0,0) (0,1) (0,2) (1,0) (2,0)// 状态值为 1 摄像头数 ++;res++;return 1;
}else{// 左右节点的 状态为 (1,1) (1,2) (2,1) 也就是左右节点至少存在 1个摄像头// 那么本节点就是处于被覆盖状态return 2;
}
}
}
相关文章:

算法题总结(十五)——贪心算法(下)
1005、K 次取反后最大化的数组和 给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组: 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。 重复这个过程恰好 k 次。可以多次选择同一个下标 i 。 以这种方式修改数组后,返回数组 可…...

《深度学习》【项目】自然语言处理——情感分析 <下>
目录 一、了解项目 1、任务 2、文件内容 二、续接上篇内容 1、打包数据,转化Tensor类型 2、定义模型,前向传播函数 3、定义训练、测试函数 4、最终文件格式 5、定义主函数 运行结果: 一、了解项目 1、任务 对微博评论信息的情感分…...

postgresql是国产数据库吗?
PostgreSQL不是国产数据库。但是PostgreSQL对国产数据库的发展有着重要影响,许多国产数据库产品是基于PostgreSQL进行二次开发的。 PostgreSQL的开源特性也是其受欢迎的重要原因之一。开源意味着任何人都可以查看、修改和使用PostgreSQL的源代码。这使得PostgreSQL…...
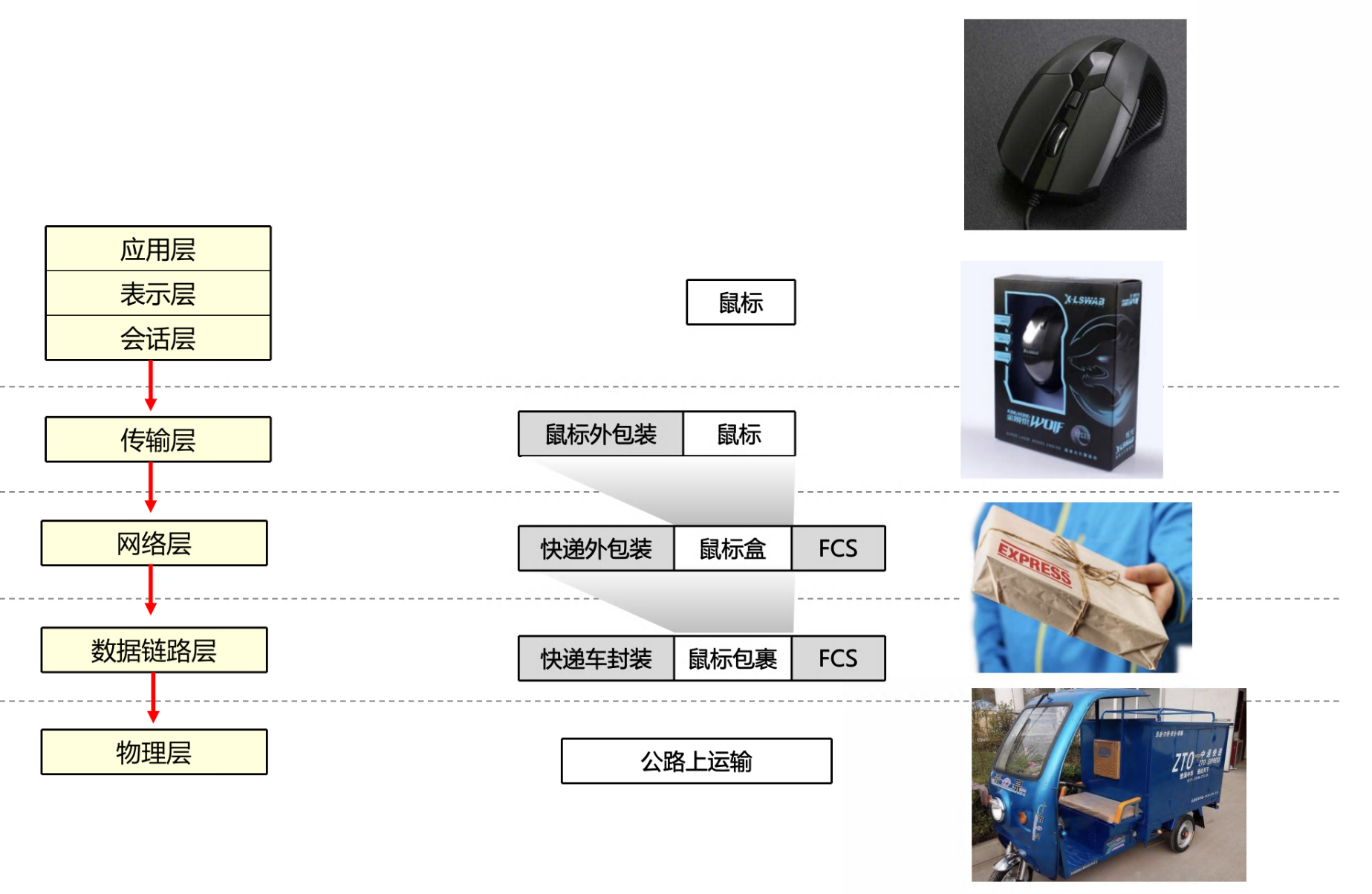
软考——计算机网络概论
文章目录 🕐计算机网络分类1️⃣通信子网和资源子网2️⃣网络拓扑结构3️⃣ 计算机网络分类3:LAN MAN WAN4️⃣其他分类方式 🕑OSI 和 TCP/IP 参考模型1️⃣OSI2️⃣TCP/IP🔴TCP/IP 参考模型对应协议 3️⃣OSI 和 TCP/IP 模型对应…...

01 设计模式-创造型模式-工厂模式
工厂模式(Factory Pattern)是 Java 中最常用的设计模式之一,它提供了一种创建对象的方式,使得创建对象的过程与使用对象的过程分离。 工厂模式提供了一种创建对象的方式,而无需指定要创建的具体类。 通过使用工厂模式…...

ComnandLineRunner接口, ApplcationRunner接口
ComnandLineRunner接口, ApplcationRunner接口 介绍: 这两个接口都有一个run方法,执行时间在容器对象创建好后,自动执行run ( )方法。 创建容器的同时会创建容器中的对象,同时会把容器中的对象的属性赋上值: 举例&…...

Swift用于将String拆分为数组的components与split的区别
根据特定分隔符拆分字符串 在 Swift 中,components(separatedBy:) 和 split(separator:) 都可以用于将字符串拆分为数组,但它们有一些关键区别。下面将从返回值类型、性能和功能等角度进行对比。 1. 返回值类型 components(separatedBy:):…...
)
docker之redis安装(项目部署准备)
创建网络 docker network create net-ry --subnet172.68.0.0/16 --gateway172.68.0.1 redis安装 #创建目录 mkdir -p /data/redis/{conf,data} #上传redis.conf文件到/data/redis/conf文件夹中 #对redis.conf文件修改 # bind 0.0.0.0 充许任何主机访问 # daemonize no #密码 # …...

使用Maven前的简单准备
目录 一、Maven的准备 1、安装jdk1.8或以上版本 2、下载Maven 3、安装Maven 二、Maven目录的分析 三、Maven的环境变量配置 1、设置MAVEN_HOME环境变量 2、设置Path环境变量 3、验证配置是否完成 一、Maven的准备 1、安装jdk1.8或以上版本 jdk的安装 2、下载Maven…...

Java | Leetcode Java题解之第494题目标和
题目: 题解: class Solution {public int findTargetSumWays(int[] nums, int target) {int sum 0;for (int num : nums) {sum num;}int diff sum - target;if (diff < 0 || diff % 2 ! 0) {return 0;}int neg diff / 2;int[] dp new int[neg …...

阅读笔记 Contemporary strategy analysis Chapter 13
来源:Robert M. Grant - Contemporary strategy analysis (2018) Chapter 13 Implementing Corporate Strategy: Managing the Multibusiness Firm Ⅰ Introduction and Objectives 多业务公司 multibusiness firm由多个独立的业务部门组成,如业务单元…...
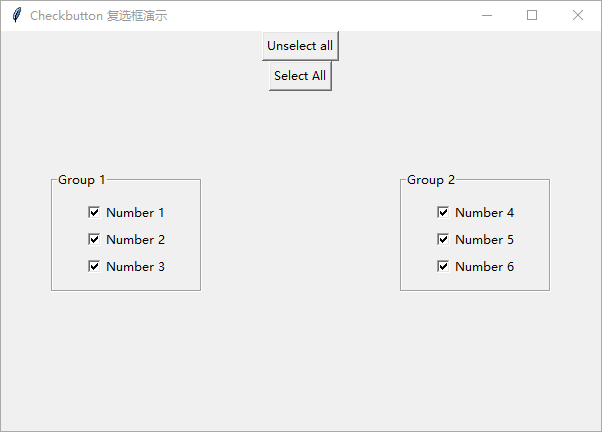
Python GUI 编程:tkinter 初学者入门指南——复选框
在本文中,将介绍 tkinter Checkbox 复选框小部件以及如何有效地使用它。 复选框是一个允许选中和取消选中的小部件。复选框可以保存一个值,通常,当希望让用户在两个值之间进行选择时,可以使用复选框。 要创建复选框,…...

使用vscode导入库失败解决方法
导入库失败原因 在使用vscode写python代码时,有时会遇见导入库失败的情况,如下图:无法解析导入“xxxxx” 或者 运行时报错:ModuleNotFoundError: No module named xxxxx。 原因可能有: 根本没有下载库;…...

无线网卡知识的学习-- mac80211主要代码流程
一 简介概要: mac80211驱动程序作为Linux内核中管理和控制无线网络接口的核心模块,其主要流程涵盖了从数据帧接收到发送的完整过程。 主要覆盖了7个方面: 1. 数据帧接收流程,2. 数据帧发送流程 3. 频道管理和切换 4. 接口管理 5. 安全和认证 6. 管理和调试 7. 注册和初…...

关于k8s集群高可用性的探究
1. k8s的高可用的核心是什么? 说到核心、本质 意味着要从物理层来考虑技术 k8s是一个容器编排管理工具,k8s受欢迎的时机 是docker容器受欢迎时,因为太多的docker容器,管理起来是一个大工程 那么刚好k8s是google自己用了十来年…...

保姆级Pinpoint(APM)实战教程
什么是Pinpoint Pinpoint是由韩国NAVER公司开发并开源的一款应用程序管理工具,主要针对大规模分布式系统进行性能监控和故障诊断。通过跟踪分布式应用程序之间的事务,帮助分析系统的整体结构以及其中的组件是如何相互连接的。 与其对标的还有Twitter的Zi…...

使用SpringBoot自定义注解+AOP+redisson锁来实现防接口幂等性重复提交
1 前提,整合好springboot和redis,redisson的环境 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-aop</artifactId> </dependency> 2 编写自定义注解,注解的作用是标记…...

k8s和ipvs、lvs、ipvsadm,iptables,底层梳理,具体是如何实现的
计算节点的功能: 提供容器运行的环境 kube-proxy的主要功能: 术业有专攻, kube-proxy的主要功能可以概括为4个字 网络规则 那么kube-proxy自己其实是个daemonset控制器跑的 每个节点上都有个的pod 它负责网络规则 其实呢 它还是个小…...

三、归一化与标准化
归一化与标准化 前言一、最小最大值归一化1.1 原理(公式)1.2 API 介绍1.2.1 参数介绍1.2.2 属性介绍1.2.3 注意事项1.2.4 代码演示 1.3 举例说明 二、标准化2.1 原理(公式)2.2 API 介绍2.2.1 参数介绍2.2.2 属性介绍2.2.3 注意事项…...

B2105 矩阵乘法
B2105 矩阵乘法 #include <iostream> using namespace std; int main(){int n,m,k;cin>>n>>m>>k;int arr1[n][m];int arr2[m][k];for(auto & line:arr1){for(auto & x: line){cin>>x;}}for(auto & line:arr2){for(auto & x: lin…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

医疗AI模型可解释性编程研究:基于SHAP、LIME与Anchor
1 医疗树模型与可解释人工智能基础 医疗领域的人工智能应用正迅速从理论研究转向临床实践,在这一过程中,模型可解释性已成为确保AI系统被医疗专业人员接受和信任的关键因素。基于树模型的集成算法(如RandomForest、XGBoost、LightGBM)因其卓越的预测性能和相对良好的解释性…...
