【密码分析学 笔记】ch3 3.1 差分分析
ch3 分组密码的差分分析和相关分析方法
3.1 差分分析
- 评估分组密码安全性通用方法
- 可用于杂凑函数和流密码安全性
预备知识:
- 迭代性分组密码(分组密码一般结构)
- 简化版本 mini-AES CipherFour算法
3.1.1 差分分析原理
现象:密钥在异或运算过程中被抵消 → 直接从明文对异或值得到密文对异或值(绕过密钥)【不随机现象】
差分值: X和X’是两个长度为n的二进制比特串, Δ X = X ⊕ X ′ { ΔX=X \oplus X'} ΔX=X⊕X′ 称为X和X’的差分值
- 模加运算 模减差分
i轮差分、i轮差分对(differential): P β 0 → i 轮 β i {P \beta_{0} \stackrel{i轮}\to \beta_{i} } Pβ0→i轮βi 差分经过i轮的传播特性
i轮差分概率: D P ( β 0 → i 轮 β i ) {DP(\beta_{0} \stackrel{i轮}\to \beta_{i}) } DP(β0→i轮βi)
理想分组密码: α {\alpha} α 是输入差分, β {\beta} β 是输出差分,n是分组长度,理想分组密码满足随机置换, ∀ β ∈ { 0 , 1 } n , D P ( α → i 轮 β ) = 1 / 2 n { \forall \beta \in \{0,1\} ^{n},DP(\alpha \stackrel{i轮}\to \beta)=1/2^{n} } ∀β∈{0,1}n,DP(α→i轮β)=1/2n,构造区分器关键:找到高概率的i轮差分 α → i 轮 β {\alpha \stackrel{i轮}\to \beta} α→i轮β,满足 D P ( α → i 轮 β ) > 1 / 2 n {DP(\alpha \stackrel{i轮}\to \beta)>1/2^{n}} DP(α→i轮β)>1/2n
差分分析原理:
- 发现长轮数、高概率的i轮差分(不随机现象)
- 建立与部分密钥有关的带概率的方程,利用正误密钥下,中间状态满足特定差分值的明密文对数服从不同分布,恢复密钥(分割密钥空间,建立方程组/约束条件,进行密钥恢复攻击)
差分分析攻击模型
假设 D P ( α , β ) = p > 1 / 2 n , ∣ K ~ ∣ = k {DP(\alpha , \beta)=p >1/2^{n},|\widetilde{K}|=k} DP(α,β)=p>1/2n,∣K ∣=k,设置 2 k { 2^{k} } 2k 个计数器,初始化为0
- 采样:选取满足条件的差分明文对
- 去噪:根据β值过滤对应的密文
- 恢复密钥:对方程组每个解都设置1个计数器,处理完所有明文对后从大到小排序,前 2 k − a {2^{k-a}} 2k−a个作为正确密钥候选值,结合穷举攻击等确定正确密钥
3.1.2 CipherFour 算法差分分析
3.1.2.1 各运算部件差分传播特性
CipherFour算法:
- 16bit分组长度
- r轮迭代
- 密钥长度为16(r+1)bits
- 假设轮密钥相互独立
算法每一轮(除最后一轮)包含:
- 16比特的轮密钥异或
- 4个4比特的S盒
- 16比特的比特置换
最后一轮包含:
- 16比特的轮密钥异或
- 4个4比特的S盒
- 16比特的白化密钥异或
1.S盒
非线性变换S盒差分传播概率:
- 输入差分α过S盒后变为输出差分β,记为** α → S β {\alpha \stackrel{S}\to \beta} α→Sβ**
- 满足 α → S β {\alpha \stackrel{S}\to \beta} α→Sβ 的明文对的个数为** N S ( α , β ) {N_{S}(\alpha,\beta)} NS(α,β)**
- 相应的 α → S β {\alpha \stackrel{S}\to \beta} α→Sβ 的差分传播概率为** D P ( α → S β ) = P r ( α → S β ) = N S ( α , β ) 2 m {DP(\alpha \stackrel{S}\to \beta)=Pr(\alpha \stackrel{S}\to \beta)=\frac{N_{S}(\alpha,\beta)}{2^{m}} } DP(α→Sβ)=Pr(α→Sβ)=2mNS(α,β)**
S盒差分分布表(DDT)
- 构造:α为行标,β为列标,行列交错处的项为 N S ( α , β ) {N_{S}(\alpha,\beta)} NS(α,β),构造的 2 m × 2 n {2^{m}×2^{n}} 2m×2n的表
- CipherFour的DDT特性
- D P ( 0 x 0 → S 0 x 0 ) = 1 {DP(0x0 \stackrel{S}\to 0x0)=1} DP(0x0→S0x0)=1
- D P ( 0 x 0 → S 0 x i ) = 1 , i ≠ 0 {DP(0x0 \stackrel{S}\to 0xi)=1,i\neq0} DP(0x0→S0xi)=1,i=0
- 若 N S ( α , β ) = 0 {N_{S}(\alpha,\beta)=0} NS(α,β)=0,记作 α ↛ β {\alpha \nrightarrow \beta} α↛β
- 如 D P ( 0 x f → S 0 x 1 ) = 0 {DP(0xf \stackrel{S}\to 0x1)=0} DP(0xf→S0x1)=0
- 对随机置换RP(Random Permutation)
- P r ( α → R P β ) = 1 2 4 {Pr(\alpha \stackrel{RP}\to \beta)=\frac{1}{2^{4}}} Pr(α→RPβ)=241
- DDT中的数都是偶数
2.P置换
拉线操作,只改变bit位置,不改变取值
输出差分等于输入差分经过P置换后的结果
P ( X ) ⊕ P ( X ′ ) = P ( X ⊕ X ′ ) {P(X)\oplus P(X')=P(X \oplus X')} P(X)⊕P(X′)=P(X⊕X′)
3.异或密钥AK
( X ⊕ K ) ⊕ ( X ′ ⊕ K ) = X ⊕ X ′ {(X\oplus K)\oplus (X'\oplus K)=X \oplus X'} (X⊕K)⊕(X′⊕K)=X⊕X′
输出差分等于输入差分
总结可得,差分在各部件的传播特性为:
- 过线性变换差分值确定
- 异或密钥差分值不变
- 过非线性变换差分值不确定,传播概率由S盒DDT决定
3.1.2.2 CipherFour算法的多轮差分路线
i轮差分路线 β 0 → 1 轮 β 1 → 1 轮 β 2 → 1 轮 . . . → 1 轮 β i {\beta_{0}\stackrel{1轮}\to \beta_{1}\stackrel{1轮}\to \beta_{2}\stackrel{1轮}\to... \stackrel{1轮}\to\beta_{i}} β0→1轮β1→1轮β2→1轮...→1轮βi
i轮差分路线概率
- 分组密码输入X以及轮密钥取值相互独立且均匀分布
- 等于各轮差分路线概率乘积
- D P ( β 0 → 1 轮 β 1 → 1 轮 β 2 → 1 轮 . . . → 1 轮 β i ) = ∏ j = 1 i D P ( β j − 1 → 1 轮 β j ) {DP(\beta_{0}\stackrel{1轮}\to \beta_{1}\stackrel{1轮}\to \beta_{2}\stackrel{1轮}\to... \stackrel{1轮}\to\beta_{i})=\prod \limits_{j=1}^iDP(\beta_{j-1}\stackrel{1轮}\to \beta_{j})} DP(β0→1轮β1→1轮β2→1轮...→1轮βi)=j=1∏iDP(βj−1→1轮βj)
i轮最优差分路线
- 所有i轮差分路线中概率最大的(可能不止一条)
活跃S盒
- 输入差分非零的S盒
影响i轮差分路线概率的主要因素
- 活跃S盒个数
- 活跃S盒对应的输出差分
CipherFour 1轮最优差分路线
- 需要活跃S盒的个数≥1,由DDT表可得,
- D P ( 0 x F → S 0 x D ) = 10 2 4 = 5 8 {DP(0xF \stackrel{S}\to 0xD)=\frac{10}{2^{4}}=\frac{5}{8}} DP(0xF→S0xD)=2410=85
2轮最优差分路线与1轮最优无关
- 直接以1轮最优差分路线的输出差分为输入差分,得到的DP为 5 8 ⋅ ( 3 5 ) 3 ≈ 0.033 {\frac{5}{8}·(\frac{3}{5})^{3}≈0.033} 85⋅(53)3≈0.033
- 保持每轮一个S盒,概率为 D P ( 0 x 2 → S 0 x 2 ) = 6 2 4 = ( 3 8 ) 2 {DP(0x2 \stackrel{S}\to 0x2)=\frac{6}{2^{4}}=(\frac{3}{8})^{2}} DP(0x2→S0x2)=246=(83)2,更优
差分路线级联
迭代型差分概率
- 给定概率为 p i {p_{i}} pi的i轮差分路线 β 0 → 1 轮 β 1 → 1 轮 β 2 → 1 轮 . . . → 1 轮 β i {\beta_{0}\stackrel{1轮}\to \beta_{1}\stackrel{1轮}\to \beta_{2}\stackrel{1轮}\to... \stackrel{1轮}\to\beta_{i}} β0→1轮β1→1轮β2→1轮...→1轮βi,若 β 0 = β i {\beta_{0}=\beta_{i}} β0=βi,迭代该路线k次,得到一条ki轮的差分路线 β 0 → 1 轮 β 1 → 1 轮 . . . → 1 轮 β 0 → 1 轮 β 1 → 1 轮 . . . → 1 轮 β 0 {\beta_{0}\stackrel{1轮}\to \beta_{1}\stackrel{1轮}\to ...\stackrel{1轮}\to\beta_{0}\stackrel{1轮}\to \beta_{1} \stackrel{1轮}\to ... \stackrel{1轮}\to\beta_{0}} β0→1轮β1→1轮...→1轮β0→1轮β1→1轮...→1轮β0
3.1.2.3 CipherFour算法的多轮差分
实验得到i轮差分概率大于单条差分路线的概率。
没有必要固定中间状态的差分
(基于独立性假设)r轮差分的概率
- 共s条输入差分为 β 0 {\beta_{0}} β0,输出差分为 β i {\beta_{i }} βi的i轮差分路线
D P ( b e t a 0 → i 轮 β 1 ) = ∑ t = 1 s D P ( β 0 → 1 轮 β 1 t → . . . → β i − 1 t → 1 轮 β i t ) = ∑ t = 1 s ( ∏ j = 1 i D P ( β j − 1 t → 1 轮 β j t ) ) DP(beta_{0}\stackrel{i轮}\to \beta_{1})=\sum\limits_{t=1}^{s}DP(\beta_{0}\stackrel{1轮}\to \beta_{1}^{t}\to ... \to \beta_{i-1}^{t}\stackrel{1轮}\to\beta_{i}^{t}) \\=\sum\limits_{t=1}^{s}\big (\prod\limits_{j=1}^{i}DP(\beta_{j-1}^{t}\stackrel{1轮}\to\beta_{j}^{t}) \big) DP(beta0→i轮β1)=t=1∑sDP(β0→1轮β1t→...→βi−1t→1轮βit)=t=1∑s(j=1∏iDP(βj−1t→1轮βjt))
Markov密码算法:满足独立性假设的算法
通过不随机现象区分4轮CipherFour算法和随机置换 0.08>0.000015
3.1.2.4 5轮CipherFour算法的密钥恢复攻击
5轮等于4轮CipherFour算法+1 “4+1”
4轮加密后的输出是 中间变量,猜测 k 5 {k_{5}} k5的取值
- 采样
- 选择m对满足输入差分的输入对,计算5轮加密后的密文对
- 去噪
- 筛选并删除错误对
- 若四轮加密后中间状态为(0,0,2,0),由DDT得到 ( 0 , 0 , 2 , 0 ) → S ( 0 , 0 , h , 0 ) , h ∈ 1 , 2 , 9 , a {(0,0,2,0) \stackrel{S}\to (0,0,h,0), h∈{1,2,9,a}} (0,0,2,0)→S(0,0,h,0),h∈1,2,9,a
- 正确对相应的密文差分只有四种可能 (0,0,1,0), (0,0,2,0), (0,0,9,0), (0,0,a,0)
- 恢复密钥
- 解方程 S − 1 ( k 5 , 2 ⊕ c 2 ) ⊕ S − 1 ( k 5 , 2 ⊕ c 2 ′ ) = 2 {S^{-1}(k_{5,2}\oplus c_{2})\oplus S^{-1}(k_{5,2}\oplus c_{2}^{'})=2} S−1(k5,2⊕c2)⊕S−1(k5,2⊕c2′)=2,并对每个解设置计数器
- 按计数器取值由大到小对去噪的明文对进行排序,前 2 4 − a {2^{4-a}} 24−a个作为正确密钥的候选值
- 恢复4-bit k 5 , 2 {k_{5,2}} k5,2,实现分割
- 剩余密钥差分或者穷举
正确对:
- 一定满足区分器的头尾差分
- 代入S盒有关方程 解一定包括正确密钥
错误对:
- 一定不满足区分器的头部或尾部差分
- 代入S盒有关方程 解只包含错误密钥
复杂度:重要的是选择明文的个数
信噪比 S N {S_{N}} SN
-
正确密钥(信息)的计数/错误密钥(噪声)的平均计数
-
1 ≤ S N {S_{N}} SN ≤2,需保证有20-40正确对 S N {S_{N}} SN较大
-
S N {S_{N}} SN ≥100时,需保证有3-4个正确对
相关文章:

【密码分析学 笔记】ch3 3.1 差分分析
ch3 分组密码的差分分析和相关分析方法 3.1 差分分析 评估分组密码安全性通用方法可用于杂凑函数和流密码安全性 预备知识: 迭代性分组密码(分组密码一般结构)简化版本 mini-AES CipherFour算法 3.1.1 差分分析原理 现象:密…...

Go:strings包的基本使用
文章目录 string前缀和后缀字符串包含判断子字符串或字符在父字符串中出现的位置字符串替换统计字符串出现次数重复字符串修改字符串大小写修剪字符串分割字符串拼接 slice 到字符串 strconv 本篇主要总结的是go中的string包的一些函数的操作讲解 string 在各个语言中&#x…...

uniapp,获取头部高度
头部自定义时候,设置获取安全区域,可以用 uni.getSystemInfoSync();接口。 <view class"statusBar" :style"{height:statusBarHeightpx}"> let SYSuni.getSystemInfoSync(); let statusBarHeightref(SYS.statusBarHeight) …...

开发面试题-更新中...
探迹科技(腾讯面试官) 1.了不了解循环屏障 2.对于java中的线程冲突有多少了解(我要算1加到1亿) 3.mysql调优怎么调(我跟他讲了explain) 4.type中ref,range,const的区别 5.我有1亿的数据量&…...

【Jmeter】jmeter指定jdk版本启动
背景: 因权限问题,不能修改操作系统的环境变量或者因jmeter启动加载的默认jdk8版本低,需要指定jdk XX版本启动Jmeter 解决办法: 进入jmeter bin目录选择jmeter.bat,记事本编辑jmeter.bat, 在最前面添加 set MINIMAL_…...

数据处理利器:图片识别转Excel表格让数据录入变简单
在现代职场中,手动录入数据是一个耗时且容易出错的过程。无论是纸质文件、照片还是截图,繁琐的输入常常让人感到头疼。如何高效地将这些信息转化为电子表格,是许多职场人士面临的挑战。 为了解决这一问题,我们推出了图片识别转Exc…...

【WPF】中Binding的应用
在 WPF (Windows Presentation Foundation) 中,数据绑定是一种强大的机制,它允许你将用户界面(UI)元素的属性与各种数据源关联起来。这种关联可以是单向的、双向的或一次性的。WPF 的数据绑定支持多种数据源,包括普通对…...
)
华为OD机试2024年真题(基站维修工程师)
基站维修工程师(200分) 小王是一名基站维护工程师,负责某区域的基站维护。 某地方有n个基站(1<n<10),已知各基站之间的距离s(0<s<500),并且基站x到基站y的距离,与基站y到基站x的距离并不一定会…...
)
在MySQL中为啥引入批量键访问(Batch Key Access, BKA)
批量键访问(Batch Key Access, BKA) 是 MySQL 在某些情况下用于优化 JOIN 操作的一种技术,特别是在通过索引进行 JOIN 时,它能有效减少查询的随机 I/O。批量键访问优化通过将一批主键或索引键一次性发送给存储引擎来查找匹配的行&…...
)
912.排序数组(归并排序)
目录 题目解法初始数组1. 分解阶段2. 合并阶段结果 为什么要创建长整型ll mid l ((r - l) >> 1);其中的>>是什么意思 题目 给你一个整数数组 nums,请你将该数组升序排列。 你必须在 不使用任何内置函数 的情况下解决问题,时间复杂度为 O…...

使用 cmake 在 x86 系统中为 arm 系统交叉编译程序
原理: 在 x86 系统里使用交叉编译工具链(arm 版 gcc/g)编译程序,然后放在 arm 系统里运行。 arm 版本 使用 lscpu 查看 cpu 架构 版本说明armv732 bitarmv8/arrch6464 bit 安装交叉编译工具链 # 针对 armv7 sudo apt install…...

软考(网工)——网络规划设计
文章目录 🕐综合布线1️⃣结构化布线系统2️⃣综合布线六大子系统3️⃣综合布线物理结构图 🕑网络分析与设计1️⃣网络规划设计模型2️⃣网络流量分析3️⃣网络安全技术措施表4️⃣技术评价 🕒网络结构与功能1️⃣局域网结构类型2️⃣三层架构…...
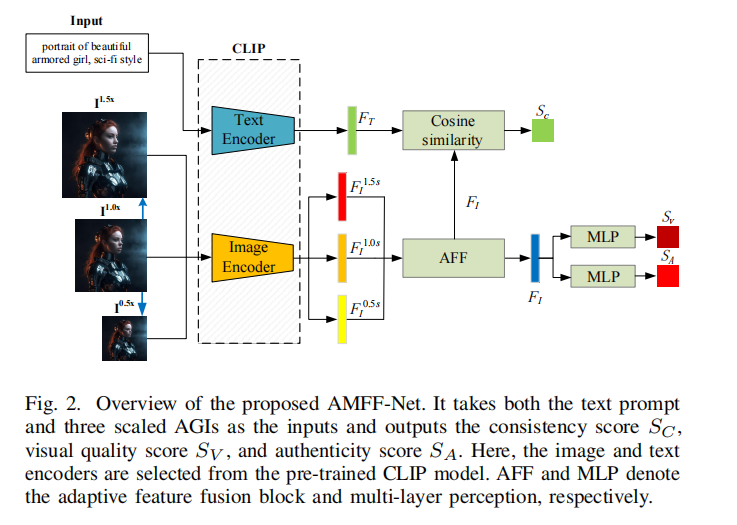
即插即用特征融合模块,即用即涨点!
特征融合(Feature Fusion)是深度学习中的一种重要技术,它可以帮助模型更好地理解数据的内在结构和规律,提高模型的性能和泛化能力。 另外,特征融合还可以提高模型的分类准确率,减少过拟合风险,…...

蓝桥算法双周赛 第 19 场 小白入门赛
打开石门 只要有相连的一样字母就可以消成一个 string s; int ans;void solve() {cin >> s;int len 0;for (int i 0;i < s.size();i ){if (s[i] L) len ;else //遇到Q{ans (len ? 1 : 0); //消除累计的Llen 0;ans ;//遇到Q}}//QLLLL时,最后遇不到Q让累计的L消…...

Cursor零基础小白教程系列「进阶」 - Cursor 智能代码补全详解(Tab)
最适合小白零基础的Cursor教程 网站lookai.top相同作者,最新文章会在网站更新,欢迎收藏书签 Cursor 智能代码补全详解(Tab) 概述 Cursor的智能代码补全,也就是快捷键Tab,是其最强大和独特的AI辅助编程工具之一。本教程将详细介绍…...

数据结构《顺序表》
文章目录 前言一、什么是顺序表?1.1 顺序表的概念1.2 顺序表的建立 二、MyArrayList的实现三、顺序表的方法四、关于顺序表的例子总结 前言 提示:这里涉及到的ArrayList类是一个泛型类,同时后面的很多内容都会涉及到泛型,如果不了…...

视频分享网站毕业设计基于SpringBootSSM框架
目录 1.摘要 2.引言 2.1 研究意义 3 功能描述 3.1功能图展示 3.2非功能需求 4. 需求分析 4.1前端技术 4.2后端技术 4.3视频处理技术 4.4内容分发网络(CDN) 4.5其他关键技术 计算机毕业设计/springboot/javaWEB/J2EE/MYSQL数据库/vue前后…...

Python多进程学习与使用:全面指南
Python多进程学习与使用:全面指南 目录 引言什么是多进程?为什么使用多进程?Python中的多进程模块:multiprocessing创建进程的基本方法进程间通信进程池多进程与多线程的比较常见问题和解决方案最佳实践和性能优化实战项目&…...

HTTP Proxy环境下部署Microsoft Entra Connect和Health Agents
在企业环境中,时常需要通过使用HTTP Proxy访问Internet,在使用HTTP Proxy访问Internet的环境中部署Microsoft Entra Connect和Microsoft Entra Connect Health Agents可能会遇到一些额外的配置步骤,以便这些服务能够正常连接到Internet。 一…...

基于单片机的 OLED 显示终端设计分析与研究
摘要: 我国的经济发展速度正在不断加快,经济体制也在经历着一系列的改革,工业发展也正是受到了它的影响,逐步发生变化。在这样的背景下,传统的 LCD 显示技术,逐渐被显示效果更好,功耗更低的 OLED 代替。本文主要介绍了基于单片机的 OLED 显示终端设计,该设计目前具有很…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...
