当前位置： 首页 > news >正文

基于springboot的网上服装商城推荐系统的设计与实现

news 2025/9/15 7:54:34

基于springboot的网上服装商城推荐系统的设计与实现

开发语言：Java
框架：springboot
JDK版本：JDK1.8
服务器：tomcat7
数据库：mysql 5.7
数据库工具：Navicat11
开发软件：idea

源码获取：
：https://gitee.com/ss-i-gg/Springboot-Online-Clothing-Store-Recommendation-System/blob/master/springboot%E7%BD%91%E4%B8%8A%E6%9C%8D%E8%A3%85%E5%95%86%E5%9F%8E%E6%8E%A8%E8%8D%90%E7%B3%BB%E7%BB%9F%E6%BA%90%E7%A0%81.zip
或者https://download.csdn.net/download/weixin_46115961/89901325

项目介绍:
后端框架使用Springboot+mybatis
前端框架使用Vue+hrml
数据库使用mysql

数据库表设计
在这里插入图片描述
项目开发结构
在这里插入图片描述
系统功能展示
前端用户系统
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
后台管理系统
在这里插入图片描述

用户管理登录
在这里插入图片描述
管理员登录：
在这里插入图片描述
源码获取：网上服装商城推荐系统源码

相关文章：

基于springboot的网上服装商城推荐系统的设计与实现

基于springboot的网上服装商城推荐系统的设计与实现 开发语言：Java 框架：springboot JDK版本：JDK1.8 服务器：tomcat7 数据库：mysql 5.7 数据库工具：Navicat11 开发软件：idea 源码获取&#xf…...

编程日记 2024/10/25 5:25:37

盘古信息IMS系统助力制造企业释放新质生产力

在全球制造业竞争日益激烈的背景下，提升新质生产力已成为制造企业普遍追求的核心目标。因此，众多制造企业开始对生产流程、管理模式乃至整个企业生态系统进行全面的优化与升级，以期在市场竞争中占据优势地位，迎来更广阔的发展空间…...

编程日记 2024/10/25 5:24:35

ArcGIS 10.8 安装教程

目录 一、ArcGIS10.8二、安装链接三、安装教程四、ArcGIS实战 （一）ArcGIS10.8 1. 概述 ArcGIS 10.8是由美国Esri公司开发的GIS平台，用于处理、分析、显示和管理地理数据，并实现数据共享。它具有新特性和功能，性能更…...

编程日记 2024/10/25 5:23:34

Redis学习笔记（二）--Redis的安装与配置

文章目录 一、Redis的安装1、克隆并配置主机2、安装前的准备工作1.安装gcc2.下载Redis3.上传到Linux 3、安装Redis1.解压Redis2.编译3.安装3.查看bin目录 4、Redis启动与停止1.前台启动2.命令式后台启动3.Redis的停止4.配置式后台启动 二、连接前的配置1、绑定客户端IP2、关闭保…...

编程日记 2024/10/25 5:22:33

软件工程之软件系统设计与软件开发方法

一.软件系统设计 1.体系结构设计就是架构设计，软件设计包含4个方面： 接口（人机界面设计）设计：软件与操作系统、软件与人之间如何交互； 架构（结构）设计：定义软件系统各…...

编程日记 2024/10/25 5:21:26

pip命令行安装pytest 一直报错

其实就是切换不同镜像安装 我最终成功的是阿里云镜像 pip install --trusted-host mirrors.aliyun.com pytest 也可以用其他的 pip install -i https://pypi.org/simple pytest # 或者使用其他的镜像源 pip install -i https://pypi.tuna.tsinghua.edu.cn/simple pytest...

编程日记 2024/10/25 5:20:24

如何在Debian操作系统上安装Doker

本章教程，主要介绍如何在Debian 11 系统上安装Docker。主要使用一键安装Docker脚本和一键卸载脚本来完成。 一、安装Docker #!/bin/bashRED\033[0;31m GREEN\033[0;32m YELLOW\033[0;33m BLUE\033[0;34m NC\033[0mCURRENT_DIR$(cd "$(dirname "$0")…...

编程日记 2024/10/25 5:17:16

代码随想录刷题学习日记

仅为个人记录复盘学习历程，解题思路来自代码随想录 代码随想录刷题笔记总结网址:代码随想录 二叉树的迭代遍历(不使用递归实现遍历) 递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，递归是通过栈实现…...

编程日记 2024/10/25 5:16:15

OpenText ALM Octane，为您的 DevOps 管道提供质量保证

实现更高水平的敏捷性、可追溯性和可预测性是一个持续的过程。ALM Octane 可帮助您改进开发和测试流程，从而改善整个软件交付价值流中的工作流程。 产品亮点 对基于软件的创新的需求已经加速，扰乱了几乎每个行业，也改变了我们的生活。快速交…...

编程日记 2024/10/25 5:15:12

【python实操】python小程序之参数化以及Assert（断言）

引言 python小程序之参数化以及Assert（断言） 文章目录 引言一、参数化2.1 题目2.2 代码2.3 代码解释 二、Assert（断言）2.1 概念2.1.1 Assert语句的基本语法：2.1.2 基本断言2.1.3 断言函数参数2.1.4 断言前后状态一致 2…...

编程日记 2024/10/25 5:13:10

探索CSS动画下的按钮交互美学

效果演示 这段代码通过SVG和CSS动画创建了一个具有视觉吸引力的按钮&#xff0c;当用户与按钮交互时&#xff08;如悬停、聚焦或按下&#xff09;&#xff0c;按钮会显示不同的动画效果。 HTML <button class"button"><div class"dots_border"…...

编程日记 2024/10/25 5:11:08

241024-Ragflow离线部署Docker-Rootless环境配置修改

A. 最终效果 B. 文件修改 docker-compose.yml include:- path: ./docker-compose-base.ymlenv_file: ./.envservices:ragflow:depends_on:mysql:condition: service_healthyes01:condition: service_healthyimage: ${RAGFLOW_IMAGE}container_name: ragflow-serverports:- ${…...

编程日记 2024/10/25 5:10:07

网络基础概念：广播域、冲突域与VLAN解析

一、网络基础概念 在现代计算机网络中&#xff0c;广播域、冲突域和虚拟局域网&#xff08;VLAN&#xff09;是网络架构和管理的核心概念。了解这些概念对网络性能优化、流量管理和安全性提升至关重要。 二、广播域 1. 定义 广播域是一个网络逻辑区域&#xff0c;在这个区域…...

编程日记 2024/10/25 5:09:06

【MySQL】C语言连接MySQL数据库3——事务操作和错误处理API

目录 1.MySQL事务处理机制 1.1.autocommit 1.2.autocommit的设置与查看 1.3.使用示例 2.事务操作API 2.1.设置事务提交模式——mysql_autocommit() 2.2.提交事务——mysql_commit() 2.3.事务回滚——mysql_rollback() 3.错误处理的API 3.1.返回错误的描述——mysql_er…...

编程日记 2024/10/25 5:08:04

ARM嵌入式学习--第六天(电子电路基础知识)

电子电路基础知识 -基本元器件 -电阻 电阻&#xff08;Resistance&#xff0c;通常用“R”表示&#xff09;&#xff0c;表示导体对电流的阻碍作用的大小&#xff1b;电阻导体本身的一种特性&#xff1b;超导体没有电阻&#xff0c;作用是用来降压 上拉电阻&#xff1a;将状态…...

编程日记 2024/10/25 5:06:00

JAVA----单例模式

1.单例模式概念&#xff1a; 单例模式是一种设计模式&#xff0c;他的核心是确保一个类只有一个实例&#xff0c;单例模式主要有两种方式&#xff1a;饿汉式与懒汉式 2.饿汉式 饿汉就是一个迫切的意思&#xff0c;类加载就会导致该单实例被创建 饿汉式第一种方式&#xff1a;…...

编程日记 2024/10/25 5:04:58

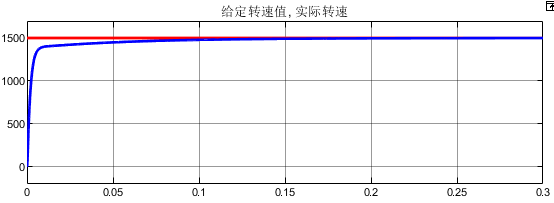
基于递推式最小二乘法的PMSM参数辨识MATLAB仿真模型

微❤关注“电气仔推送”获得资料&#xff08;专享优惠&#xff09; 模型简介 最小二乘法是一种回归估计法&#xff0c;适用于被辨识的参数与系统输出为线性关 系的情况。它是在一定数据量下&#xff0c;基于系统输出误差的平方和最小的准则对参 数进行辨识的方法。此模型通过…...

编程日记 2024/10/25 5:03:57

记录一次部署 k8s 集群无法启动

情况是这样的&#xff0c;k8s 集群&#xff08;v1.31&#xff09;所需要的组件已安装完成&#xff0c;通过 kubeadm init 已经安装部署成功&#xff0c;但是等几分钟&#xff0c;集群组件就一直在重启&#xff0c;查看日志是连接 etcd 超时&#xff0c;所以查看了 etcd 的日志&…...

编程日记 2024/10/25 5:02:56

Linux下MySQL8.x的编译安装与使用

Linux下MySQL的安装与配置 1. 安装环境初始化 1.1 查看是否安装过MySQL 如果使用rpm安装, 检查一下RPM PACKAGE rpm -qa | grep -i mysql # -i 忽略大小写 # 或者 yum list installed | grep mysql如果存在mysql-libs的旧版本包&#xff0c;显示如下 #存在 [rootlocalhost ~]…...

编程日记 2024/10/25 5:01:55

cpuinfo实践记录

py-cpuinfo 是一个用于获取 CPU 信息的 Python 库。它可以帮助你获取 CPU 的详细信息&#xff0c;如 CPU 型号、核心数、频率、缓存大小等。以下是对 py-cpuinfo 模块的详细介绍&#xff1a; 安装 你可以使用 pip 来安装 py-cpuinfo 库&#xff1a; pip install py-cpuinfo …...

编程日记 2024/10/25 4:58:52

web vue 项目 Docker化部署

Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段&#xff1a; 构建阶段&#xff08;Build Stage&#xff09;&#xff1a…...

编程新知 2025/8/12 16:28:43

C++：std::is_convertible

C++标志库中提供is_convertible，可以测试一种类型是否可以转换为另一只类型： template <class From, class To> struct is_convertible; 使用举例： #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

编程新知 2025/6/11 15:23:57

k8s从入门到放弃之Ingress七层负载

k8s从入门到放弃之Ingress七层负载 在Kubernetes&#xff08;简称K8s&#xff09;中&#xff0c;Ingress是一个API对象&#xff0c;它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress&#xff0c;你可…...

编程新知 2025/9/7 0:12:53

1.3 VSCode安装与环境配置

进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件&#xff0c;然后打开终端&#xff0c;进入下载文件夹&#xff0c;键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

编程新知 2025/8/25 22:27:27

【单片机期末】单片机系统设计

主要内容&#xff1a;系统状态机&#xff0c;系统时基&#xff0c;系统需求分析&#xff0c;系统构建&#xff0c;系统状态流图 一、题目要求 二、绘制系统状态流图 题目&#xff1a;根据上述描述绘制系统状态流图&#xff0c;注明状态转移条件及方向。 三、利用定时器产生时…...

编程新知 2025/9/7 11:36:19

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序

一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

编程新知 2025/8/12 6:01:40

3-11单元格区域边界定位(End属性)学习笔记

返回一个Range 对象&#xff0c;只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意&#xff1a;它移动的位置必须是相连的有内容的单元格…...

编程新知 2025/9/7 8:51:17

AI病理诊断七剑下天山，医疗未来触手可及

一、病理诊断困局&#xff1a;刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断"&#xff0c;医生需通过显微镜观察组织切片&#xff0c;在细胞迷宫中捕捉癌变信号。某省病理质控报告显示&#xff0c;基层医院误诊率达12%-15%&#xff0c;专家会诊…...

编程新知 2025/9/7 2:22:03

C++.OpenGL （14/64）多光源（Multiple Lights）

多光源（Multiple Lights） 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

编程新知 2025/6/11 3:15:20

智能AI电话机器人系统的识别能力现状与发展水平

一、引言 随着人工智能技术的飞速发展&#xff0c;AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术&#xff0c;在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

编程新知 2025/6/11 3:05:02