【算法与数据结构】二分查找思想
#1024程序员节|征文#

正文:
二分查找(binary search)是一种基于分治策略的高效搜索算法。它利用数据的有序性,每轮缩小一半搜索范围,直至找到目标元素或搜索区间为空为止,其实有时候数据没有序也能用二分查找思想解题,遇到具体的题我们具体分析。
我们要想搞清楚二分查找的思想是什么就需要结合具体的题目进行理解,单单靠定义是不行的,下面让我们进入刷题的节奏吧!
一、二分查找
704. 二分查找 - 力扣(LeetCode)
给定一个
n个元素有序的(升序)整型数组nums和一个目标值target,写一个函数搜索nums中的target,如果目标值存在返回下标,否则返回-1。
示例 1:输入: nums = [-1,0,3,5,9,12], target = 9 输出: 4 解释: 9 出现在 nums 中并且下标为 4示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2 输出: -1 解释: 2 不存在 nums 中因此返回 -1提示:
- 你可以假设
nums中的所有元素是不重复的。n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
这道题用暴力解法是很好写的,只需从前向后遍历数组,若找到,返回下标,否则返回-1。它的时间复杂度为O(N)。
这道题的题目就是二分查找,我们以这个题为代表引出二分查找的思想。
首先这道题目中的数组是升序的,那么给你一个target目标值,要查找target对应的下标。
我们可以先拿到数组中间的数(nums[mid]),让这个数与target作比较:
1、如果相等,就直接返回它的下标(mid)即可。
2、如果nums[mid]大于target,因为是升序,那么后面的值必定大于target,所以只需在[0,mid-1]这个区间找即可(这样数据的范围就减少一半了)。
3、如果nums[mid]小于target,因为是升序,那么前面的值必定小于target,所以只需在[mid+1,n)这个区间找即可(n为元素个数,这样数据的范围也减少一半)。
如果数据量是100w,比较一次,如果运气好就直接找到,如果运气不好,我比较一次就可以减少50w的数据量,可想而知这个算法如果适合使用,那是非常厉害的。
可能会有人问,可以从1/3的位置或1/4的位置处找一个数进行比较可以吗?
答案是可以的,但是这可能不会太"稳定",以1/3位置为例,运气好可能一次过滤掉大部分数据(3/4),运气不好可能就只过滤掉1/4的数据。
经过大量研究,认为还是取中间的数更优。
回到这题,代码实现:
class Solution {
public:int search(vector<int>& nums, int target) {int left = 0,right=nums.size()-1;while(left <= right) //这里不是"<"而是"<=",因为left==right时对应的值可能就是目标值{int mid = (right-left)/2 + left; //中间位置下标if(nums[mid] > target)right = mid-1; //只需更新rightelse if(nums[mid] < target)left = mid+1; //只需更新leftelsereturn mid;}return -1; //没有找到的情况}
};这道题的代码实现非常简单,但有一个点需要说明一下,就是求中间位置的下标。
一些同学可能会这样写:
int mid = (left + right) / 2;这样写会面临一个问题,当left和right数极大时,它们两个相加可能会超出int最大值,这样计算出的mid就不正确了,我们改写为上面的形式就不会出现"越界"的情景。
还需注意一个点:

对于本题,这两种写法写任意一个都可以。
二分查找的时间复杂度分析:

时间复杂度为logN的算法可比时间复杂度为N的厉害太多了。
1024个数据,时间复杂度为N的算法最多需要找1024次,时间复杂度为logN的算法最多只需要找10次。
1024*1024个数据(大约100万),时间复杂度为N的算法最多需要找100w次,时间复杂度为logN的算法最多只需要找20次。
二、在排序数组中查找元素的第一个和最后一个位置
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
给你一个按照非递减顺序排列的整数数组
nums,和一个目标值target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值
target,返回[-1, -1]。你必须设计并实现时间复杂度为
O(log n)的算法解决此问题。示例 1:
输入:nums = [5,7,7,8,8,10], target = 8 输出:[3,4]示例 2:
输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1]示例 3:
输入:nums = [], target = 0 输出:[-1,-1]提示:
0 <= nums.length <= 10^5-10^9 <= nums[i] <= 10^9nums是一个非递减数组-10^9 <= target <= 10^9
这道题的暴力解法是很好想出来的,遍历数组,首次遇到target记录它的下标,然后接着遍历记录最后一个值为target的下标,最后返回即可。
暴力解法代码实现:
//暴力解法:
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int n=nums.size();vector<int> ret;for(int i=0;i<n;i++){if(nums[i]==target)ret.push_back(i);}if(ret.empty())return {-1,-1};return {ret[0],ret[ret.size()-1]};}
};这道题可以直接用二分查找吗?
这道题可以用二分查找思想,但是不能直接套用第一题的模板样式,分析:

这道题为什么可以用二分思想呢?那么如何使用二分查找思想呢?
分析(以示例1为例):

别的一些细节,请大家在代码实现中仔细品味。
代码实现:
//二分思想
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {if(nums.empty())return {-1,-1};vector<int> ret;//1、二分左端点int left = 0,right=nums.size()-1; while(left < right){int mid = (right-left)/2 + left;if(nums[mid] < target)left = mid+1;elseright = mid;}if(nums[left] != target) return{-1,-1};ret.push_back(left);//2、二分右端点left = 0,right = nums.size()-1;while(left<right){int mid = (right-left+1)/2+left;if(nums[mid] > target)right = mid-1;elseleft = mid;}ret.push_back(right);return ret;}
};三、搜索插入位置
35. 搜索插入位置 - 力扣(LeetCode)
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为
O(log n)的算法。示例 1:
输入: nums = [1,3,5,6], target = 5 输出: 2示例 2:
输入: nums = [1,3,5,6], target = 2 输出: 1示例 3:
输入: nums = [1,3,5,6], target = 7 输出: 4提示:
1 <= nums.length <= 10^4-10^4 <= nums[i] <= 10^4nums为 无重复元素 的 升序 排列数组-10^4 <= target <= 10^4
这道题其实和第二题本质上是一样的,只是换一种形式和说法,就是第二题中求左端点的下标的问题。因为nums是无重复元素的升序排列数组,可以实现"分段",所以就是第二题的变形,我们直接上代码:
//二分思想
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(left < right){int mid = (right-left)/2+left;if(nums[mid] < target)left=mid+1;elseright=mid;}if(nums[right] < target) //处理特殊情况,应对示例3出现的情况return right+1;return right;}
};它的复杂度也符合题目中的O(logN)。
四、x 的平方根
69. x 的平方根 - 力扣(LeetCode)
给你一个非负整数
x,计算并返回x的 算术平方根 。由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如
pow(x, 0.5)或者x ** 0.5。示例 1:
输入:x = 4 输出:2示例 2:
输入:x = 8 输出:2 解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。提示:
0 <= x <= 2^31 - 1
这道题的暴力解法就是从1开始遍历看看哪个数的平方等于x,就返回,如果大于x,就返回一个数。
经过前面几个题的解题过程,这道题不就是第二道题中求右端点位置下标的变形嘛。想象数组中的元素从1到x,简直不要太一样了,直接上代码:
class Solution {
public:int mySqrt(int x) {int left = 1,right = x;while(left<right){long long mid = (right-left+1)/2+left; if(mid*mid > x) //为了防止溢出,mid的类型用long longright= mid-1;elseleft = mid;}return right;}
};
五、山脉数组的峰顶索引
852. 山脉数组的峰顶索引 - 力扣(LeetCode)
给定一个长度为
n的整数 山脉 数组arr,其中的值递增到一个 峰值元素 然后递减。返回峰值元素的下标。
你必须设计并实现时间复杂度为
O(log(n))的解决方案。示例 1:
输入:arr = [0,1,0] 输出:1示例 2:
输入:arr = [0,2,1,0] 输出:1示例 3:
输入:arr = [0,10,5,2] 输出:1提示:
3 <= arr.length <= 10^50 <= arr[i] <= 10^6- 题目数据 保证
arr是一个山脉数组
这道题用暴力解法就是从头遍历数组,如果当前数比后一个大,那么这个数就是峰值,返回其下标即可。
暴力解法代码:
class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int n = arr.size();// 遍历数组内每⼀个元素,直到找到峰顶for (int i = 1; i < n - 1; i++)// 峰顶满⾜的条件if (arr[i] > arr[i - 1] && arr[i] > arr[i + 1])return i;// 为了处理 oj 需要控制所有路径都有返回值return -1;}
};这道题中的数组是可以分段的,分析如下:

这道题的本质就是第二道题求左端点问题。
代码如下:
//二分思想
class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int n=arr.size();int left = 1,right=n-2; //峰顶不可能是第一个元素和最后一个元素while(left < right){int mid = (right-left)/2+left;if(arr[mid] < arr[mid+1])left = mid+1;elseright = mid;}return left;}
};时间复杂度满足O(logN)。
六、 寻找峰值
162. 寻找峰值 - 力扣(LeetCode)
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组
nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。你可以假设
nums[-1] = nums[n] = -∞。你必须实现时间复杂度为
O(log n)的算法来解决此问题。示例 1:
输入:nums = [1,2,3,1] 输出:2 解释:3 是峰值元素,你的函数应该返回其索引 2。示例 2:
输入:nums = [1,2,1,3,5,6,4] 输出:1 或 5 解释:你的函数可以返回索引 1,其峰值元素为 2;或者返回索引 5, 其峰值元素为 6。提示:
1 <= nums.length <= 1000-2^31 <= nums[i] <= 2^31 - 1- 对于所有有效的
i都有nums[i] != nums[i + 1]
经过题目描述,这道题会有以下几种情况:

我们可以将以上3中情况抽象为2种:

代码实现:
//二分思想
class Solution {
public:int findPeakElement(vector<int>& nums) {int n = nums.size();int left=0,right=n-1;while(left<right){int mid = (right-left)/2+left;if(nums[mid]<nums[mid+1])left = mid + 1;elseright = mid;}return left;}
};时间复杂度满足O(logN)。
五、六两题种数据并没有序,我们也能用二分查找思想解题,所以我们不要将二分思想局限到只能在有序数组中去运用。
七、寻找旋转排序数组中的最小值
153. 寻找旋转排序数组中的最小值 - 力扣(LeetCode)
已知一个长度为
n的数组,预先按照升序排列,经由1到n次 旋转 后,得到输入数组。例如,原数组nums = [0,1,2,4,5,6,7]在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2]- 若旋转
7次,则可以得到[0,1,2,4,5,6,7]注意,数组
[a[0], a[1], a[2], ..., a[n-1]]旋转一次 的结果为数组[a[n-1], a[0], a[1], a[2], ..., a[n-2]]。给你一个元素值 互不相同 的数组
nums,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。你必须设计一个时间复杂度为
O(log n)的算法解决此问题。示例 1:
输入:nums = [3,4,5,1,2] 输出:1 解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。示例 2:
输入:nums = [4,5,6,7,0,1,2] 输出:0 解释:原数组为 [0,1,2,4,5,6,7] ,旋转 3 次得到输入数组。示例 3:
输入:nums = [11,13,15,17] 输出:11 解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。提示:
n == nums.length1 <= n <= 5000-5000 <= nums[i] <= 5000nums中的所有整数 互不相同nums原来是一个升序排序的数组,并进行了1至n次旋转
这道题的暴力解法是遍历数组,如果当前值比下一个值大,就返回下一个元素;如果遍历完没有找到就返回第一个元素。暴力解法的时间复杂度是O(N)。
这道题很明显有分段情况,我们可以考虑用二分思想:

这道题本质上就是第二题中的求左端点问题。
代码实现:
//二分思想(以D为基准)
class Solution {
public:int findMin(vector<int>& nums) {int n=nums.size();int base = nums[n-1]; //以最后一个元素为基准值int left=0,right=n-1;while(left<right){int mid = (right-left)/2+left;if(nums[mid] > base)left=mid+1;elseright = mid;}return nums[left]; }
};以D为基准值,这段代码可以应对旋转后保持不变的情况。
我们也可以以A为基准值:
//二分思想(以A为基准)
class Solution {
public:int findMin(vector<int>& nums) {int n=nums.size();int base = nums[0]; //以第一个元素为基准值int left=0,right=n-1;while(left<right){int mid = (right-left)/2+left;if(nums[mid] < base)right=mid;elseleft = mid+1;}if(n == 1 || nums[left]>nums[left-1]) //处理旋转后保持不变的情况以及数组只有一个元素的情况return nums[0];return nums[left];}
};时间复杂度满足O(logN)。
八、点名
LCR 173. 点名 - 力扣(LeetCode)
某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组
records。假定仅有一位同学缺席,请返回他的学号。示例 1:
输入: records = [0,1,2,3,5] 输出: 4示例 2:
输入: records = [0, 1, 2, 3, 4, 5, 6, 8] 输出: 7提示:
1 <= records.length <= 10000
这个题的解题方法有很多:
1、异或法
开一个n个元素的数组,记录从0~n-1的所有值。新数组中所有数和records中所有元素异或,异或是"同0不1",所有异或后,剩下的那个值就是缺席同学的学号。
代码实现:
//异或法
class Solution {
public:int takeAttendance(vector<int>& records) {int ret=0; //记录最终结果int n = records.size()+1;vector<int> tmp(n); //新开的数组for(int i=0;i<n;i++)tmp.push_back(i);for(auto e: records)ret^=e;for(auto e:tmp)ret^=e;return ret;}
};代码还可以更简洁:
//异或法
class Solution {
public:int takeAttendance(vector<int>& records) {int ret=0;int n = records.size();for(int i=0;i <= n;i++){if(i < n)ret = ret ^ records[i] ^ i;elseret^=i;}return ret;}
};2、 数学法(高斯求和)
利用高斯求和公式求出0~n-1所有数的和然后减去records中所有元素相加的和,结果就是缺席同学的学号。
代码实现:
// 数学法(高斯求和)
class Solution {
public:int takeAttendance(vector<int>& records) {int n = records.size() + 1;int sum1 = ((0 + (n - 1)) * n) / 2; // 0~n-1的和int sum2 = 0; // recoeds中所有元素的和for (auto e : records)sum2 += e;return sum1 - sum2;}
};3、哈希思想
记录records中每个元素出现的次数,然后从0开始遍历,如果次数是0,就返回对应的数字。
代码实现:
//哈希映射
class Solution {
public:int takeAttendance(vector<int>& records) {int n = records.size()+1;unordered_map<int,int> hash; for(auto e:records)hash[e]++; //记录每个元素出现的次数for(int i=0;i<n;i++)if(hash[i]==0)return i; //缺失的数字return -1;}
};4、遍历法
//直接遍历法
class Solution {
public:int takeAttendance(vector<int>& records) {int n = records.size();int i=0;for(i=0;i<n;i++){if(records[i] != i)return i;}if(i == n) //处理数组是[0,1,2]类似这种的情况return i;return -1;}
};5、二分查找法
通过前面七道题的熏陶,这道题大家自己想如何用二分查找。
我在这里给出代码,大家可以参考一下:
//二分查找
class Solution {
public:int takeAttendance(vector<int>& records) {int left=0,right=records.size()-1;while(left < right){int mid = (right-left)/2+left;if(records[mid] == mid)left=mid+1;elseright=mid;}if(records[right] == right) //处理类似[0,1,2]这种数组的情况return right+1;return right;}
};相关文章:

【算法与数据结构】二分查找思想
#1024程序员节|征文# 正文: 二分查找(binary search)是一种基于分治策略的高效搜索算法。它利用数据的有序性,每轮缩小一半搜索范围,直至找到目标元素或搜索区间为空为止,其实有时候数据没有序…...

PHP PDO:安全、灵活的数据持久层解决方案
PHP PDO:安全、灵活的数据持久层解决方案 PHP PDO(PHP Data Objects)是一个轻量级的、具有兼容接口的数据持久层抽象层。它提供了一个统一的API来访问多种数据库系统,如MySQL、PostgreSQL、SQLite、Oracle等。PDO扩展在PHP 5.1.0…...

九、Linux实战案例:项目部署全流程深度解析
Linux实战案例:项目部署全流程深度解析 在当今信息技术领域,Linux服务器凭借其卓越的稳定性、安全性以及强大的性能表现,被广泛应用于各类项目部署场景之中。本文将全面深入地介绍如何将一个项目成功部署至Linux服务器的完整流程,…...
GIS常见前端开发框架
#1024程序员节|征文# 伴随GIS的发展,陆续出现了众多开源地图框架,这些地图框架与众多行业应用融合,极大地拓展了GIS的生命力,这里介绍几个常见的GIS前端开发框架,排名不分先后。 1.Leaflet https://leafl…...

Java | Leetcode Java题解之第506题相对名次
题目: 题解: class Solution {public String[] findRelativeRanks(int[] score) {int n score.length;String[] desc {"Gold Medal", "Silver Medal", "Bronze Medal"};int[][] arr new int[n][2];for (int i 0; i &…...

数据结构 - 堆
今天我们将学习新的数据结构-堆。 01定义 堆是一种特殊的二叉树,并且满足以下两个特性: (1)堆是一棵完全二叉树; (2)堆中任意一个节点元素值都小于等于(或大于等于)左…...

html----图片按钮,商品展示
源码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>图标</title><style>.box{width:…...

YOLOv11改进策略【卷积层】| ECCV-2024 小波卷积WTConv 增大感受野,降低参数量计算量,独家创新助力涨点
一、本文介绍 本文记录的是利用小波卷积WTConv模块优化YOLOv11的目标检测网络模型。WTConv的目的是在不出现过参数化的情况下有效地增加卷积的感受野,从而解决了CNN在感受野扩展中的参数膨胀问题。本文将其加入到深度可分离卷积中,有效降低模型参数量和计算量,并二次创新C3…...

redis高级篇之redis源码分析List类型quicklist底层演变 答疑159节
(1)ziplist压缩配置:list-compress-depth 0 表示一个quicklist两端不被压缩的节点个数。这里的节点是指quicklist双向链表的节点,而不是指ziplist里面的数据项个数参数list-compress-depth的取值含义如下: 0:是个特殊值,表示都不压缩。这是Redis的默认值…...

Elasticsearch 与 Lucene 的区别和联系
Elasticsearch 与 Lucene 的区别和联系 Elasticsearch 与 Lucene 的区别和联系一、知识背景Elasticsearch 简介Lucene 简介 二、Elasticsearch 和 Lucene 的区别适用场景性能优势和劣势架构设计的异同点 三、Elasticsearch和Lucene的联系四、Elasticsearch和Lucene的应用案例及…...

OpenCV视觉分析之运动分析(5)背景减除类BackgroundSubtractorMOG2的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 基于高斯混合模型的背景/前景分割算法。 该类实现了在文献[320]和[319]中描述的高斯混合模型背景减除。 cv::BackgroundSubtractorMOG2 类是 O…...

【SAP Hana】X-DOC:数据仓库ETL如何抽取SAP中的CDS视图数据
【SAP Hana】X-DOC:数据仓库ETL如何抽取SAP中的CDS视图数据 1、无参CDS对应数据库视图2、有参CDS对应数据库表函数3、封装有参CDS为无参CDS,从而对应数据库视图 1、无参CDS对应数据库视图 select * from ZFCML_REP_V where mandt 300;2、有参CDS对应数…...

WPF的UpdateSourceTrigger属性
在WPF中,UpdateSourceTrigger属性用于控制数据绑定中何时将绑定目标(通常是UI元素)的值更新回绑定源(通常是数据对象)。这个属性有以下几个值: Default:这是默认值,对于不同的绑定目…...

2024-09-25 环境变量,进程地址空间
一、认识常见的环境变量 1. echo $HOME 输出当前用户对应的家目录 当用户登录系统时,流程如下: (1)用户登录系统后,系统启动Shell程序。 (2)启动bash shell,准备接收用户指令。 &a…...

中国移动机器人将投入养老场景;华为与APUS共筑AI医疗多场景应用
AgeTech News 一周行业大事件 华为与APUS合作,共筑AI医疗多场景应用 中国移动展出人形机器人,预计投入养老等场景 作为科技与奥富能签约,共拓智能适老化改造领域 天与养老与香港科技园,共探智慧养老新模式 中山大学合作中国…...
)
青少年编程能力等级测评CPA C++ 四级试卷(1)
青少年编程能力等级测评CPA C 四级试卷(1) 一、单项选择题(共15题,每题3分,共45分) CP4_1_1.在面向对象程序设计中,与数据构成一个相互依存的整体的是( )。 A. 对数据…...

树上任意两点的距离
题目描述 给出 n 个点的一棵树,多次询问两点之间的最短距离。 注意:边是双向的。 输入描述 第一行为两个整数 n 和 m。n 表示点数,m 表示询问次数; 下来 n−1 行,每行三个整数 x,y,k,表示点 x 和点 y 之间…...

【 thinkphp8 】00008 thinkphp8数据查询,常用table,name方法,进行数据查询汇总
前言:哈喽,大家好,今天给大家分享一篇文章!并提供具体代码帮助大家深入理解,彻底掌握!创作不易,如果能帮助到大家或者给大家一些灵感和启发,欢迎收藏关注哦 💕 目录 【 t…...

Git的命令合集
关于Git的一些命令合集,会慢慢更新! 20241024程序员节开始写的,记录一下~~ git查看log、查看详细提交记录 会显示之前的提交记录 , 排序由近及远 git log log按q退出 git回退到某个commit命令: 退到/进到指定commit的sha码&…...
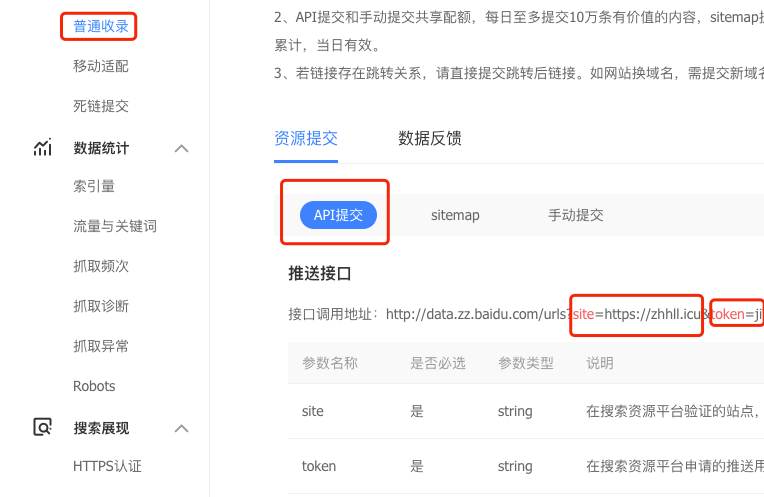
博客搭建之路:hexo搜索引擎收录
文章目录 hexo搜索引擎收录以百度为例 hexo搜索引擎收录 hexo版本5.0.2 npm版本6.14.7 next版本7.8.0 写博客的目的肯定不是就只有自己能看到,想让更多的人看到就需要可以让搜索引擎来收录对应的文章。hexo支持生成站点地图sitemap 在hexo下的_config.yml中配置站点…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
