反向传播的微积分原理 | Chapter 4 | Deep Learning | 3Blue1Brown
目录
- 前言
- 1. 简介
- 2. 神经网络中的链式法则
- 3. 微积分的计算
- 4. 公式含义
- 5. 代价函数对权重偏置的敏感度
- 6. 多个神经元的情形
- 7. 回顾
- 相关资料
- 结语
前言
3Blue1Brown 视频笔记,仅供自己参考
这个章节主要来深度讲解反向传播中的一些微积分理论
官网:https://www.3blue1brown.com
视频:https://www.bilibili.com/video/BV16x411V7Qg
1. 简介

这章开始我们就假设你已经看过第三章了,上章让大家直观上感受了反向传播算法的原理

在这章里,我们会更深入讲解一些其中的微积分理论,这个看不太懂很正常,所以我们的六字格言 “停一停想一想” 在这依旧管用,这章我们的目标是给大家展示在机器学习中,我们一般是怎么理解链式法则的,这点跟别的基础微积分课讲得会有点不一样

对于微积分不够熟悉的观众,我之前已经做了一整个系列了,大家感兴趣的可以看看:Calculus
2. 神经网络中的链式法则

我们从最最简单的网络讲起吧,每层只有一个神经元

图上这个网络就是由 3 个权重和 3 个偏置决定的,我们的目标是理解代价函数对于这些变量有多敏感,这样我们就知道怎么调整这些变量才可以使得代价降低得最快,

我们先来关注最后两个神经元吧,我给最后一个神经元的激活值一个上标 L,表示它处于第 L 层,那么,前一个神经元的激活值就是 a ( L − 1 ) a^{(L-1)} a(L−1),这里的上标不是指数,而是用来标记我们正在讨论哪一层,过一会我会用到下标来表示别的意思

给定一个训练样本,我们把这个最终层激活值要接近的目标叫做 y,例如 y 可能是 0 或者 1,那么这个简易网络对于单个训练样本的代价就等于 ( a ( L ) − y ) 2 \color{black}(a^{(L)}-\color{gold}y\color{black})^2 (a(L)−y)2,对于这个样本,我们把这个代价值标记为 C 0 \color{red}C_0 C0

还记得吗,最终层的激活值是这么算出来的,即一个权重 w L \color{blue}w^L wL 乘上前一个神经元的激活值再加上一个偏置 b L \color{pink}b^L bL,最后把加权和塞进一个特定的非线性函数,例如 sigmoid 或者 ReLU 之类的,给这个加权和起一个名字会方便很多,就叫它 z L \color{green}z^L zL 好了,跟对应的激活值用同一个上标

这里的项挺多,概括起来我们拿权重 w L \color{blue}w^L wL、前一个激活值 a ( L − 1 ) a^{(L-1)} a(L−1) 以及偏置值 b L \color{pink}b^L bL 一起来算出 z L \color{green}z^L zL 再算出 a ( L ) a^{(L)} a(L),最后再用上常量 y \color{gold}y y 算出代价值 C 0 \color{red}C_0 C0,当然 a ( L − 1 ) a^{(L-1)} a(L−1) 也是由它自己的权重和偏置决定的,以此类推,但我们现在重点不在那里

上面这些东西都是数字,没错吧,我们可以想象每个数字都对应一个数轴,我们第一个目标是理解代价函数对权重 w L \color{blue}w^L wL 的微小变化有多敏感,或者换句话讲求 C 0 \color{red}C_0 C0 对 w L \color{blue}w^L wL 的导数

当你看到 ∂ w \color{blue}\partial w ∂w 之类的项时,请把它当做这是对 w \color{blue}w w 的微小扰动,好比改变 0.01,然后把 ∂ C 0 \color{red}\partial C_0 ∂C0 当做 “改变 w \color{blue}w w 对 C 0 \color{red}C_0 C0 的值造成的变化”,我们求得是这两个数的比值

概念上说 w L \color{blue}w^L wL 的微小变化会导致 z L \color{green}z^L zL 产生些变化,然后会导致 a L a^L aL 产生变化,最终影响到代价值

那么,我们把式子拆开,首先求 z L \color{green}z^L zL 的变化量比上 w L \color{blue}w^L wL 的变化量,也就是求 z L \color{green}z^L zL 关于 w L \color{blue}w^L wL 的导数,同理考虑 a L a^L aL 的变化量比上因变量 z L \color{green}z^L zL 的变化量,以及最终的 C 0 \color{red}C_0 C0 的变化量比上直接改动 a L a^L aL 产生的变化量

这不就是链式法则么,把三个比值相乘就可以算出 C 0 \color{red}C_0 C0 对 w L \color{blue}w^L wL 的微小变化有多敏感
3. 微积分的计算

现在图上多了一大堆符号,稍微花点时间理解一下每个符号都是什么意思吧,因为马上我们就要对各个部分求导了

C 0 \color{red}C_0 C0 关于 a L a^L aL 的导数就是 2 ( a ( L ) − y ) \color{black}2(a^{(L)}-\color{gold}y\color{black}) 2(a(L)−y),这也就意味着导数的大小跟网络最终的输出减目标结果的差成正比,如果网络的输出差别很大,即使 w \color{blue}w w 稍稍变一点代价也会改变非常大

a L a^L aL 对 z L \color{green}z^L zL 求导就是求 sigmoid 的导数,或就你选择的非线性激活函数求导

而 z L \color{green}z^L zL 对 w L \color{blue}w^L wL 求导结果就是 a L − 1 a^{L-1} aL−1
4. 公式含义

对我自己来说,这里如果不退一步好好想想这些公式的含义,很容易卡住

就最后这个导数来说,这个权重的改变量 ∂ w \color{blue}\partial w ∂w 对最后一层的影响有多大取决于之前一层的神经元,所谓的 “一同激活的神经元关联在一起” 的出处即来源于此

不过这只是包含一个训练样本的代价对 w ( L ) \color{blue}w^{(L)} w(L) 的导数,由于总的代价函数是许许多多训练样本所有代价的总平均,它对 w ( L ) \color{blue}w^{(L)} w(L) 的导数就需要求 ∂ C ∂ w ( L ) \frac{\color{red}\partial C}{\color{blue}\partial w^ {(L)}} ∂w(L)∂C 这个表达式之于每一个训练样本的平均

当然这只是梯度向量 ∇ C \color{red}\nabla C ∇C 的一个分量,而梯度向量 ∇ C \color{red}\nabla C ∇C 本身则由代价函数对每一个权重和每一个偏置求偏导构成的
5. 代价函数对权重偏置的敏感度


值得注意的是,求出这些偏导中的一个就完成了一大半的工作量,对偏置的求导步骤也就基本相同,只要把 ∂ z ∂ w \frac{\color{green}\partial z}{\color{blue} \partial w} ∂w∂z 替换成 ∂ z ∂ b \frac{\color{green}\partial z}{\color{pink} \partial b} ∂b∂z,对应的公式中可以看出导数 ∂ z ∂ b \frac{\color{green}\partial z}{\color{pink} \partial b} ∂b∂z 等于 1

这里也涉及到了反向传播的概念,我们来看下这个代价函数对上一层激活值的敏感度,展开来说,链式法则的第一项 z \color{green}z z 对上一层激活值的敏感度就是权重 w ( L ) \color{blue}w^{(L)} w(L)

虽然说过我们不能直接改变激活值,但我们很有必要关注这个值,因为我们可以反向应用链式法则来计算代价函数对之前的权重偏置的敏感度
6. 多个神经元的情形

你可能觉得这个例子举得太简单了,毕竟每层只有一个神经元,而真实的神经网络会比这个例子复杂百倍,然而说真的,每层多加若干个神经元并不会复杂很多,真的,只不过多写一些下标罢了

我们用加上下标的神经元来表示 L 层的若干神经元,而不是用 a ( L ) a^{(L)} a(L) 统称 L 层的激活值,现在用 k 来标注 L-1 层的神经元,j 则是 L 层的神经元

现在要求代价函数,我们从期望的输出着手,计算上一层激活值和期望输出的差值的平方然后求和,即求 ( a j ( L ) − y j ) 2 \color{black}(a_j^{(L)}-\color{gold}y_j\color{black})^2 (aj(L)−yj)2 的和

由于权重的数量多了不少,那么每个权重要多用几个下标,我们记连接第 k 个神经元和第 j 个神经元的连线为 w j k ( L ) \color{blue}w_{jk}^{(L)} wjk(L),这些下标感觉像标反了,可能有点别扭,不过和第一章中的权重矩阵的下标是一致的

同样的,把加权和记为 z 总是很方便,那么最后一层的激活值依然等于指定的函数(如 sigmoid)在 z 处的函数值


你懂我意思吧,现在的方程式和之前每层只有一个神经元的时候本质是一样的,只是看着复杂一些

链式法则形式的导数表达式所描述的代价对某个权重的敏感度也是一样的,这里大家可以暂停推导一下每一项的含义,唯一改变的是代价对 L-1 层激活值的导数

此时,激活值可以通过不同的途径影响代价函数,也就是说,神经元一边通过 a 0 ( L ) a_0^{(L)} a0(L) 来影响代价函数,另一边通过 a 1 ( L ) a_1^{(L)} a1(L) 来影响代价函数,得把这些都加起来,然后…就搞定了

只要计算出倒数第二层代价函数对激活值的敏感度,接下来只要重复上述过程,计算喂给倒数第二层的权重和偏置就好了
7. 回顾
现在长吁一口气吧!如果上面这些明白了,那你就看明白了神经网络的主力—反向传播

链式法则表达式给出了决定梯度每个分量的偏导,使得我们能不断下探,最小化神经网络的代价

静下来想一想你会发现这些复杂的层层叠叠很烧脑,消化这些知识需要花一些时间,这很正常
相关资料
- http://neuralnetworksanddeeplearning.com/chap2.html
- https://github.com/mnielsen/neural-networks-and-deep-learning
- https://colah.github.io/posts/2015-08-Backprop/
结语
这个章节我们主要学习了反向传播以微积分的形式表达,其核心就是链式法则
OK,以上就是本章的全部内容了,下章我们来讲 Transformer,敬请期待😄
相关文章:

反向传播的微积分原理 | Chapter 4 | Deep Learning | 3Blue1Brown
目录 前言1. 简介2. 神经网络中的链式法则3. 微积分的计算4. 公式含义5. 代价函数对权重偏置的敏感度6. 多个神经元的情形7. 回顾相关资料结语 前言 3Blue1Brown 视频笔记,仅供自己参考 这个章节主要来深度讲解反向传播中的一些微积分理论 官网:https://…...

matlab读取excel表格
使用matlab读取excel表格中的数据 使用推荐代码读取excel表格中的数据 path "C:\Users\24975\Desktop\503\GUI展示案例\Tx_20_0_Rx_40_90_0.1_95_L.xlsx";%文件路径 data readtable(path,Sheet,Sheet1,ReadRowNames,false,ReadVariableNames,false,Ra…...

基于springboot+vue实现的助学兼职系统(源码+L文+ppt)4-092
基于springbootvue实现的助学兼职系统(源码L文ppt)4-092 第4章 系统设计 4.1 总体功能设计 一般学生、招聘公司和管理者都需要登录才能进入助学兼职系统,使用者登录时会在后台判断使用的权限类型,包括一般使用者和管理者,一般使…...

⌈ 传知代码 ⌋ 农作物病害分类(Web端实现)
💛前情提要💛 本文是传知代码平台中的相关前沿知识与技术的分享~ 接下来我们即将进入一个全新的空间,对技术有一个全新的视角~ 本文所涉及所有资源均在传知代码平台可获取 以下的内容一定会让你对AI 赋能时代有一个颠覆性的认识哦&#x…...

CMU生成式人工智能大模型:从入门到放弃(九)
引言 在前面的系列博客中,我们深入探讨了生成式对抗网络(GANs)和变分自编码器(VAEs)等生成式模型。今天,我们将探索扩散模型(Diffusion Models)的进一步应用,并讨论在上…...

HTML基础总结
一、简介 HTML(HyperText Markup Language)即超文本标记语言,是用于创建网页的标准标记语言。它通过使用各种标签来定义网页的结构和内容,告诉浏览器如何显示网页。HTML 文档由标签和文本组成,标签用于描述文本的性质…...
EXCELL中如何两条线画入一张图中,标记坐标轴标题?
1,打开excel,左击选中两列, 2,菜单栏>“插入”>”二维折线图”选中一个 3,选中出现的两条线中的一条右击>最下一行,“设置数据系列格式” 4,右测“系列选项中”>点击“次坐标轴” 5…...

Zabbix企业级分布式监控环境部署
“运筹帷幄之中,决胜千里之外”。在IT运维中,监控占据着重要的地位,按比例来算,说占30%一点也不为过。对IT运维工程师来说,构建一个真正可用的监控告警系统是一项艰巨的任务。在监控系统的开源软件中,可供选…...

水轮发电机油压自动化控制系统解决方案介绍
在现代水电工程中,水轮机组油压自动化控制系统,不仅直接关系到水轮发电机组的安全稳定运行,还影响着整个水电站的生产效率和经济效益。 一、系统概述 国科JSF油压自动控制系统,适用于水轮发电机组调速器油压及主阀(蝶…...

今天不分享技术,分享秋天的故事
引言 这个爱情故事好像是个悲剧,你说的是婚姻。爱情没有悲剧,对爱者而言,爱情怎么会是悲剧呢。对春天而言,秋天是它的悲剧吗。结尾是什么,等待,之后呢,没有之后。或者说,等待的结果…...

转录组上游分析流程(三)
环境部署——数据下载——查看数据(非质控)——数据质控——数据过滤(过滤低质量数据) 测序得到的原始序列含有接头序列和低质量序列,为了保证信息分析的准确性,需要对原始数据进行质量控制,得到高质量序列(Clean Reads),原始序列…...

excel判断某一列(A列)中的数据是否在另一列(B列)中
如B列如果有7个元素,在A列右边的空白列中,输入如下公式: COUNTIF($B$1:$B$7,A1), 其中,$B$1:$B$7代表A列中的所有数据即绝对范围,A1代表B列中的一个单元格....

[环境配置]macOS上怎么查看vscode的commit id
macOS的commit id和windows上有点不一样,windows可以在帮助-关于查看 macOS则需要再左边第一个查看...
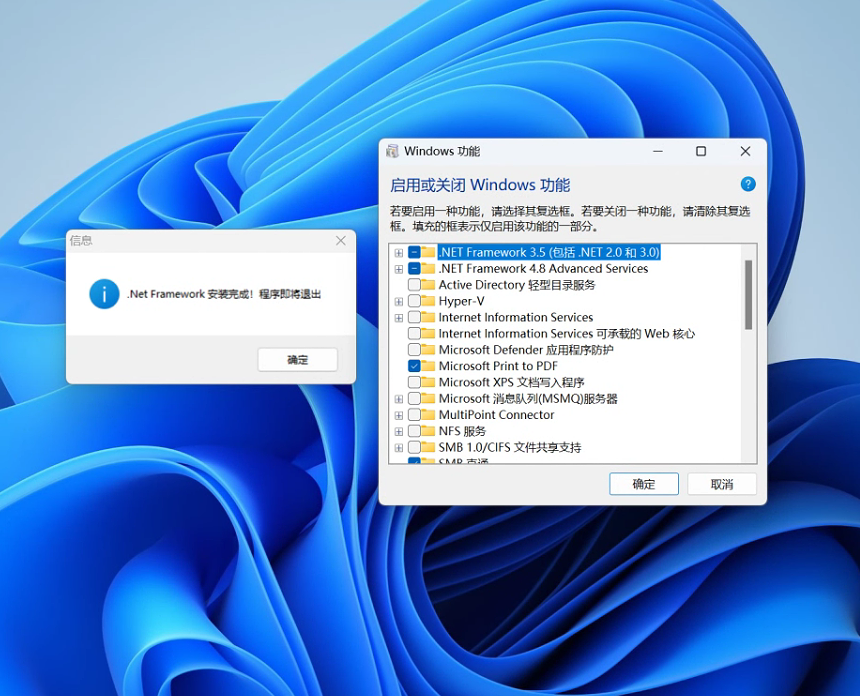
.net framework 3.5sp1组件安装进度条不动启动错误怎么解决
安装.NET Framework 3.5 SP1通常需要管理员权限。这是因为安装过程可能需要修改系统文件和注册表项,这些操作通常需要管理员权限才能执行。在Windows系统上,安装.NET Framework 3.5 SP1通常通过控制面板中的“启用或关闭Windows功能”选项进行࿰…...

学习threejs,利用THREE.ExtrudeGeometry拉伸几何体实现svg的拉伸
👨⚕️ 主页: gis分享者 👨⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨⚕️ 收录于专栏:threejs gis工程师 文章目录 一、🍀前言1.1 ☘️THREE.ExtrudeGeometry拉伸…...

大模型之三十二-语音合成TTS(coqui) 之二 fine-tune
在 大模型之三十-语音合成TTS(coqui)[shichaog CSDN]中提到了xttsv2的fine-tune。 数据情况: 我是从bilibili up主小Lin说提取了一些视频,然后进行了重新的fine-tune。 训练结果 如下图所示,上面波形幅度较大的是xttsv2原始模型的结果&am…...
)
JVM的内存模型是什么,每个区域的作用是什么,以及面试题(含答案)
JVM(Java 虚拟机)内存模型定义了 Java 程序在运行时如何分配、管理和优化内存。JVM 内存模型主要分为几个关键区域,每个区域有特定的作用: JVM 内存模型 堆内存(Heap): 作用:用于存…...

《设计模式三》Java代理模式实现
Java代理模式实现 静态代理实现 // Subject.java // 主题接口,定义了请求方法 public interface Subject {void request(); }// RealSubject.java // 真实主题实现类,实现了Subject接口 public class RealSubject implements Subject {Overridepublic …...

vue3中计算属性的用法以及使用场景
在 Vue 3 中,计算属性(computed properties)是一种基于依赖项动态计算并缓存的响应式数据。它与 Vue 2 中的计算属性类似,但在组合式 API 中使用 computed 函数来定义。计算属性的核心优势在于能够自动缓存计算结果,仅…...

pytorh学习笔记——cifar10(六)MobileNet V1网络结构
基础知识储备: 一、深度可分离卷积(Depthwise Separable Convolution) MobileNet的核心是深度可分离卷积(Depthwise Separable Convolution),深度可分离卷积是卷积神经网络(CNN…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
