【小白学机器学习24】 用例子来比较:无偏估计和有偏估计
目录
1 关于无偏估计
1.1 无偏估计的定义
2 原始数据
2.1 假设我们是上帝,我们能创造一个总体/母体 population
2.2 按尽量随机取样的原则去取1个随机样本 sample1
3 一个关于无偏估计的理解
3.1 接着上面的总体和样本 sample1
3.2 左边的计算,期望是有偏的
3.3 右边的计算,期望是无偏的
3.4 差别和原因:
3.5 反思
4 思考:应该有其他办法保证 样本的均值无偏
4.1最大似然估计法:
4.2 样本方差 与无偏估计
1 关于无偏估计
1.1 无偏估计的定义
- 估计量的数学期望等于被估计参数的真实值,则称此估计量为被估计参数的无偏估计,即具有无偏性
无偏估计是用样本统计量来估计总体参数时的一种无偏推断。估计量的数学期望等于被估计参数的真实值,则称此估计量为被估计参数的无偏估计,即具有无偏性,是一种用于评价估计量优良性的准则。无偏估计的意义是:在多次重复下,它们的平均数接近所估计的参数真值。无偏估计常被应用于测验分数统计中。

下面是我自己搞的一个简单推理过程
2 原始数据
2.1 假设我们是上帝,我们能创造一个总体/母体 population
设计一个总体:在min~ max 产生一堆随机值
具体落地:
- 设计一个只包含int的整体。
- 在excel用公式RANDBETWEEN(E$1,E$2), min=10,max=20 生成了2000个数,作为总体
- 其中 mean=14.8805
- 注意EXCEL的随机公式每次保存都重算,所以先粘贴一列随机数保持不变。

2.2 按尽量随机取样的原则去取1个随机样本 sample1
随机取样,需要每个元素有平等的机会,而不是随便取样!
随机取样方法
- 样本的取法1:从总体里按等距的方法,取10个序号,拿出对应的数字,INDEX(B:B,MATCH(N4,A:A,0))
- 样本的取法2:从总体里取10个出来,random(1,2000) 序号应该也可以
- 样本的取法3: 写一个min max随机的单独的函数, 好像也可以吧,不过像是从更理想的总体,10-20均匀分布的总体里取得,我这个2000个数据得总体,每个整数必然不是完全等概率分布得
错误方法
- 随便取前10个数,这样的。。。。
3 一个关于无偏估计的理解
3.1 接着上面的总体和样本 sample1
- 取所有可能的数值(基本事件)
- 要计算期望/平均值,就需要知道概率
- 概率的计算有2种方式
- 方式1:一般我们不知道整体,只能假设整体是平均分布的,按等概率算
- 方式2:假设我们知道总体情况, 按我设计的2000个总体里不同数字出现的真实频度,作为真实的概率

3.2 左边的计算,期望是有偏的
- 计算期望
- 取每个基本事件:每个可能出现的数字int
- 一般我们不知道整体,只能假设整体是平均分布的,按等概率算,得到样本期望15
- 但是总体期望14.8805,两者有差异
3.3 右边的计算,期望是无偏的
- 计算期望
- 取每个基本事件:每个可能出现的数字int
- 假设我们知道总体情况, 按我设计的2000个总体里不同数字出现的真实频度,作为真实的概率,得到样本期望14.8805
- 但是总体期望14.8805,两者一样,无偏
3.4 差别和原因:
- 这样看来,无偏估计是很难的,需要知道真实的整体。
- 但是我这里的例子特殊,因为,样本是我这个假装的上帝设计的。并不是真正的现实中,那种不可完全认识的总体!
- 所以无偏估计,就要求,能完全模拟整体,越像整体,估计越是无偏的!
3.5 反思
- 但是一般情况下,我们假设真实的整体符合概率规律,如等概率更科学,比例子里的2000整体更科学。因为现实里我们永远不知道真实的总体到底多大,具体的概率分布细节。只可能知道样本的情况。这个有点上帝视角了。
- 如果知道了总体(即使是人为,人造的命题,比如本例),就用总体的概率, 分布去计算,样本的误差才会无偏
4 思考:应该有其他办法保证 样本的均值无偏
4.1最大似然估计法:
- 最大似然估计法是基于似然函数的性质来求解无偏估计量的。
- 似然函数是指在给定样本的情况下,总体参数取某个特定值时的概率密度函数。
- 最大似然估计法的基本思想是:在所有可能的总体参数值中,选择使得似然函数值最大的那个值作为总体参数的估计值
网上搜了下没看懂

4.2 样本方差 与无偏估计
样本方差要 /(n-1) 而不是/n ,就是为了获得无偏估计

- 主要取决于我们是否知道总体均数
- 如果知道总体均数,那么就除以n;
- 如果不知道总体均数,而只能用样本均数代替,那么就除以n-1。
Pearson相关系数
- Pearson相关系数是用来衡量两个变量之间线性相关程度的统计量。
- X和Y是两个变量,ρ是相关系数,cov是协方差,σ是标准差:

相关文章:

【小白学机器学习24】 用例子来比较:无偏估计和有偏估计
目录 1 关于无偏估计 1.1 无偏估计的定义 2 原始数据 2.1 假设我们是上帝,我们能创造一个总体/母体 population 2.2 按尽量随机取样的原则去取1个随机样本 sample1 3 一个关于无偏估计的理解 3.1 接着上面的总体和样本 sample1 3.2 左边的计算,期…...

C++在实际项目中的应用第二节:C++与网络编程
第五章:C在实际项目中的应用 第二节:C与网络编程 1. TCP/IP协议详解与C实现 TCP/IP(传输控制协议/互联网协议)是现代互联网通信的基础协议。理解 TCP/IP 协议对于开发网络应用至关重要。本节将详细介绍 TCP/IP 协议的工作原理以…...

依赖关系是危险的
依赖, 我们需要它们,但如何有效安全地使用它们?在本周的节目中,Kris 与 Ian 和 Johnny 一起讨论了 polyfill.io 供应链攻击、Go 中依赖管理和使用的历史,以及 Go 谚语“一点复制胜过一点依赖”。当然,我们用一些不受欢…...

ipguard与Ping32如何加密数据防止泄露?让企业信息更安全
在信息化时代,数据安全已成为企业运营的重中之重。数据泄露不仅会导致经济损失,还可能损害企业声誉。因此,选择合适的数据加密工具是保护企业敏感信息的关键。本文将对IPGuard与Ping32这两款加密软件进行探讨,了解它们如何有效加密…...

gitlab 的备份与回复
一、gitlab备份 1.确定备份目录 gitlab 默认的备份目录为/var/opt/gitlab/backups,可通过配置gitlab.rb配置文件进行修改,如: [rootlocalhost ~]# vim /etc/gitlab/gitlab.rb #若要修改备份文件的存储目录话,打开下面选项的注释…...

创建型模式-----建造者模式
目录 背景: 构建模式UML 代码示例 房子成品: 构建器抽象: 具体构建器: 建筑师: 测试部…...

威胁 Windows 和 Linux 系统的新型跨平台勒索软件:Cicada3301
近年来,网络犯罪世界出现了新的、日益复杂的威胁,能够影响广泛的目标。 这一领域最令人担忧的新功能之一是Cicada3301勒索软件,最近由几位网络安全专家进行了分析。他们有机会采访了这一危险威胁背后的勒索软件团伙的成员。 Cicada3301的崛…...

Go 语言基础教程:7.Switch 语句
在这篇教程中,我们将学习 Go 语言中的 switch 语句,它是条件分支的重要结构。我们将通过一个示例程序逐步解析 switch 的不同用法。 package mainimport ("fmt""time" )func main() {i : 2fmt.Print("Write ", i, " …...

mysql原理、部署mysql主从+读写分离、监控mysql主从脚本
mysql:工作原理 从库生成两个线程,一个I/O线程,一个SQL线程; i/o线程去请求主库 的binlog,并将得到的binlog日志写到relay log(中继日志) 文件中; 主库会生成一个 log dump 线程&…...
模型选择拟合
1.通过多项式拟合交互探索概念 import math import numpy as np import torch from torch import nn from d2l import torch as d2l 2.使用三阶多项式来生成训练和测试数据的标签 max_degree 20 # 多项式的最大阶数 n_train, n_test 100, 100 # 训练和测试数据集大小 true…...

文案语音图片视频管理分析系统-视频矩阵
文案语音图片视频管理分析系统-视频矩阵 1.产品介绍 产品介绍方案 产品名称: 智驭视频矩阵深度分析系统(SmartVMatrix) 主要功能: 深度学习驱动的视频内容分析多源视频整合与智能分类高效视频检索与编辑实时视频监控与异常预警…...
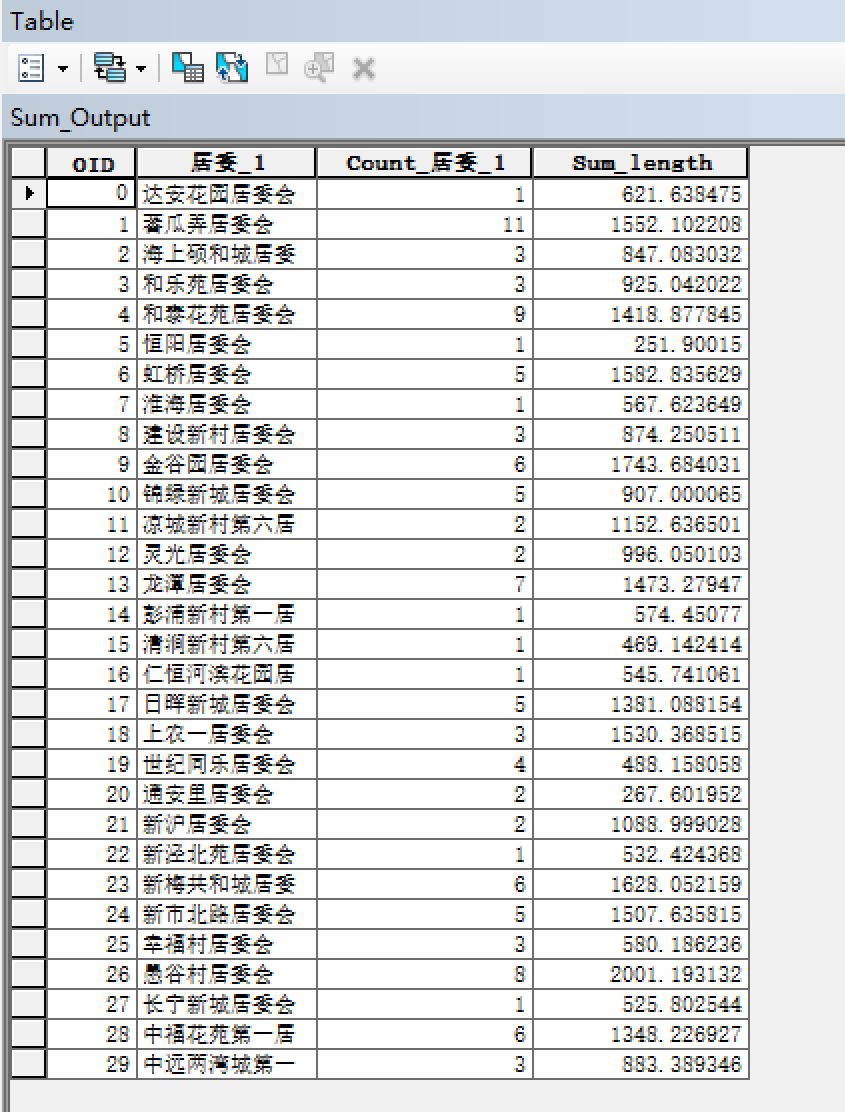
ArcGIS计算落入面图层中的线的长度或面的面积
本文介绍在ArcMap软件中,计算落入某个指定矢量面图层中的另一个线图层的长度、面图层的面积等指标的方法。 如下图所示,现在有2个矢量要素集,其中一个为面要素,表示某些区域;另一个为线要素,表示道路路网。…...

ctfshow-web入门-web172
//拼接sql语句查找指定ID用户 $sql "select username,password from ctfshow_user2 where username !flag and id ".$_GET[id]." limit 1;"; 联合查询 该题目与上一个题目不是同一个类型,该题目需要进行sql联合查询。 第一步:确…...

Keep健身TV版 3.3.0 | 针对智能电视的健身塑形软件
Keep健身TV版是专为智能电视设计的功能强大的健身塑形软件。该软件根据用户的不同需求提供多种器械和阶段健身目标组合编排,为用户提供科学、规范、专业的实时指导。即便是在家没有健身器械的情况下,也能跟随教练的语音指导一步步完成训练。软件涵盖从有…...

推荐一些关于计算机网络和 TCP/IP 协议的书籍
以下是一些关于计算机网络和 TCP/IP 协议的优秀书籍推荐: 《TCP/IP 详解》: 作者为 W.Richard Stevens,这是一套经典之作,分为三卷。《TCP/IP 详解卷 1:协议》:详细解析了 TCP/IP 协议的工作原理和实现细节,对协议族中的各个层次和协议,如 IP、TCP、UDP 等进行了深入剖…...

生成式AI浪潮下的商业机遇与经济展望 —— 与互联网时代的比较
一、引言 近年来,生成式人工智能(AI)技术迅速崛起,不仅吸引了大量资本的关注,同时也催生了诸多创新商业模式。与互联网早期阶段类似,AI领域同样面临着前所未有的发展机遇。本文将探讨生成式AI与互联网时代的异同,并分析当前AI行业的经济状况及其增长潜力。 二、经济形…...

Go 标准库
本篇内容是根据2016年9月份The Go Standard Library音频录制内容的整理与翻译, BoltDB 的创建者 Ben Johnson 参加了节目,讨论 NoSQL 与 SQL 数据库、两者之间的权衡以及选择其中之一。我们还讨论了 Ben 的数据秘密生活项目,可视化数据结构,…...

AUTOSAR_EXP_ARAComAPI的6章笔记(5)
☞返回总目录 相关总结:AUTOSAR 通信组的使用方法总结 6.5 通信组的使用方法 6.5.1. 设置 本节描述了使用 Communication Group Template(类别为 COMMUNICATION_GROUP)定义通信组的配置步骤。定义一个通信组需要指定三个项目:…...

Photoshop中的混合模式公式详解
图层混合简介 图层混合(blend)顾名思义,就是把两个图层混合成一个。 最基本的混合是alpha融合(alpha compositing),这是一个遵循光的反射与透射等(简化版)物理学原理的混合方式。 各…...

Vue 自定义指令 Directive 的高级使用与最佳实践
前言 Vue.js 是一个非常流行的前端框架,它的核心理念是通过声明式的方式来描述 UI 和数据绑定。除了模板语法和组件系统,Vue 还提供了一个强大的功能——自定义指令。 自定义指令可以让我们对 DOM 元素进行底层操作,下面让我们通过一个有趣的…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
