回溯算法-Java【力扣】【算法学习day.14】
前言
###我做这类文档一个重要的目的还是给正在学习的大家提供方向(例如想要掌握基础用法,该刷哪些题?)我的解析也不会做的非常详细,只会提供思路和一些关键点,力扣上的大佬们的题解质量是非常非常高滴!!!
什么是回溯算法
回溯搜索法是一种搜索方式,它通过不断尝试各种可能的选择,当发现当前选择不满足条件时,就回溯到上一个状态,重新进行选择,直到找到满足条件的解或者遍历完所有可能的情况。例如在解决迷宫问题时,可以使用回溯搜索法,从一个起始位置开始尝试不同的方向前进,如果遇到死路就回溯到上一个位置,重新选择其他方向。
习题
1.组合
题目链接:77. 组合 - 力扣(LeetCode)
题面:
基本分析:抽象成树的结构进行递归
代码:
class Solution {int len;public List<List<Integer>> combine(int n, int k) {List<List<Integer>> ans = new ArrayList<>();Stack<Integer> stack = new Stack<>();len = k;recursion(1,n,ans,stack);return ans;}public void recursion(int start,int end,List<List<Integer>> ans,Stack<Integer> stack){if(stack.size()==len){ans.add(new ArrayList<>(stack));return;}for(int i = start;i<=end - (len - stack.size()) + 1;i++){stack.push(i);recursion(i+1,end,ans,stack);stack.pop();}}
}2.组合总和III
题目链接:216. 组合总和 III - 力扣(LeetCode)
题面:
基本分析:和上一题类似,只不过多一个判断相加之和
代码:
class Solution {int len;int target;public List<List<Integer>> combinationSum3(int k, int n) {List<List<Integer>> ans = new ArrayList<>();len = k;target = n;Stack<Integer> stack = new Stack<>();recursion(1,9,stack,ans,0);return ans;}public void recursion(int l,int r,Stack<Integer> stack,List<List<Integer>> ans,int sum){if(sum>target)return;if(stack.size()>len)return;if(sum==target&&stack.size()==len)ans.add(new ArrayList<>(stack));for(int i = l;i<=r-(len-stack.size())+1;i++){stack.push(i);recursion(i+1,r,stack,ans,sum+i);stack.pop();}}
}3.电话号码的字母组合
题目链接:17. 电话号码的字母组合 - 力扣(LeetCode)
题面:
基本分析:暴力递归
代码:
class Solution {char[][] arr = {{'d'},{'a'},{'a','b','c'},{'d','e','f'},{'g','h','i'},{'j','k','l'},{'m','n','o'},{'p','q','r','s'},{'t','u','v'},{'w','x','y','z'}};int count = -1;int len;public List<String> letterCombinations(String digits) {List<String> list = new ArrayList<>();if(digits.equals(""))return list; char[] brr = digits.toCharArray();int n = brr.length;len = n;char[] crr = new char[n];recursion(0,brr,crr,list);return list;}public void recursion(int u,char[] brr,char[] crr,List<String> list){if(u==len){list.add(new String(crr));return;}char c = brr[u];char[] drr = arr[c-'0'];int m = drr.length;for(int i = 0;i<m;i++){crr[++count]=drr[i];recursion(u+1,brr,crr,list);count--;}}
}4.组合总和
题目链接:39. 组合总和 - 力扣(LeetCode)
题面:
基本分析:注意剪枝来去重
代码:
class Solution {int[] arr;int len;int t;public List<List<Integer>> combinationSum(int[] candidates, int target) {arr = candidates;List<List<Integer>> list = new ArrayList<>();List<Integer> stack = new Stack<>();len = candidates.length;t = target;Arrays.sort(arr);recursion(list,stack,0,0);return list;}public void recursion(List<List<Integer>> list,List<Integer> stack,int sum,int l){if(sum==t){list.add(new ArrayList<>(stack));return;}for(int i = l;i<len;i++){if(sum+arr[i]>t)return;stack.add(arr[i]);recursion(list,stack,sum+arr[i],i);stack.remove(stack.size()-1);}}
}5.组合总和II
题目链接:40. 组合总和 II - 力扣(LeetCode)
题面:
基本分析:注意重复元素导致的重复,用set是一种解决办法但是会超时
代码:
class Solution {int t;int[] arr;int n;public List<List<Integer>> combinationSum2(int[] candidates, int target) {Arrays.sort(candidates);arr = candidates;Set<List<Integer>> list = new HashSet<>();List<Integer> stack = new ArrayList<>();n = arr.length;t = target;recursion(list,stack,0,0);return new ArrayList<>(list);}public void recursion(Set<List<Integer>> list,List<Integer> stack,int sum,int l){if(sum==t){list.add(new ArrayList<>(stack));return;}for(int i =l;i<n;i++){if(sum+arr[i]>t)return;if (i > l && arr[i] == arr[i - 1]) {continue;}stack.add(arr[i]);recursion(list,stack,sum+arr[i],i+1);stack.remove(stack.size()-1);}}
}后言
上面是回溯算法的基本概念和部分习题,下一篇会讲解回溯算法的其他相关力扣习题,希望有所帮助,一同进步,共勉! 
相关文章:

回溯算法-Java【力扣】【算法学习day.14】
前言 ###我做这类文档一个重要的目的还是给正在学习的大家提供方向(例如想要掌握基础用法,该刷哪些题?)我的解析也不会做的非常详细,只会提供思路和一些关键点,力扣上的大佬们的题解质量是非常非常高滴&am…...

从本地到云端:跨用户请求问题的完美解决方案
对于某些单个请求或响应中含有多个用户信息的服务,SDK提供了一套基于统一的UCS拆分和聚合的解决方案供开发者使用。 请求拆分 对于跨用户服务的请求,我们提供了两个处理方案: 【1】根据用户信息拆分请求: 场景:请求内…...

leetcode day4 409+5
409 最长回文串 给定一个包含大写字母和小写字母的字符串 s ,返回 通过这些字母构造成的 最长的 回文串 的长度。 在构造过程中,请注意 区分大小写 。比如 "Aa" 不能当做一个回文字符串。 示例 1: 输入:s "abccccdd" 输出:7 解…...

英语语法学习框架(考研)
一、简单句 英语都是由简单句构成,简单句共有五种基本句型:①主谓;②主谓宾;③主谓宾宾补;④主谓宾间宾(间接宾语);⑤主系表; 其中谓语是句子最重要的部分,谓…...

基于neo4j的学术论文关系管理系统
正在为毕业设计头疼?又或者在学术研究中总是找不到像样的工具来管理浩瀚的文献资料?今天给大家介绍一款超实用的工具——基于Neo4j的学术论文关系管理系统,让你轻松搞定学术文献的管理与展示!🎉 系统的核心是什么呢&a…...

C#中的委托、匿名方法、Lambda、Action和Func
委托 委托概述 委托是存有对某个方法的引用的一种引用类型变量。定义方法的类型,可以把一个方法当作另一方法的参数。所有的委托(Delegate)都派生自 System.Delegate 类。委托声明决定了可由该委托引用的方法。 # 声明委托类型 委托类型声…...

IDEA关联Tomcat——最新版本IDEA 2024
1.链接Tomcat到IDEA上 添加Tomcat到IDEA上有两种方式: 第一种: (1)首先,来到欢迎界面,找到左侧的Customize选项 (2)然后找到Build、Execution、Deployment选项 (3&am…...

【如何获取股票数据18】Python、Java等多种主流语言实例演示获取股票行情api接口之沪深A股解禁限售数据获取实例演示及接口API说明文档
最近一两年内,股票量化分析逐渐成为热门话题。而从事这一领域工作的第一步,就是获取全面且准确的股票数据。因为无论是实时交易数据、历史交易记录、财务数据还是基本面信息,这些数据都是我们进行量化分析时不可或缺的宝贵资源。我们的主要任…...

NVR小程序接入平台/设备EasyNVR多品牌NVR管理工具/设备的多维拓展与灵活应用
在数字化安防时代,NVR批量管理软件/平台EasyNVR作为一种先进的视频监控系统设备,正逐步成为各个领域监控解决方案的首选。NVR批量管理软件/平台EasyNVR作为一款基于端-边-云一体化架构的国标视频融合云平台,凭借其部署简单轻量、功能多样、兼…...
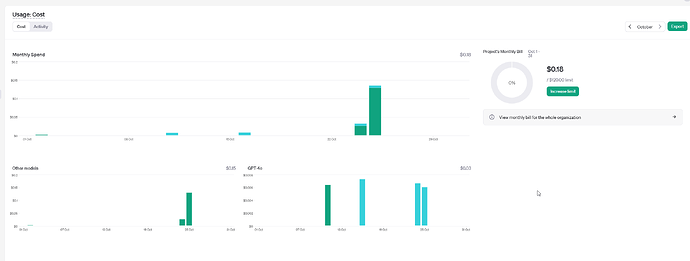
GPT-4o 和 GPT-4 Turbo 模型之间的对比
GPT-4o 和 GPT-4 Turbo 之间的对比 备注 要弄 AI ,不同模型之间的对比就比较重要。 GPT-4o 是 GPT-4 Turbo 的升级版本,能够提供比 GPT-4 Turbo 更多的内容和信息,但成功相对来说更高一些。 第三方引用 在 2024 年 5 月 13 日࿰…...

gin入门教程(10):实现jwt认证
使用 github.com/golang-jwt/jwt 实现 JWT(JSON Web Token)可以有效地进行用户身份验证,这个功能往往在接口前后端分离的应用中经常用到。以下是一个基本的示例,演示如何在 Gin 框架中实现 JWT 认证。 目录结构 /hello-gin │ ├── cmd/ …...

Python 基础语法 - 数据类型
顾名思义,计算机就是用来做数学计算的机器,因此,计算机程序理所当然的可以处理各种数值。但是,计算机能处理的远远不止数值,还可以处理文本,图形,音频,视频,网页等各种各…...
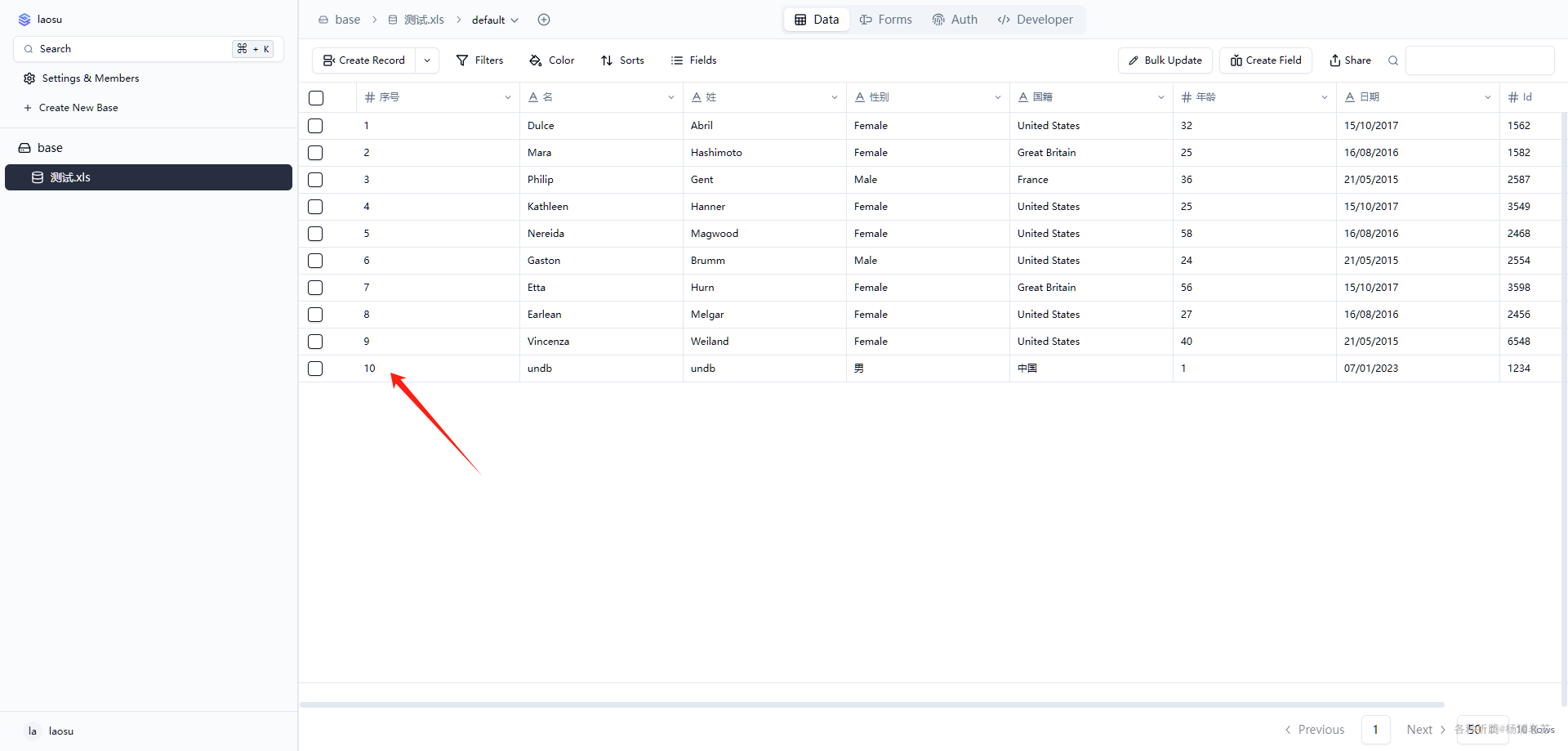
自托管无代码数据库Undb
什么是 Undb ? Undb 是一个无代码平台,也可以作为后端即服务 (BaaS)。它基于 SQLite,可以使用 Bun 打包成二进制文件用于后端服务。此外,它可以通过 Docker 部署为服务,提供表管理的 UI。 软件特点: ⚡ 无…...
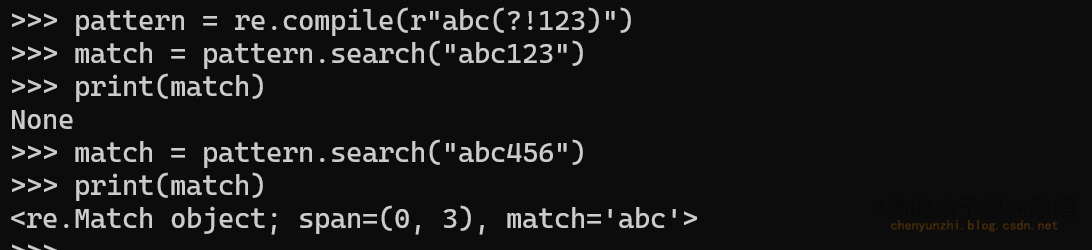
正则的正向前瞻断言和负向前瞻断言
正则的正向前瞻断言和负向前瞻断言 一. 正向前瞻断言二. 负向前瞻断言三. 总结 这是我在这个网站整理的笔记,有错误的地方请指出,关注我,接下来还会持续更新。 作者:神的孩子都在歌唱 正向前瞻断言和负向前瞻断言是正则表达式中用于检查后续字…...
高频面试题及参考答案)
大厂物联网(IoT)高频面试题及参考答案
目录 解释物联网 (IoT) 的基本概念 物联网的主要组成部分有哪些? 描述物联网的基本架构。 IoT 与传统网络有什么区别? 物联网中常用的传感器类型有哪些? 描述物联网的三个主要层次。 简述物联网中数据安全的重要性 描述物联网安全的主要威胁 解释端到端加密在 IoT 中…...

react hook
react hook 最近实习有点忙,所以学习记录没来得及写。 HOC higher order components(HOC) 高阶组件是一个组件,接受一个参数作为组件,返回值也是一个组件的函数。高阶组件作用域强化组件,服用逻辑,提升渲染性能等。…...

Jetpack架构组件_LiveData组件
1.LiveData初识 LiveData:ViewModel管理要展示的数据(VM层类似于原MVP中的P层),处理业务逻辑,比如调用服务器的登陆接口业务。通过LiveData观察者模式,只要数据的值发生了改变,就会自动通知VIEW层…...
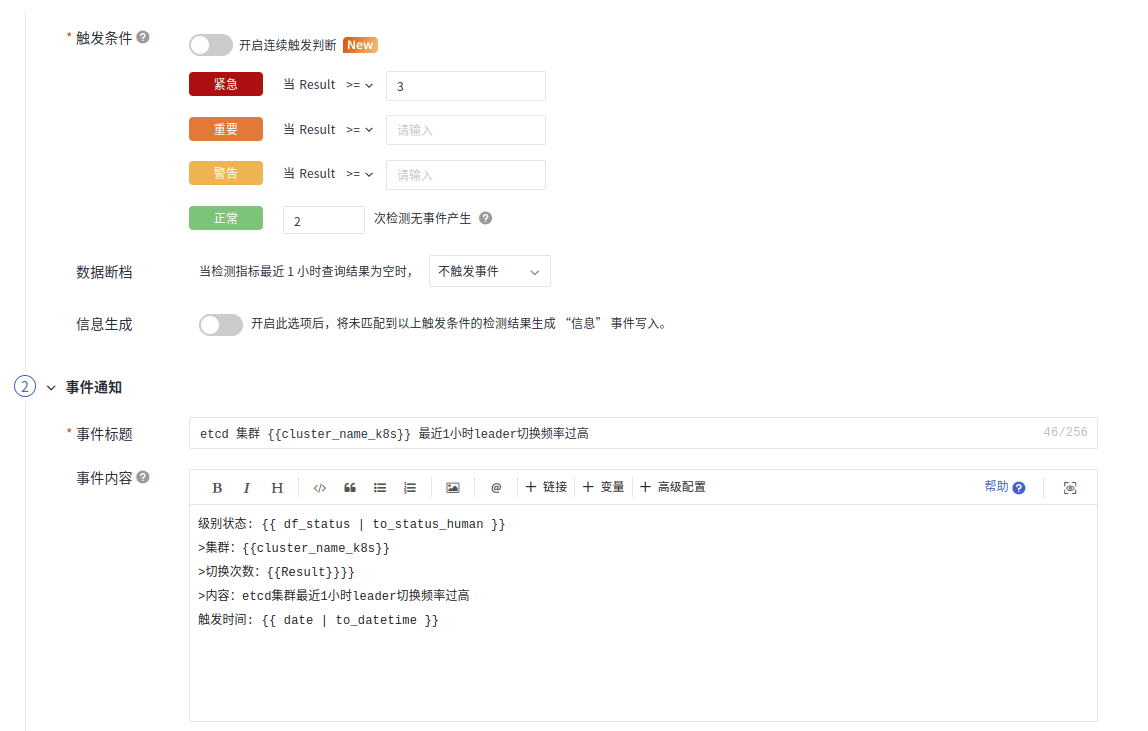
Etcd 可观测最佳实践
简介 Etcd 是一个高可用的分布式键值存储系统,它提供了一个可靠的、强一致性的存储服务,用于配置管理和服务发现。它最初由 CoreOS 开发,现在由 Cloud Native Computing Foundation (CNCF) 维护。Etcd 使用 Raft 算法来实现数据的一致性&…...

钉钉录播抓取视频
爬取钉钉视频 免责声明 此脚本仅供学习参考,切勿违法使用下载他人资源进行售卖,本人不但任何责任! 仓库地址: GItee 源码仓库 执行顺序 poxyM3u8开启代理getM3u8url用于获取m3u8文件userAgent随机请求头downVideo|downVideoThreadTqdm单线程下载和…...

centos下面的jdk17的安装配置
文章目录 1.基本指令回顾2.jdk17的安装到这个centos上面2.1首先切换到这个root下面去2.2查看系统jdk版本2.3首先到官网找到进行下载2.4安装包的上传2.5jdk17的安装包的解压过程2.6配置环境变量2.7是否设置成功,查看版本 1.基本指令回顾 ls:list也就是列出来这个目录…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...
