python单因素分析
写了个简易小程序实现,以后用的时候直接复制就行:
import numpy as np
from scipy.stats import fdatas = [[65,60,69,79,38,68,54,67,68,43],[74,71,58,49,58,49,48,68,56,47],[22,34,24,21,20,36,36,31,28,33]
]
a = 0.05def get_mean_var(data):data_mean = np.mean(data)data_var = np.var(data)return data_mean, data_varn_total = 0
for i in range(len(datas)):print(f'n_{i+1}:{len(datas[i])}')n_total += len(datas[i])print(f'n_total:{len(datas)}')# 求所有data的平方和
data_all = np.concatenate(datas)
data_all_mean, data_all_var = get_mean_var(data_all)total_square_sum = data_all_var*len(data_all)
print(f'总体均值: {data_all_mean}')
# 求组间平方和
group_square_sum = 0
for data in datas:data_mean, _ = get_mean_var(data)group_square_sum += len(data) * (data_mean - data_all_mean)**2# 求误差平方和
error_square_sum = 0
for data in datas:data_mean, _ = get_mean_var(data)for d in data:error_square_sum += (d-data_mean)**2s = len(datas)
n = n_totalA_mean_square_sum = group_square_sum/(s-1)
E_mean_square_sum = error_square_sum/(n-s)
F_value = A_mean_square_sum/E_mean_square_sum
F_threshold = f.isf(q=a,dfn=s-1,dfd=n-s)
# 列表输出
print(f'| 方差来源 | 平方和 | 自由度 | 均方和 | F值 |')
print(f'| 因素A | {group_square_sum} | {s-1} | {A_mean_square_sum} | {F_value}')
print(f'| 误差E | {error_square_sum} | {n-s} | {E_mean_square_sum} |')
print(f'| 总体T | {total_square_sum} | {n-1} |')print(f'\na值: {a}')
print(f'临界F值---F_{a}({s-1},{n-s}): {F_threshold}' )if F_value > F_threshold:print('拒绝原假设,不同处理之间存在显著差异')
else:print('接受原假设,不同处理之间不存在显著差异')
相关文章:

python单因素分析
写了个简易小程序实现,以后用的时候直接复制就行: import numpy as np from scipy.stats import fdatas [[65,60,69,79,38,68,54,67,68,43],[74,71,58,49,58,49,48,68,56,47],[22,34,24,21,20,36,36,31,28,33] ] a 0.05def get_mean_var(data):data_m…...

「C/C++」C++ STL容器库 之 std::list 双向链表容器
✨博客主页何曾参静谧的博客📌文章专栏「C/C」C/C程序设计📚全部专栏「VS」Visual Studio「C/C」C/C程序设计「UG/NX」BlockUI集合「Win」Windows程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「PK」Parasoli…...

应用程序框架进阶<HarmonyOS第一课>
一、判断题 1. 一个应用是由一个或多个HAP组成。 正确(True) 错误(False) 正确(True) 回答正确 2. UIAbility组件多实例启动模式是默认的启动模式。 正确(True)错误(False) 错误(False) 回答正确 二、单选题 1. 以下关于指定实例启动模式说法正确的是? …...

【C++】vector<string>-动态数组存储多个string
#1024程序员节 | 征文# //demo #include <iostream> #include <vector> #include <string>using namespace std; int main() {// 创建一个存储字符串的向量vector<string> Record;// 向向量中添加字符串Record.push_back("example");Record…...
66Analytics 汉化版,网站统计分析源码,汉化前台后台
66Analytics 汉化版,网站统计分析源码,汉化前台后台 本源码汉化前台后台,非其他只汉化前台版 网络分析变得容易。自托管、友好、一体化的网络分析工具。轻量级跟踪、会话回放、热图、用户旅程等 简单、好看、友好-大多数网络分析解决方案做得太多了,在大…...

蓝桥杯单片机STC15F2K60S2第十四届省赛代码详细讲解(附完整代码)
本文是写第十四届的蓝桥杯省赛代码,新手教程作者也写了一篇,欢迎去观看作者专门为新手写的一篇。也欢迎收录该专栏。 蓝桥杯单片机STC15F2K60S2第十三届省赛代码详细讲解(附完整代码) 专栏: 蓝桥杯单片机 然后接下来…...

[免费]SpringBoot+Vue智慧校园(校园管理)系统[论文+源码+SQL脚本]
大家好,我是java1234_小锋老师,看到一个不错的SpringBootVue智慧校园(校园管理)系统,分享下哈。 项目视频演示 【免费】SpringBootVue智慧校园(校园管理)系统 Java毕业设计_哔哩哔哩_bilibili 项目介绍 随着信息技术的迅猛发展,…...
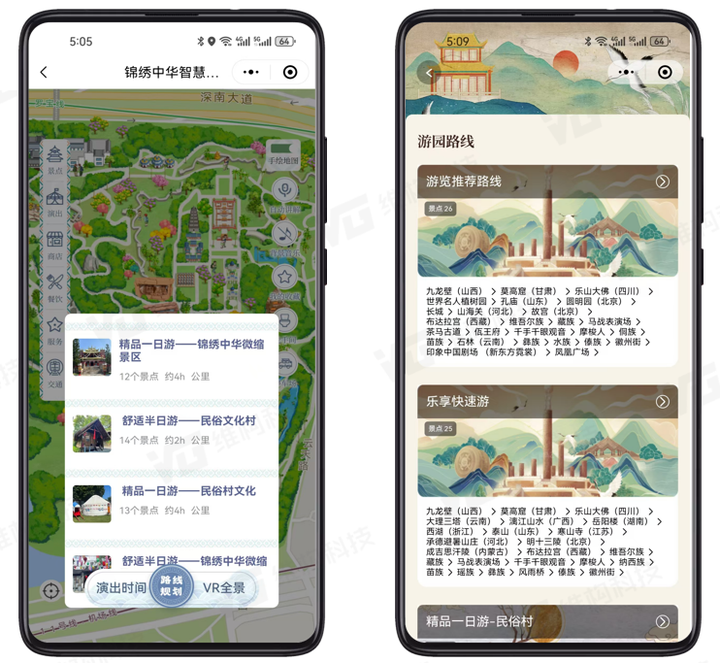
景区导航地图怎么实现?基于LBS与3D GIS的智慧景区导航导览系统技术路线
随着经济的发展和人们物质生活水平改善,居民的旅游需求呈现多元化和个性化,自助旅游的人越来越多。许多游客在旅游行程中需要随时随地了解旅游景点有关的各类信息,如旅游景点介绍、推荐路线、地图导航等,合理规划和安排旅游线路。正是为了应对…...

RedisIO多路复用
一、多路复用要解决的问题: 并发多客户端连接,在多路复用之前的处理方案是同步阻塞网络IO模型,这种模型的特点就是用一个进程来处理一个网络连接。优点在于比较简单,缺点在于性能较差,每个用户请求到来都得占用一个进程来处理&am…...

C++的相关习题(2)
初阶模板 下面有关C中为什么用模板类的原因,描述错误的是? ( ) A.可用来创建动态增长和减小的数据结构 B.它是类型无关的,因此具有很高的可复用性 C.它运行时检查数据类型,保证了类型安全 D.它是平台无关的,可移植…...

C++《vector的模拟实现》
在之前《vector》章节当中我们学习了STL当中的vector基本的使用方法,了解了vector当中各个函数该如何使用,在学习当中我们发现了vector许多函数的使用是和我们之前学习过的string类的,但同时也发现vector当中一些函数以及接口是和string不同的…...

无人机避障——路径规划篇(一) JPS跳点搜索算法A*算法对比
JSP 跳点搜索算法与改进 A*算法对比 一、算法概述: 跳点搜索(Jump Point Search,JPS)算法:一种用于路径规划的启发式搜索算法。它主要用于在网格地图(如游戏地图、机器人运动规划地图等)中快速找到从起点到终点的最短路径。该算法在改进 A*算法的基础上进行了优化,通过跳过一…...

OpenCV ORB角点检测匹配和偏移计算
OpenCV ORB角点检测匹配和偏移计算 1. 简介2. ORB角点检测匹配和偏移计算2.1. 创建平移图片2.2. ORB角点检测2.3. ORB角点匹配2.4. 计算变换矩阵 1. 简介 首先通过 cv2.ORB_create 创建ORB检测器 orb, 然后通过 orb.detectAndCompute 检测两张图片获得ORB角点&…...

图文详解ChatGPT-o1完成论文写作的全流程
学境思源,一键生成论文初稿: AcademicIdeas - 学境思源AI论文写作 本月中旬OpenAI发布了OpenAI o1系列新的AI模型。 据OpenAI介绍,这些模型旨在花更多时间思考后再做出反应,就像人一样。通过训练,它们学会改进思维过…...

在线体验Sketch中文版,免费下载即刻上手!
Sketch是一款轻量而高效的矢量设计工具,助力全球设计师创造了诸多惊艳作品。安装Sketch的优势主要体现在其矢量编辑、控件和样式功能上。而下载安装“Sketch中文版”即时设计同样出色,它作为一站式设计平台,功能更全面。即时设计拥有纯中文的…...

Redis——缓存
目录 前言 一、缓存基本概念 1.概念 2.二八定律 二、使用 Redis 作为缓存 三、缓存的更新策略 1.定期生成 2.实时生成 四、Redis 内存淘汰机制 1.通用淘汰策略 (1)FIFO (2)LRU (3)LFU &#…...
RHCSA笔记三
第二章 linux中执行命令 命令格式 命令分为两类 内置命令:由 shell 程序自带的命令 外部命令:有独立的可执行程序文件,文件名即命令名 格式 主命令 参数 操作对象 # 注意: 下面是对于命令的语法的一些符号的说明࿱…...
 list.sort())
【python】sorted() list.sort()
文章目录 sorted()和list.sort()sorted 函数sorted()根据键对字典排序根据字典的键排序根据字典的值排序将排序结果转换回字典 list.sort() 方法总结 keylambda student: student[age] sorted()和list.sort() 在Python中,sorted 函数和 list.sort() 方法都可以用来…...

训练集alpaca、sharegpt格式
LLaMA-Factory微调支持的格式 支持 alpaca 格式和 sharegpt 格式的数据集。 Alpaca格式 格式: [{"instruction": "人类指令(必填)","input": "人类输入(选填)","output": "模型回答(必填)","syst…...

Hive的数据存储格式
目录 一、前言 二、存储格式 2.1、文本格式(TextFile) 2.1.1、定义与特点 2.1.2、存储与压缩 2. 1.3、使用场景 2.2、行列式文件(ORCFile) 2.2.1、ORC的结构 2.2.2、ORC的数据类型 2.2.3、ORC的压缩格式 2.2.3、ORC存储…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...
