目标跟踪算法-卡尔曼滤波详解

卡尔曼滤波是一种递归的优化算法，用于估计一个系统的动态状态，常用于跟踪、导航、时间序列分析等领域。它的关键在于使用一系列测量数据（通常含噪声）来估计系统的真实状态，使得估计值更接近实际情况。卡尔曼滤波器适合在一维或多维的状态空间中跟踪一个随时间变化的系统状态。

一、卡尔曼滤波器的基本概念

卡尔曼滤波器通过一系列测量数据和预测模型，实时地估计系统的状态。它假设系统具有高斯噪声和线性变化，可以用系统的动态模型和测量模型来描述：

• 动态模型：描述系统状态如何从一个时间点转移到下一个时间点。
• 测量模型：描述测量如何反映当前系统状态。

二、卡尔曼滤波的数学模型

卡尔曼滤波器通过两个关键方程来描述系统的状态：

1. 状态转移方程：描述当前状态由前一状态的转移关系
2. 观测方程：描述测量值如何从当前状态推导而来

假设系统状态向量为 xk，观测值为 zk​，则：

1. 状态转移方程

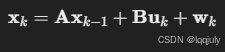
其中：

• A：状态转移矩阵，用于描述系统如何随时间变化。
• B：控制输入矩阵。
• uk：控制向量（可选，通常忽略）。
• wk​：过程噪声，服从高斯分布，协方差为 Q。

2. 观测方程

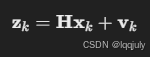
其中：

• H：观测矩阵，描述如何通过状态向量计算观测值。
• vk：测量噪声，服从高斯分布，协方差为 R。

三、卡尔曼滤波器的运算步骤

卡尔曼滤波器主要包括两个阶段：预测和更新。

1. 预测阶段

基于当前状态估计，预测下一时间步的状态和误差协方差。

• 状态预测：
• 误差协方差预测：

2. 更新阶段

一旦获得观测值 zk​，便可以通过更新步骤修正预测值，使估计值更接近真实值。

• 计算卡尔曼增益 Kk​：
• 状态更新：
• 误差协方差更新： ​

其中，Kk称为卡尔曼增益，它决定了对观测值的信任程度。如果测量噪声很小，卡尔曼增益将更高，观测值的影响更大；反之则偏重预测值。

四、卡尔曼滤波的物理意义

• 预测步骤：根据上一步的状态来预测当前状态，主要依赖系统的动态模型。
• 更新步骤：根据测量值修正预测结果，使得估计值更接近真实值。

卡尔曼滤波通过在预测和更新之间进行平衡，使得估计结果具有一定的抗噪能力，尤其在高噪声环境下表现出色。

五、卡尔曼滤波的优缺点

优点：

1. 高效：卡尔曼滤波通过递归计算，能实时处理数据，适用于嵌入式系统。
2. 最优估计：对于线性高斯系统，卡尔曼滤波是最优估计。

缺点：

1. 只适用于线性系统：对于非线性系统，需要扩展卡尔曼滤波（EKF）或无迹卡尔曼滤波（UKF）。
2. 对噪声模型敏感：如果噪声不满足高斯分布，卡尔曼滤波的效果会显著下降。

六、扩展卡尔曼滤波（EKF）和无迹卡尔曼滤波（UKF）

对于非线性系统，卡尔曼滤波可扩展为EKF或UKF。

1. EKF：通过对非线性函数进行一阶线性化来近似计算。
2. UKF：使用一组样本点（称为sigma点）来估计非线性函数的状态分布，更适合高度非线性问题。

七、卡尔曼滤波在多目标跟踪中的应用

在多目标跟踪任务中，如物体检测和行人跟踪等，卡尔曼滤波可以用来预测物体在下一帧的位置，以便在视频中连续识别同一个目标。

1. 预测和匹配

• 使用卡尔曼滤波预测目标的状态，包括位置、速度等信息。
• 在新一帧图像中，通过检测算法识别出目标位置，结合卡尔曼滤波的预测结果进行匹配。

2. 处理遮挡

• 当目标被短暂遮挡时，卡尔曼滤波器仍能提供较准确的预测，待目标再次出现后进行更新。

3. 与深度学习结合

在 DeepSORT 等算法中，卡尔曼滤波与深度学习模型结合，通过深度特征辅助数据关联。DeepSORT的基本流程为：

• 目标检测模块生成检测框。
• 卡尔曼滤波预测每个目标的下一位置。
• 利用检测框和卡尔曼滤波预测位置进行匹配，同时使用深度特征辅助匹配，提高多目标跟踪的准确性。

八、应用案例：一维位置预测

假设我们跟踪一个沿直线运动的目标，每秒测量一次其位置，但测量包含噪声。

1. 状态向量：。
2. 状态转移矩阵：
3. 观测矩阵：

使用卡尔曼滤波，我们可以实时跟踪和预测目标位置，且能在测量误差较大的情况下保持估计的准确性。

九、卡尔曼滤波器来估计物体位置的 Python 示例代码（一维位置预测）

思路：

        # 初始化
        x = 初始状态 # 初始位置和速度
        P = 初始误差协方差 # 通常取较大值
        Q = 过程噪声协方差
        R = 测量噪声协方差
        A = 状态转移矩阵
        H = 观测矩阵

        # 时间步循环
        for k in range(1, N):
           # 1. 预测步骤
            x = A * x  # 状态预测
            P = A * P * A.T + Q  # 协方差预测

            # 2. 更新步骤（使用观测值 z_k）
            K = P * H.T * np.linalg.inv(H * P * H.T + R)  # 卡尔曼增益
            x = x + K * (z_k - H * x)  # 状态更新
            P = (I - K * H) * P  # 协方差更新

import numpy as npclass KalmanFilter:def __init__(self, process_variance, measurement_variance):# 初始值self.x = 0.0  # 初始位置self.P = 1.0  # 初始估计协方差# 过程和测量噪声的协方差self.process_variance = process_variance  # 过程噪声（系统噪声）self.measurement_variance = measurement_variance  # 测量噪声def predict(self, u=0.0):# 预测下一状态self.x = self.x + u  # 这里假设 u 是控制输入，例如速度self.P = self.P + self.process_variance  # 更新预测协方差def update(self, measurement):# 计算卡尔曼增益K = self.P / (self.P + self.measurement_variance)# 更新状态和协方差self.x = self.x + K * (measurement - self.x)  # 更新估计值self.P = (1 - K) * self.P  # 更新估计误差def get_estimate(self):return self.x# 初始化卡尔曼滤波器
process_variance = 1e-5  # 过程噪声越小，滤波器更信任模型
measurement_variance = 0.1  # 测量噪声越大，滤波器更信任预测
kf = KalmanFilter(process_variance, measurement_variance)# 模拟测量数据（实际应用中可以是传感器数据）
measurements = [1.0, 2.0, 1.2, 2.1, 2.5, 3.0, 2.8, 3.2, 3.1]# 使用卡尔曼滤波器来平滑这些测量数据
for measurement in measurements:kf.predict()  # 预测步骤kf.update(measurement)  # 更新步骤print(f"测量值: {measurement}, 卡尔曼估计值: {kf.get_estimate()}")