双曲函数(Hyperbolic functuons)公式
在python等语言里有双曲函数库和反双曲函数库,但是并没有包含所有的双曲函数。以numpy为例子,numpy只提供了sinh、cosh、tanh、arcsinh、arccosh、arctanh六种函数,那么其余的就需要用公式计算了。
转换公式
对于函数库不能直接计算的,我整理出了计算公式:
coth x = 1 tanh x s e c h x = 1 cosh x c s c h x = 1 sinh x a r c c o t h x = a r c t a n ( 1 x ) a r c s e c h x = a r c c o s ( 1 x ) a r c c s c h x = a r c s e c ( 1 x ) \coth x = \frac1{\tanh x} \\ sech\thinspace x = \frac1{\cosh x} \\ csch\thinspace x = \frac1{\sinh x} \\ arccoth\thinspace x = arctan (\frac1x)\\ arcsech\thinspace x = arccos (\frac1x)\\ arccsch\thinspace x = arcsec(\frac1x) cothx=tanhx1sechx=coshx1cschx=sinhx1arccothx=arctan(x1)arcsechx=arccos(x1)arccschx=arcsec(x1)
导数公式
对双曲函数和反双曲函数求导的公式也非常重要,必须要背诵下来。
d d x ( sinh x ) = cosh x d d x ( cosh x ) = sinh x d d x ( tanh x ) = s e c h 2 x d d x ( coth x ) = − c s c h 2 x d d x ( s e c h x ) = − s e c h x t a n h x d d x ( c s c h x ) = − c s c h x c o t h x \frac{d}{dx}(\sinh x)=\cosh x\\ \frac{d}{dx}(\cosh x)=\sinh x\\ \frac{d}{dx}(\tanh x)=sech^2\thinspace x\\ \frac{d}{dx}(\coth x)=-csch^2\thinspace x\\ \frac{d}{dx}(sech x)= -sech\thinspace x \thinspace tanh\thinspace x\\ \frac{d}{dx}(csch x)= -csch\thinspace x \thinspace cot h\thinspace x\\ dxd(sinhx)=coshxdxd(coshx)=sinhxdxd(tanhx)=sech2xdxd(cothx)=−csch2xdxd(sechx)=−sechxtanhxdxd(cschx)=−cschxcothx
接下来是反双曲函数inverse hyperbolic functions的导数公式:
d d x ( a r c s i n h x ) = 1 x 2 + 1 d d x ( a r c c o s h x ) = 1 x 2 − 1 , x > 1 d d x ( a r c t a n h x ) = 1 1 − x 2 d d x ( a r c c o t h x ) = 1 1 − x 2 d d x ( a r c s e c h x ) = − 1 x 1 − x 2 d d x ( a r c c o s h x ) = − 1 ∣ x ∣ 1 + x 2 \frac{d}{dx}(arcsinh \thinspace x)=\frac1{\sqrt{x^2+1}}\\ \frac{d}{dx}(arccosh \thinspace x)=\frac1{\sqrt{x^2-1}},x > 1\\ \frac{d}{dx}(arctanh \thinspace x)=\frac1{{1-x^2}}\\ \frac{d}{dx}(arccoth \thinspace x)=\frac1{{1-x^2}}\\ \frac{d}{dx}(arcsech \thinspace x)=-\frac1{x\sqrt{1-x^2}}\\ \frac{d}{dx}(arccosh \thinspace x)=-\frac1{|x|\sqrt{1+x^2}}\\ dxd(arcsinhx)=x2+11dxd(arccoshx)=x2−11,x>1dxd(arctanhx)=1−x21dxd(arccothx)=1−x21dxd(arcsechx)=−x1−x21dxd(arccoshx)=−∣x∣1+x21
积分公式
上面这些求导公式,反推一下就是积分公式了,但是有些特殊的积分公式,不能直接推导出来,需要记忆:
∫ d x a 2 + x 2 = a r c s i n h ( x a ) + C , a > 0 ∫ d x x 2 − a 2 = a r c c o s h ( x a ) + C , x > a > 0 ∫ d x a 2 − x 2 = { 1 a a r c t a n h ( x a ) + C , x 2 < a 2 1 a a r c c o t h ( x a ) + C , x 2 > a 2 ∫ d x x a 2 − x 2 = − 1 a a r c s e c h ( x a ) + C , 0 < x < a ∫ d x x a 2 + x 2 = − 1 a a r c c s c h ∣ x a ∣ + C , x ≠ 0 , a > 0 \int\frac{dx}{\sqrt{a^2+x^2}}= arcsinh \thinspace (\frac{x}{a})+C,a>0\\ \int\frac{dx}{\sqrt{x^2-a^2}}= arccosh \thinspace (\frac{x}{a})+C,x>a>0\\ \int\frac{dx}{a^2-x^2}= \begin{cases} \frac1a \thinspace arctanh \thinspace (\frac{x}{a})+C,x^2<a^2\\ \frac1a \thinspace arccoth \thinspace (\frac{x}{a})+C,x^2>a^2\\ \end{cases}\\ \int\frac{dx}{x\sqrt{a^2-x^2}}=-\frac1a arcsech \thinspace (\frac{x}{a})+C,0<x<a\\ \int\frac{dx}{x\sqrt{a^2+x^2}}=-\frac1a arccsch \thinspace \lvert \frac{x}{a}\rvert+C,x \neq 0, a>0 ∫a2+x2dx=arcsinh(ax)+C,a>0∫x2−a2dx=arccosh(ax)+C,x>a>0∫a2−x2dx={a1arctanh(ax)+C,x2<a2a1arccoth(ax)+C,x2>a2∫xa2−x2dx=−a1arcsech(ax)+C,0<x<a∫xa2+x2dx=−a1arccsch∣ax∣+C,x=0,a>0
恒等式
最后,我再整理一点恒等式:
c o s h 2 x − s i n h 2 x = 1 s i n h x = 2 s i n h x c o s h x c o s h x = s i n h 2 x + c o s h 2 x c o s h 2 x = c o s h 2 x + 1 2 s i n h 2 x = c o s h 2 x − 1 2 t a n h 2 x = 1 − s e c h 2 x c o t h 2 x = 1 + c s c h 2 x cosh^2 \thinspace x -sinh^2 \thinspace x = 1\\ sinh\thinspace x = 2sinh\thinspace x \thinspace cosh\thinspace x \\ cosh\thinspace x = sinh^2\thinspace x \thinspace + cosh^2\thinspace x \\ cosh^2\thinspace x = \frac{cosh\thinspace 2x +1}2\\ sinh^2\thinspace x = \frac{cosh\thinspace 2x -1}2\\ tanh^2\thinspace x = 1-sech^2x\\ coth^2\thinspace x = 1+csch^2x\\ cosh2x−sinh2x=1sinhx=2sinhxcoshxcoshx=sinh2x+cosh2xcosh2x=2cosh2x+1sinh2x=2cosh2x−1tanh2x=1−sech2xcoth2x=1+csch2x
相关文章:
公式)
双曲函数(Hyperbolic functuons)公式
在python等语言里有双曲函数库和反双曲函数库,但是并没有包含所有的双曲函数。以numpy为例子,numpy只提供了sinh、cosh、tanh、arcsinh、arccosh、arctanh六种函数,那么其余的就需要用公式计算了。 转换公式 对于函数库不能直接计算的&#…...

【CSS/SCSS】@layer的介绍及使用方法
目录 基本用法layer 的作用与优点分离样式职责,增强代码可读性和可维护性防止无意的样式冲突精确控制样式的逐层覆盖提高复用性 兼容性实际示例:使用 import 管理加载顺序实际示例:混入与 layer 结合使用 layer 是 CSS 中用于组织和管理样式优…...

我为什么投身于青少年AI编程?——打造生态圈(三)
第五部分 青少年AI编程生态圈 一、生态圈 主要涵盖家庭、社区/中小学、高校高职、主管部门。 1、家庭 我们与社区/中小学一道打造让家长满意的模式。 教得好: 费用少: 家门口: 2、社区/中小学 社区党群服务中心和中小学都有大面积科普…...

出海要深潜,中国手机闯关全球化有了新标杆
经济全球化的大势之下,中国科技企业开拓海外市场已成为一种必然选择。 对于国内手机企业来说,推进全球商业版图扩张,业务潜力巨大,海外市场是今后的关键增长引擎。 当前中国手机厂商在海外市场的发展,有收获也有坎坷…...

百度SEO中的关键词密度与内容优化研究【百度SEO专家】
大家好,我是百度SEO专家(林汉文),在百度SEO优化中,关键词密度和关键词内容的优化对提升页面排名至关重要。关键词的合理布局与内容的质量是确保网页在百度搜索结果中脱颖而出的关键因素。下面我们将从关键词密度和关键…...

如何用fastapi集成pdf.js 的viewer.html ,并支持 mjs
fastapi 框架 集成pdf.js 的 viewer.html?file=***,支持跨域,支持.mjs .wasm .pdf 给出完整示例代码 要在 FastAPI 框架中集成 pdf.js 的 viewer.html,并支持跨域访问以及 .mjs、.wasm、.pdf 文件的正确加载,可以按照以下步骤进行。下面提供一个完整的示例,包括项目结构…...

文件相对路径与绝对路径
前言: 在写代码绘制图像的过程中,发现出现cant read input file的异常,而且输出框没有绘制图片,所以寻找解决方案。先贴上之前写的简洁版绘制图像代码 1.BackGround类 import java.awt.image.BufferedImage;public class BackG…...

Linux 重启命令全解析:深入理解与应用指南
Linux 重启命令全解析:深入理解与应用指南 在 Linux 系统中,掌握正确的重启命令是确保系统稳定运行和进行必要维护的关键技能。本文将深入解析 Linux 中常见的重启命令,包括功能、用法、适用场景及注意事项。 一、reboot 命令 功能简介 re…...

【北京迅为】《STM32MP157开发板嵌入式开发指南》-第六十七章 Trusted Firmware-A 移植
iTOP-STM32MP157开发板采用ST推出的双核cortex-A7单核cortex-M4异构处理器,既可用Linux、又可以用于STM32单片机开发。开发板采用核心板底板结构,主频650M、1G内存、8G存储,核心板采用工业级板对板连接器,高可靠,牢固耐…...

`a = a + b` 与 `a += b` 的区别
在 Java 中,a a b 和 a b 都用于将 b 的值加到 a 上,但它们之间存在一些重要的区别,尤其是在类型转换和操作行为方面。 使用 操作符时,Java 会自动进行隐式类型转换,而使用 则不会。这意味着在 a b 的情况下&am…...

mysqld.log文件过大,清理后不改变所属用户
#1024程序员节# 一、背景 突然有一天,我的mysql报磁盘不足了。仔细查看才发现,是磁盘满了。而MySQL的日志文件占用了91个G.如下所示: [roothost-172-16-14-128 mysql]# ls -lrth 总用量 93G -rw-r----- 1 mysql mysql 1.1G 7月 30 2023 m…...
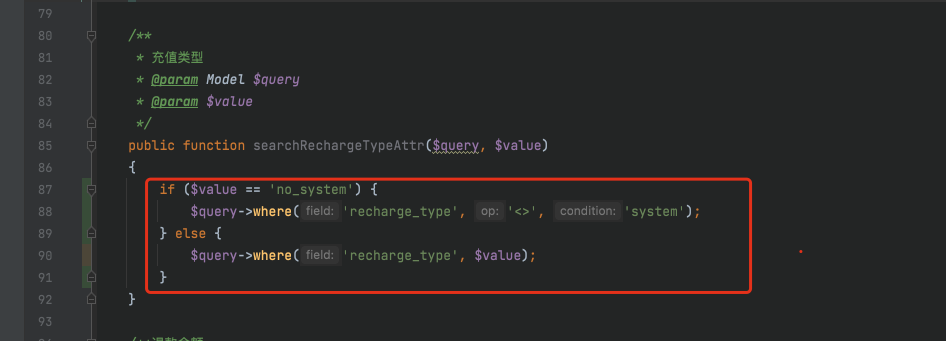
v4.7+版本用户充值在交易统计中计算双倍的问题修复
app/services/statistic/TradeStatisticServices.php 文件中 $whereInRecharge[recharge_type] no_system; $whereInRecharge[recharge_type] system; app/model/user/UserRecharge.php 中 修改此搜索器内容 public function searchRechargeTypeAttr($query, $value){ if…...

[GXYCTF 2019]Ping Ping Ping 题解(多种解题方式)
知识点: 命令执行 linux空格绕过 反引号绕过 变量绕过 base64编码绕过 打开页面提示 "听说php可以执行系统函数?我来康康" 然后输入框内提示输入 bjut.edu.cn 输入之后回显信息,是ping 这个网址的信息 输入127.0.0.1 因为提示是命令…...

MODSI EVI 数据的时间序列拟合一阶谐波模型
目录 简介 函数 ee.Reducer.linearRegression(numX, numY) Arguments: Returns: Reducer ee.Image.cat(var_args) Arguments: Returns: Image hsvToRgb() Arguments: Returns: Image 代码 结果 简介 MODIS/006/MOD13A1数据是由美国国家航空航天局(NASA)的MODIS…...

Java:String类(超详解!)
一.常用方法 🥏1.字符串构造 字符串构造有三种方法: 📌注意: 1. String是引用类型,内部并不存储字符串本身 如果String是一个引用那么s1和s3应该指向同一个内容,s1和s2是相等的,应该输出两…...

【日志】力扣13.罗马数字转整数 || 解决泛型单例热加载失败问题
2024.10.28 【力扣刷题】 13. 罗马数字转整数 - 力扣(LeetCode)https://leetcode.cn/problems/roman-to-integer/description/?envTypestudy-plan-v2&envIdtop-interview-150这题用模拟的思想可以给相应的字母赋值,官方的答案用的是用一…...

Mybatis高级
系列文章目录 高级Mybatis,一些结果映射,引入新的注解 目录 系列文章目录 文章目录 一、结果映射 1.ResultType 2.ResultMap 基础应用: 二、一对一 嵌套结果和嵌套查询 嵌套结果 嵌套查询 区别 三、一对多 四、多对多 五、注解补充 1.一对一…...

【spark】spark structrued streaming读写kafka 使用kerberos认证
spark版本:2.4.0 官网 Spark --files使用总结 Spark --files理解 一、编写jar import org.apache.kafka.clients.CommonClientConfigs import org.apache.kafka.common.config.SaslConfigs import org.apache.spark.sql.SparkSession import org.apache.spark.sql.streaming.T…...

【脚本】B站视频AB复读
控制台输入如下代码,回车 const video document.getElementsByTagName("video")[0];//获取bpx-player-control-bottom-center容器,更改其布局方式const div document.getElementsByClassName("bpx-player-control-bottom-center")[0];div.sty…...
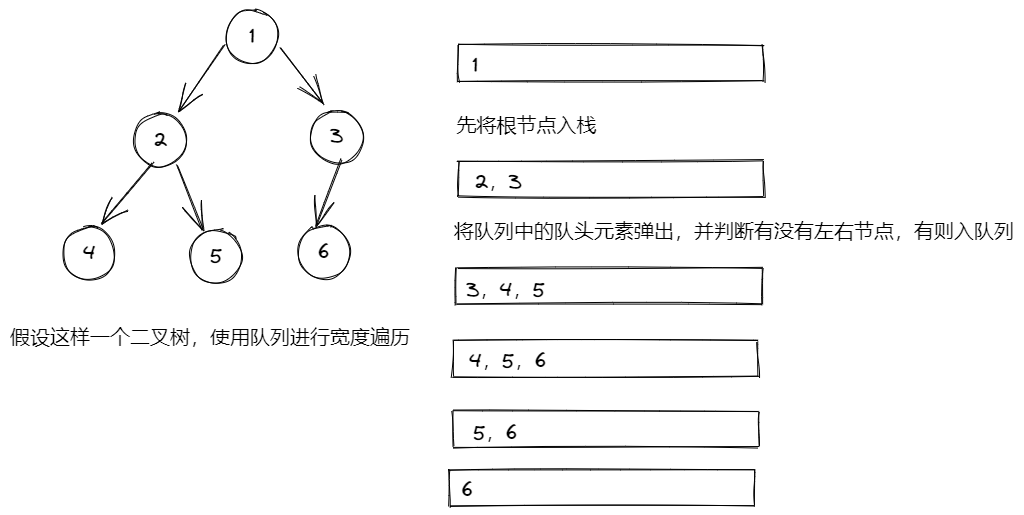
leetcode - 257. 二叉树的所有路径
257. 二叉树的所有路径 题目 解决 做法一:深度优先搜索 回溯 深度优先搜索(Depth-First Search, DFS)是一种用于遍历或搜索树或图的算法。这种搜索方式会尽可能深地探索每个分支,直到无法继续深入为止,然后回溯到上…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...
