【Linux】nohup 命令
【Linux】nohup 命令
- 1. 语法格式
- 2. 实例
- 3. 查找后台进程
nohup 英文全称 no hang up(不挂起),用于在系统后台不挂断地运行命令,退出终端不会影响程序的运行。
nohup 命令,在默认情况下(非重定向时),会输出一个名叫 nohup.out 的文件到当前目录下,如果当前目录的 nohup.out 文件不可写,输出重定向到 $HOME/nohup.out 文件中。
1. 语法格式
nohup Command [ Arg … ] [ & ]
参数说明:
Command:要执行的命令。
Arg:一些参数,可以指定输出文件。
&:让命令在后台执行,终端退出后命令仍旧执行。
2. 实例
以下命令在后台执行 root 目录下的 runoob.sh 脚本:
nohup /root/runoob.sh &
在终端如果看到以下输出说明运行成功:
appending output to nohup.out
这时我们打开 root 目录 可以看到生成了 nohup.out 文件。
以下命令在后台执行 root 目录下的 runoob.sh 脚本,并重定向输入到 runoob.log 文件:
nohup /root/runoob.sh > runoob.log 2>&1 &
2>&1 解释:
将标准错误 2 重定向到标准输出 &1 ,标准输出 &1 再被重定向输入到 runoob.log 文件中。
- 0 – stdin (standard input,标准输入)
- 1 – stdout (standard output,标准输出)
- 2 – stderr (standard error,标准错误输出)
3. 查找后台进程
如果要停止运行,你需要使用以下命令查找到 nohup 运行脚本到 PID,然后使用 kill 命令来删除:
ps -aux | grep "runoob.sh"
参数说明:
a : 显示所有程序
u : 以用户为主的格式来显示
x : 显示所有程序,不区分终端机
另外也可以使用 ps -def | grep "runoob.sh" 命令来查找。
找到 PID 后,就可以使用 kill PID 来删除。
kill -9 进程号PID
也可以使用jobs命令,查看后台进程

相关文章:

【Linux】nohup 命令
【Linux】nohup 命令 1. 语法格式2. 实例3. 查找后台进程 nohup 英文全称 no hang up(不挂起),用于在系统后台不挂断地运行命令,退出终端不会影响程序的运行。 nohup 命令,在默认情况下(非重定向时&#x…...

CSS、Less、Scss
CSS、Less和SCSS都是用于描述网页外观的样式表语言,但它们各自具有不同的特点和功能。以下是对这三者的详细阐述及区别对比: 详细阐述 CSS(Cascading Style Sheets) 定义:CSS是一种用来表现HTML或XML等文件样式的计算机…...

[笔记] ffmpeg docker编译环境搭建
文章目录 环境参考dockerfile 文件步骤常见问题docker 构建镜像出现 INTERNAL_ERROR 失败? 总结 环境 docker 环境 系统centos 7.9 (无所谓了 你用docker编译就无所谓系统了) ffmpeg3.3 参考 https://blog.csdn.net/jiedichina/article/details/71438112 dockerfile 文件 …...

基于SSM的心理咨询管理管理系统(含源码+sql+视频导入教程+文档+PPT)
👉文末查看项目功能视频演示获取源码sql脚本视频导入教程视频 1 、功能描述 基于SSM的心理咨询管理管理系统拥有三个角色:学生用户、咨询师、管理员 管理员:学生管理、咨询师管理、文档信息管理、预约信息管理、测试题目管理、测试信息管理…...

南开大学《2023年+2022年810自动控制原理真题》 (完整版)
本文内容,全部选自自动化考研联盟的:《南开大学810自控考研资料》的真题篇。后续会持续更新更多学校,更多年份的真题,记得关注哦~ 目录 2023年真题 2022年真题 Part1:2023年2022年完整版真题 2023年真题 2022年真题…...

【算法】Kruskal最小生成树算法
目录 一、最小生成树 二、Kruskal算法求最小生成树 三、代码 一、最小生成树 什么是最小生成树? 对于一个n个节点的带权图,从中选出n-1条边(保持每个节点的联通)构成一棵树(不能带环),使得…...

Pocket通常指的是一种特定的凹形或凹槽
在几何和计算机辅助设计(CAD)中,“Pocket”通常指的是一种特定的凹形或凹槽,用于表示在物体表面上挖出的区域。其主要特点包括: 凹形区域:Pocket 是一个在三维模型中内凹的区域,通常从物体的表面…...

Cesium基础-(Entity)-(Billboard)
里边包含Vue、React框架代码 2、Billboard 广告牌 Cesium中的Billboard是一种用于在3D场景中添加图像标签的简单方式。Billboard提供了一种方法来显示定向的2D图像,这些图像通常用于表示简单的标记、符号或图标。以下是对Billboard的详细解读: 1. Billboard的定义和特性 B…...

从0到1,解读安卓ASO优化!
大家好,我是互金行业的一名ASO运营专员,目前是负责我们两个APP的ASO方面的维护,今天分享的内容主要是关于安卓ASO优化方案。 大致内容分为三块: 首先我要讲一下ASO是什么;接下来就是安卓的渠道的选择,安卓…...

go语言中流程控制语句
Go语言中的流程控制语句包括条件判断、循环和分支控制。以下是详细介绍: 1. 条件判断语句 if 语句 Go语言的 if 语句与其他语言类似,支持基本的条件判断。 if 条件 {// 执行代码 }if-else 语句: if 条件 {// 执行代码 } else {// 执行代码…...

k8s 部署 emqx
安装cert-manager 使用Helm安装 helm repo add jetstack https://charts.jetstack.io helm repo update helm upgrade --install cert-manager jetstack/cert-manager \--namespace cert-manager \--create-namespace \--set installCRDstrue如果通过helm命令安装失败&#x…...

CSS.导入方式
1.内部样式 在head的style里面定义如 <style>p1{color: brown;}</style> 2.内联样式 直接在标签的里面定义如 <p2 style"color: blue;">这是用了内联样式,蓝色</p2><br> 3.外部样式表 在css文件夹里面构建一个css文件…...

Linux之nfs服务器和dns服务器
NFS服务器 NFS(Network File System,网络文件系统),NFS服务器可以让PC将网络中的NFS服务器共享的目录挂载到本地端的文件系统中,而在本地端的系统 中看来,那个远程主机的目录就好像是自己的一个磁盘分区一样。 注&am…...

大模型系列——AlphaZero/强化学习/MCTS
AlphaGo Zero无需任何人类历史棋谱,仅使用深度强化学习,从零开始训练三天的成就已远远超过了人类数千年积累的围棋知识。 1、围棋知识 (1)如何简单理解围棋知识 (2)数子法分胜负:https://zhu…...
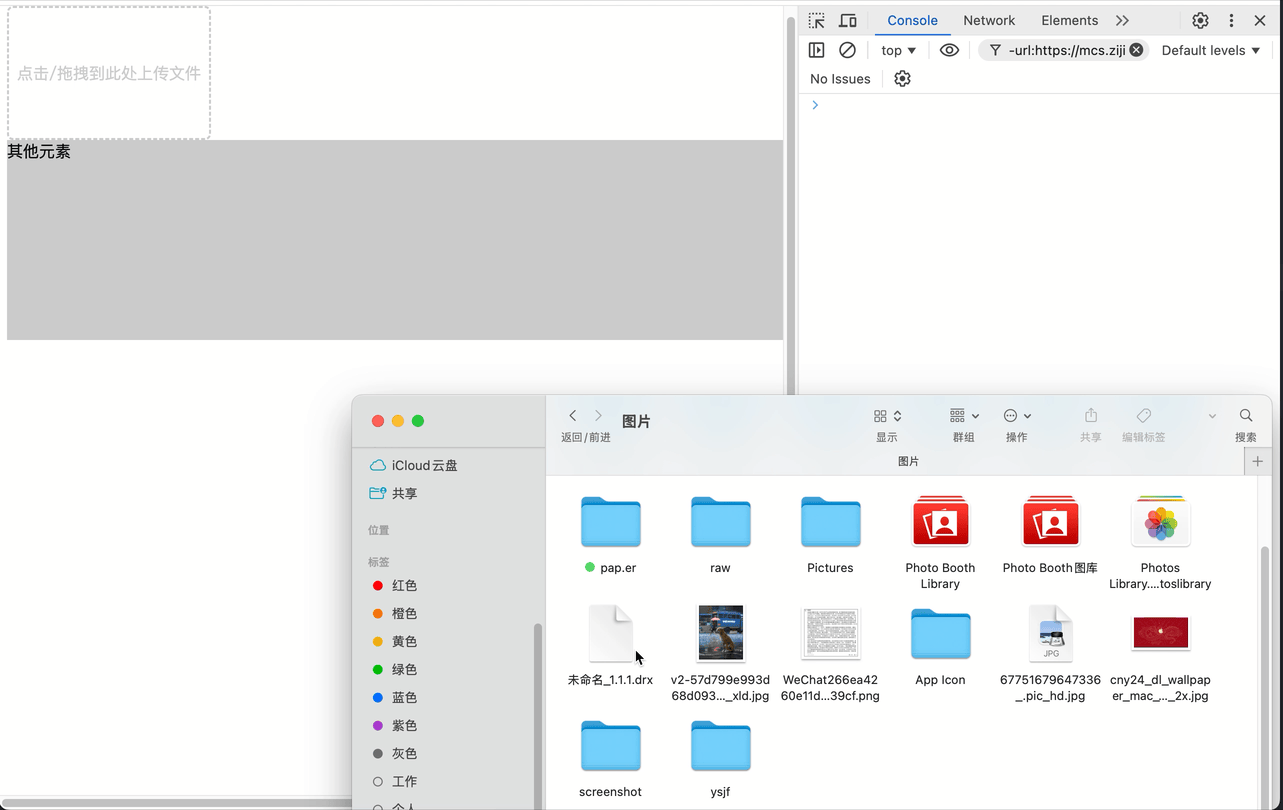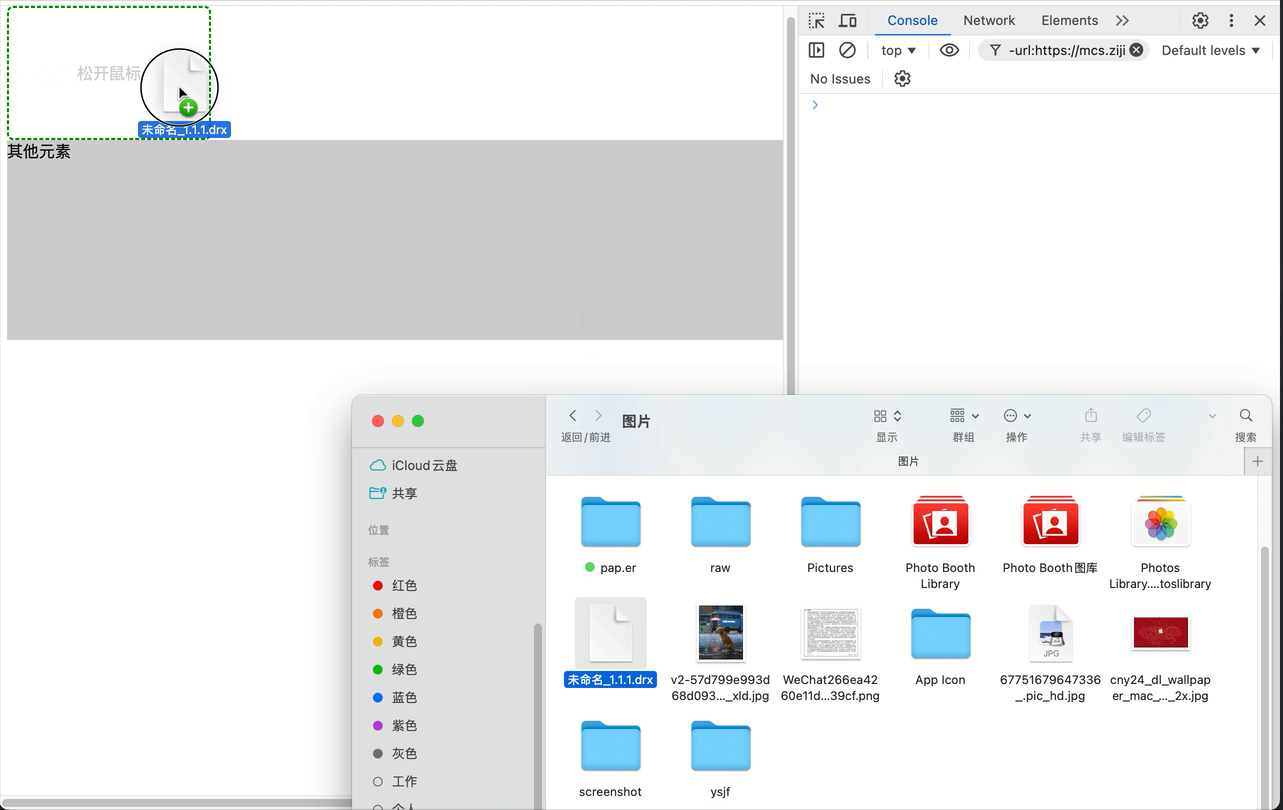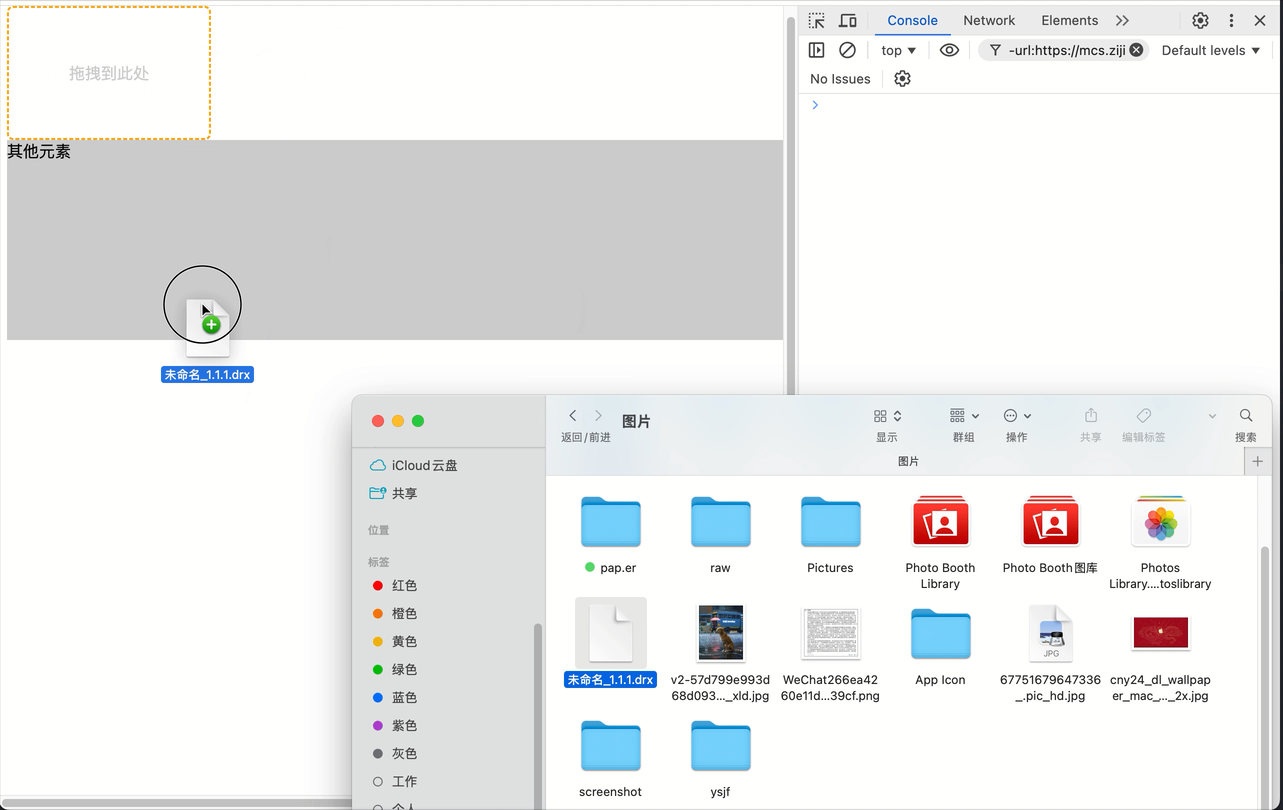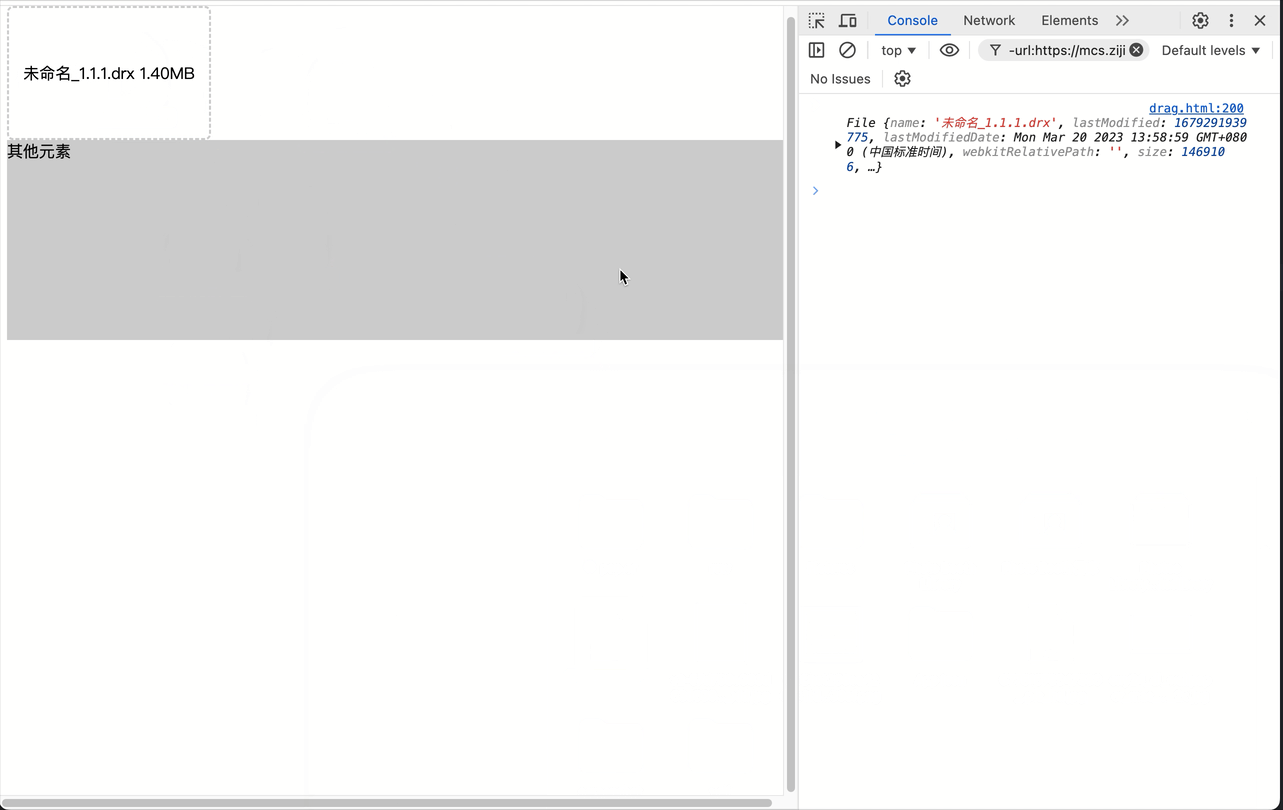
原生js实现拖拽上传(拖拽时高亮上传区域)
文章目录 drop相关事件说明-MDN演示代码(.html) drop相关事件说明-MDN 演示 代码(.html) <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"…...

python道格拉斯算法的实现
废话不多说 直接开干 需要用到模块 pip install -i https://pypi.tuna.tsinghua.edu.cn/simple math #对浮点数的数学运算函数 pip install -i https://pypi.tuna.tsinghua.edu.cn/simple shapely #提供几何形状的操作和分析,如交集、并集、差集等 pip install -i …...

STM32的hal库中,后缀带ex和不带的有什么区别
在STM32的HAL(硬件抽象层)库中,后缀带“ex”和不带“ex”的文件及其包含的内容存在显著的区别。这些区别主要体现在功能扩展性、使用场景以及API的层次上。 一、功能扩展性 不带“ex”后缀的文件: 这些文件通常包含标准的、核心…...

可观测性三大支柱
目录 可观测性成熟度模型 可观测性三大支柱的具体定义如下 指标 日志 链路 可观测性成熟度模型 可观测性成熟度模型,是一种用于衡量和评估企业软件系统内部可观测性的框架或方法,同 时也是一种用于反馈企业可观测性体系建设成熟度水平的框架或方法…...

【银河麒麟高级服务器操作系统·实例分享】裸金属服务器开机失败分析及处理建议
了解更多银河麒麟操作系统全新产品,请点击访问 麒麟软件产品专区:https://product.kylinos.cn 开发者专区:https://developer.kylinos.cn 文档中心:https://documentkylinos.cn 现象描述 裸金属物理服务器开机卡在EFI stub页面…...

模型剪枝实操
文章目录 实验报告:模型剪枝在图像分类任务中的应用摘要实验方法数据集和预处理模型架构剪枝过程实验设置 实验效果性能对比详细分析 结论 实验报告:模型剪枝在图像分类任务中的应用 摘要 本实验通过模型剪枝技术,对一个图像分类模型进行压…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
